
Кристаллография / kristalka
.pdf
Лекция 6. Простые формы, категории, кристаллические системы и сингонии, правила установки и главные направления.
Правильные системы плоскостей и направлений, простые формы
Возьмем некоторое направление в кристаллической среде. Рассматривая действие всех элементов симметрии класса симметрии на это направление, мы получаем множество направлений, симметричных исходному направлению. Все эти направления эквивалентны и неотличимы в том смысле, что произвольные свойства кристаллов в этих направлениях идентичны. Множество эквивалентных направлений в кристалле образуют правильную систему направлений. Число направлений в одной правильной системе направлений называется кратностью правильной системы направлений.
Кратность правильной системы определяется, прежде всего, набором и взаимным расположением элементов симметрии, или, то же, классом симметрии. Кроме того, существенно расположение рассматриваемого направления относительно элементов симметрии. Ясно, что элемент симметрии не действует на параллельное ему направление, и в этом случае кратность правильной системы направлений будет понижена. С этой точки зрения различают правильные системы направлений общего положения, когда направления, входящие в правильную систему, не совпадают с элементами симметрии и правильные системы направлений частного положения, когда направления правильной системы совпадают хотя бы с одним элементом симметрии.
Все вышесказанное можно с равным успехом отнести и к кристаллографическим плоскостям. Взяв некоторую фиксированную плоскость и подействовав на нее элементами симметрии класса симметрии, мы получаем правильную систему плоскостей, число плоскостей в правильной системе называется кратностью. Существенно, что плоскости образуют грани кристалла, а симметричные плоскости – грани с одинаковыми свойствами, например, свойствами роста. Существенно при этом , что знание элементов симметрии позволяет смоделировать все возможные идеальные формы кристалла, которые получаются при огранке плоскостями одной правильной системы. Такие идеальные формы называют простыми формами. Интерактивные модели простых форм можно найти на сайте http://www.ggd.nsu.ru/Crystal/prform.html. Наиболее полно симметрию кристалла отражают многогранники с гранями общего положения. Виды и названия правильных многогранников приведены в таблице.
Простая форма |
|
Наименование |
|
|
|
|
|
Моноэдр |
|
|
|

Пинакоид
Диэдр плоскостной
Диэдр осевой
Ромбическая
пирамида

Ромбическая призма
Ромбический
тетраэдр
Ромбическая
дипирамида
Тригональная
призма
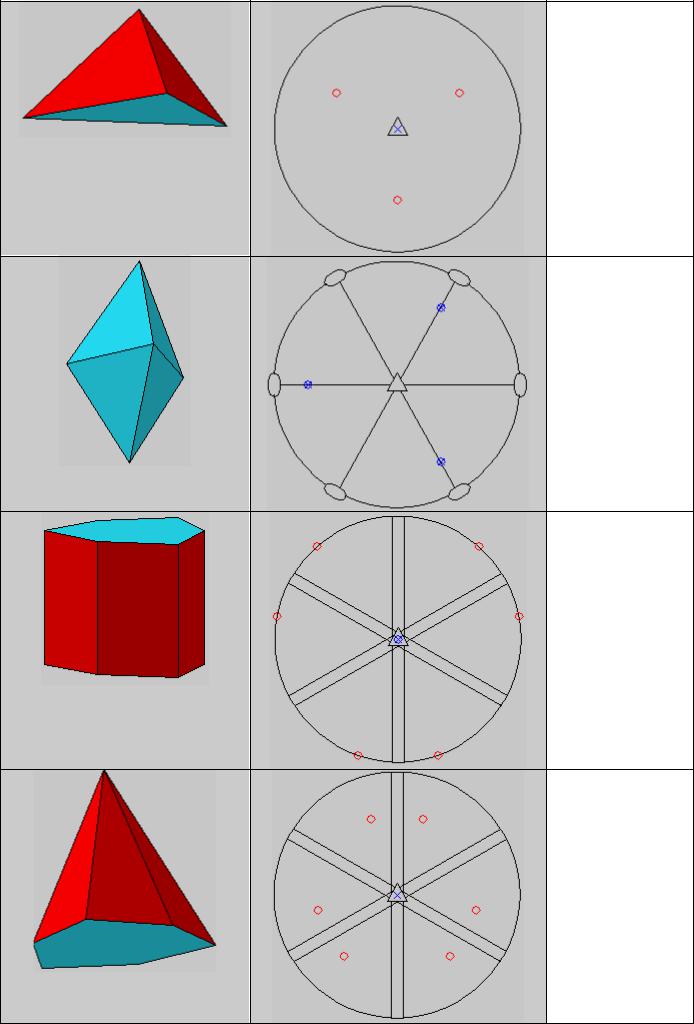
Тригональная
пирамида
Тригональная
бипирамида
Дитригональная
призма
Дитригональная
пирамида

Дитригональная
бипирамида
Тетрагональная
призма
Тетрагональная
пирамида
Тетрагональная
бипирамида

Дитетрагональная
призма
Дитетрагональная
пирамида
Дитетрагональная
бипирамида
Гексагональная
призма

Гексагональная
пирамида
Гексагональная
бипирамида
Дигексагональная
призма
Дигексагональная
пирамида

Дигексагональная
бипирамида
Тригональный
трапецоэдр
Тетрагональный
трапецоэдр
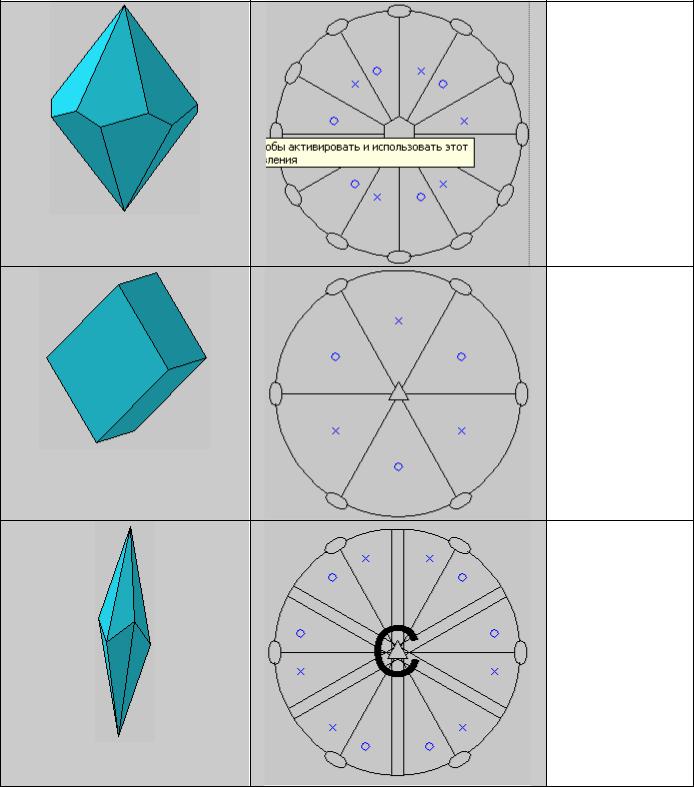
Гексагональный
трапецоэдр
Ромбоэдр
Тригональный
скаленоэдр

Тетрагональный
скаленоэдр
Тетраглналдьный
тетраэдр
Тетраэдр
