Лекции / ЛЕКЦИЯ 3.doc Дискретный источник

ЛЕКЦИЯ 3

ДИСКРЕТНЫЙ ИСТОЧНИК. ОСНОВНАЯ ТЕОРЕМА К. ШЕННОНА ДЛЯ ДИСКРЕТНОГО КАНАЛА БЕЗ ШУМА.

ЦЕЛЬ ЛЕКЦИИ: Дать определение и характеристику дискретного источника, определить энтропию источника, доказать, что при заданных ограничениях всегда можно сформировать последовательность символов, энтропия которой будет сколь угодно близка к энтропии источника, что, в свою очередь, позволяет при использовании статистического кодирования максимально использовать пропускную способность канала связи.

В предыдущей лекции было приведено определение источника сообщений как источника, который может в каждый момент времени с некоторой вероятностью принять одно из конечного множества возможных состояний. Источник, принимающий возможные вероятные состояния в дискретные моменты времени называется дискретным источником (ДИ). Характеристикой ДИ является отсутствие или наличие внутренней памяти. Рассмотрим эти два типа ДИ.

Дискретный источник называется источником Бернулли, если очередное сообщение (символ или последовательность) не зависит от всех предыдущих, иными словами все сообщения независимы и характеризуются только своими вероятностями. Примером процессов, порождаемых источником Бернулли являются, например, результаты бросания монеты или игрального кубика. Результаты бросания кубика - сигнал с равными вероятностями всех событий. Источник такого сигнала называют еще комбинаторным. Если же на кубик нанести числа 1, 2, 2, 3, 3, 3, то мы получим прекрасный источник разновероятных сообщений Бернулли. Если в ансамбле сообщений соблюдается одно из двух правил:

p(x_i) ³ p(x_j) для любого i > j или

p(x_i) £ p(x_j) для любого i < j,

то такой источник называется монотонным.

Дискретный источник Бернулли не обладает внутренней памятью.

Источник Маркова - более сложная модель. В ней предполагается, что вероятность появления очередного сигнала зависит от n предыдущих сигналов. Соответственно получается источник сигнала Маркова n-го порядка. Чем больше n, тем сложнее учет и оценка зависимостей, поэтому на практике ограничиваются значением n=1..2. Очевидно, что модель Бернулли-это модель Маркова при n=0.

Если для источника Бернулли необходимо знать только вероятности отдельных сообщений, то для источника Маркова необходимо получить условные вероятности в виде n+1-мерных матриц. Для Марковского источника первого порядка это будет двумерная матрица размера LxL, где каждый i-й столбец показывает вероятность перехода от сообщения x_i к сообщению x_j, например:

Таблица 1.

	x1	...	xi-1	xi	xi+1	...	xL
x1	p1,1	...	...	p1,i	...	...	p1,L
...	...	...	...	...	...	...	...
xj-1	pj-1,1	...	...	pj-1,i	...	...	pj-1,L
xj	pj,1	...	...	pj,i	...	...	pj,L
xj+1	pj+1,1	...	...	pj+1,i	...	...	pj+1,L
...	...	...	...	...	...	...	...
xL	pL,1	...	...	pL,i	...	...	pL,L

 

(Сумма вероятностей любой строки или столбца должна равняться единице.)

Примером источника Маркова являются буквы русского (или, например, английского алфавита), поскольку появление в слове очередной буквы очень сильно зависит от предыдущих букв или даже слов.

Дискретный источник Маркова является источником с внутренней памятью. При дальнейшем обсуждении материалов данной части курса в качестве дискретного источника Маркова будет рассматриваться процесс с дискретным состоянием (возможные состояния процесса x_{i ,} x_i+1… можно заранее определить и переход в состояние x_{j ,} x_j+1 … происходит скачком) и непрерывным временем (моменты возможных переходов из состояния в состояние случайны). Для обсуждения материалов темы следует установить, что при каждом переходе от x_i к х _j создается один символ.

Энтропия дискретного источника независимых сообщений.

Рассмотрим ДИ с конечным числом состояний. Для каждого возможного состояния i имеется некоторое множество вероятностей p_i(j) создания различных возможных символов j. Следовательно, для каждого состояния i существует энтропия H_i. Энтропия источника определяется как среднее значение величин H_i, которые осреднены в соответствии с вероятностями осуществления соответствующих событий

[1]

Выражение [1] определяет энтропию на символ текста. Если Марковский процесс развивается с определенной скоростью, можно говорить об энтропии в секунду

,

где f_i – средняя частота (появлений в секунду) состояния i.

Если m – среднее число символов, создаваемых за одну секунду, то

H` = mH.

Величины Н или Н` измеряют количество информации, создаваемое источником, на символ или в секунду. При основании логарифмов 2 – количество битов (бит) на символ или в секунду.

Если символы в последовательности независимы,

где p_i – вероятность символа i.

Рассмотрим длинное сообщение, состоящее из N символов. Оно будет с большой вероятностью содержать p_iN раз первый символ, p_i+1N раз второй символ и т. д. Тогда вероятность данного конкретного сообщения будет приближенно равна

p =p_i ^piN p_i+1 ^pi+1N …p_n ^pnN .

Прологарифмировав, получим

или log p = - NH.

Окончательно [2]

Таким образом, энтропия Н длинной последовательности приближенно равна логарифму обратной величины вероятности типичной длинной последовательности, поделенному на число символов в последовательности. Этот вывод верен для любого источника.

ТЕОРЕМА 3. Для любых заданных ε>0 и δ>0 можно найти такое N₀ , что последовательности любой длины N ≥ N₀ распадаются на два класса:

1. множество последовательностей, суммарная вероятность которых меньше, чем ε;

2. остаток, все члены которого обладают вероятностями, удовлетворяющими неравенству

Последнее выражение можно трактовать следующим образом: почти достоверно, что отношениевесьма близко к Н, когда N велико.

Доказательство.

Предположив источник эргодическим, можем применить закон больших чисел к заданной последовательности. Подобное допущение позволяет утверждать, что число непосредственных переходов из состояния i в состояние j в последовательности большой длины N приблизительно пропорционально вероятности нахождения в состоянии i , (обозначим как P_i), умноженной на вероятность перехода p_i,j, т. е. определяется произведением P_i p _i,jN. Если N достаточно велико, то вероятность ошибки, не превосходящей δ, будет в этом случае меньше, чем έ, так что все числа, кроме множества малой вероятности, заключены в пределах (P_i p _i,j ±δ)N (для удобства написания обозначим данное произведение буквой v)

Следовательно, все последовательности, за исключением сколь угодно малой доли, имеют вероятность p:

p = Πp_ij^v

и имеет место соотношение

илиЧто и требовалось доказать.

Рассмотрим ряд последовательностей длины N, имеющих определенные суммарные вероятности. Расположим их в ряд в порядке уменьшения вероятностей. Введем величину n(q) – число последовательностей, которые необходимо взять из ряда, начиная с наиболее вероятной последовательности, для того чтобы для взятых последовательностей накопилась суммарная вероятность q.

ТЕОРЕМА 4. Когда q не равно нулю или единице,

[3]

Mожно интерпретировать величину log n(q) как число бит, требуемых для задания последовательности, когда рассматриваются только наиболее вероятные последовательности с суммарной вероятностью q. Тогда

есть число бит на символ, необходимых для задания последовательностей. Теорема свидетельствует, что для больших N это число не зависит от q и равно H. Быстрота возрастания логарифма числа сравнительно вероятных последовательностей определяется величиной H независимо от толкования смысла слов “сравнительно вероятный”. Выводы показывают, что в большинстве случаев длинные последовательности можно рассматривать так, как если бы их было 2^HN, и каждая имела вероятность 2 ^-HN. Величины H и H^’ могут быть найдены с помощью предельных операций непосредственно из статистической структуры последовательности сообщений без привлечения вероятностей состояний и переходных вероятностей.

ТЕОРЕМА 5. Пусть p(B_i) – вероятность того, что источник создает последовательность символов B_i. Пусть

G_N = - 1/N p(B_i) log (B_i),

где суммирование распространяется на все последовательности B, содержащие N символов. Тогда G – монотонно убывающая функция от N и

lim G_N = H при N

ТЕОРЕМА 6. Пусть p(B_i, S_j) – вероятность того, что появится последовательность B_i и после нее появится символ S_j, а

p_Bi (S_j) = p(Bi, S_j)/ p (B_i)

условная вероятность того, что после B_i появится S_j. Пусть

где суммирование проводится по всем возможным последовательностям B_i из (N – 1) символов и по всем символам S_j. Тогда F_N – монотонно убывающая функция от N

F_N = NG_N – (N – 1)G_{N - 1}

F_N G_N и, следовательно,

lim F_N = H.

N→∞

Доказательство.

Если вероятность перехода из состояния с N – 1 буквой в состояние с N буквами определяется выражением p _Bi (S _j) = p(B _i, S _j) / p(B _i), то , подставив его в выражение для F_N, получим

С учетом свойства N – грамм второе слагаемое можно представить в виде

Таким образом, F_N = NH_N – (N-1)H_{N --1}

Далее выпишем все последовательности В_i , начиная с первой

F₁ = H₁

F₂ =2H₂ – H₁

F₃ = 3H₃ – 2H₂

…

F_N = NH_N – (N – 1)H_N--1

Просуммировав равенства, получим

Так как F_N ≤ F_N-1, то F_N ≤ H_N ≤ H . Последнее означает, что с учетом вероятностей переходов Марковская модель источника дает лучшее приближение к истинной энтропии H, чем модель источника на основе N – грамм.

Что и требовалось доказать.

Отметим, что рассмотренные теоремы показывают, какой ряд приближений к H может быть получен с помощью рассмотрения только статистической структуры последовательностей, охватывающей 1, 2, …, N символов. F_N является лучшим приближением. Фактически F_N является энтропией N – го приближения к источнику рассмотренного нами типа. Если нет никаких статистических связей, распространяющихся более чем на N символов, т.е., если условная вероятность появления следующего символа при условии, что значения предшествовавших (N – 1) символов известны, не изменяется от добавления сведений о любых ранее стоящих символах, то тогда F_N = H F. является условной энтропией следующего символа, когда известны (N – 1) предыдущих. В то же время G_N – есть энтропия на символ последовательности из N символов.

Отношение энтропии источника к максимальному значению, которого могла бы достичь энтропия при тех же символах, назовем относительной энтропией источника.

Относительная энтропия является МАКСИМАЛЬНЫМ СЖАТИЕМ, которое можно осуществить кодированием при помощи того же самого алфавита.

Единица минус относительная энтропия есть ИЗБЫТОЧНОСТЬ. Исследованиями показано, что избыточность английского текста, если не рассматривать статистическую структуру, относящуюся более чем к восьми буквам, составляет примерно 50 %. Это значит, когда англичане пишут текст, половина знаков текста определяется структурой языка, и только половина выбирается свободно.

Представление операций кодирования и декодирования.

Мы рассмотрели энтропию источника для случаев длинных последовательностей, установив, что логарифм обратной величины вероятности, поделенный на число символов последовательности, сколь угодно близок к величине энтропии источника. Реальный источник накладывает ограничения, выражающиеся в том, что последовательности ограничены по длине. Представим математические операции, выполняемые передатчиком телекоммуникационной системы при кодировании. Назовем передатчик дискретным преобразователем. На вход преобразователя поступает последовательность входных символов, а на выходе получается последовательность выходных символов. Поскольку преобразователь может обладать внутренней памятью, отметим, что выходной символ зависит не только от данного входного символа, но и от всех предыдущих. Предположим, что внутренняя память конечна, т. е. существует конечное число m возможных состояний преобразователя и при этом очередной выходной символ является функцией от соответствующего входного символа и от состояния, в котором находится преобразователь. Следующее состояние преобразователя будет другой функцией от этих же аргументов. Таким образом, преобразователь может быть описан двумя функциями:

y = f(x_n, a_n)

a_n+1 = g(x_n, a_n),

где x_n – n-й входной символ,

a_n – cсостояние преобразователя к моменту ввода n-го входного символа,

y_n – выходной символ (или группа выходных символов), создаваемый, когда на вход поступает x и преобразователь находится в состоянии a_n.

Если выходные символы одного преобразователя могут служить входными символами для другого, то преобразователи могут быть соединены последовательно. В результате также получится некоторый преобразователь. Если существует второй преобразователь, который при соединении его входа с выходом первого восстанавливает исходный сигнал, то первый преобразователь называется невырожденным, а второй - обратным к первому.

ТЕОРЕМА 7. Выход преобразователя с конечным числом состояний, подключенный к статистическому источнику с конечным числом состояний, представляет собой статистический источник с конечным числом состояний, причем энтропия этого источника (в единицу времени) меньше или равна энтропии источника на входе. Если преобразователь невырожденный, то энтропии равны.

Пусть ά представляет собой состояние источника, который создает последовательность символов x, и пусть β – состояние преобразователя, который создает на выходе блоки символов y. Система, полученная в результате соединения источника с преобразователем, может быть представлена с помощью произведения “пространств состояний”, состоящего из пар (ά, β). Переход из точки (ά₁, β₁) этого пространства в точку (ά₂,β₂) соответствует созданию источником такого символа x, который изменит состояние преобразователя β₁ на β₂. При этом преобразователем создается блок символов y_i. Энтропия источника на выходе может быть вычислена как взвешенная сумма по всем состояниям. Если мы просуммируем сначала по β, то каждый получающийся в результате член будет не больше соответствующего члена для ά и, следовательно, энтропия не увеличивается. Для преобразователя на передающей стороне H₁ = H_2..

ТЕОРЕМА 8. Пусть система ограничений, рассматриваемая как канал, имеет пропускную способность C = logW. Если положить

где - длительность s – го символа, ведущего от состояния i к состоянию j, а B_i удовлетворяет условию

то энтропия Н максимальна и равна С.

Доказательство.

Допустим, что в канал поступают последовательности символов, на которые наложен ряд ограничений, задающих систему с конечным числом состояний, описываемую Марковским процессом. Пусть l_i,j^(s) есть длительности различных символов, которые могут появиться при переходе из состояния х_i в состояние x_j (см. табл.1).Каково распределение вероятностей для различных состояний P_i и вероятностей р_i,j^(s) выбора символов s при переходе из состояния x_i в состояние х _j., для которого максимизируется скорость создания информации при данных ограничениях? Эти ограничения определяют дискретный канал, а максимальная скорость должна быть меньше или равна пропускной способности С этого канала. Действительно, если все группы большой длительности были бы равновероятны, то в результате получилась бы именно эта скорость, и, если это возможно, такая скорость была бы наилучшей. Покажем, что эта скорость может быть достигнута при надлежащем выборе P_i и Р _ij^s

Рассматриваемая скорость равна

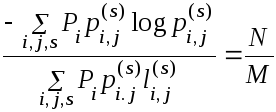
Пусть по предположению

где В_i удовлетворяет системе уравнений

Эта однородная система имеет ненулевое решение, так как W обращает в нуль детерминант из коэффициентов

Определенные таким образом вероятности p_i,j^(s) могут служить переходными вероятностями, так как сумма вероятностей выхода из любой фиксированной узловой точки равна 1, что подтверждается следующими преобразованиями

Эти вероятности неотрицательны. Подставляя значения p_i,j^(s) в общее выражение для скорости, получим

Следовательно, скорость, достигаемая для этого набора вероятностей перехода, равна С, и так как эта скорость не может быть превышена, то она максимальна.

Основная теорема для канала без шума.

Выше мы определили величину Н как скорость создания информации источником. Подтвердим это определение доказательством того, что энтропия источника определяет пропускную способность канала, необходимую при наиболее эффективном кодировании.

ТЕОРЕМА 9. Пусть источник имеет энтропию Н (бит на символ), а канал имеет пропускную способность С (бит в секунду). Тогда можно закодировать сообщения на выходе источника таким образом, чтобы передавать символы по каналу со средней скоростью С / Н – ε символов в одну секунду, где ε – сколь угодно мало. Передавать со средней скоростью, большей, чем С/Н, невозможно.

Доказательство.

Заменим выражение r = (С/H – ε) симв./с на выражение R = rH = C – ξ бит/ с, а выражение r > C/H симв./с на выражение R = rH > C бит/с. Тогда R = rH бит/с – производительность источника, чтд.

Рассмотрим множество всех последовательностей из N символов, создаваемых источником. Применим для доказательства теорему об ε – энтропии. При большом N все последовательности можно разделить на две группы: одна из групп содержит меньше 2^(H+η)N членов; другая содержит меньше чем 2^RN членов (где R – логарифм числа различных символов) и имеет суммарную вероятность, меньшую μ. С ростом N величины η и μ стремятся к нулю. Число сигналов в канале, имеющих длительность Т, больше 2^(С-θ)Т , где θ мало, когда Т велико. Выберем длительность сигнала из условия

Тогда найдется достаточное число последовательностей символов в канале для высоко вероятностной группы, когда N и T достаточно велики (сколь бы малым ни было выбрано λ), и несколько добавочных последовательностей. Высоковероятная группа произвольным, взаимнооднозначным образом кодируется в это множество последовательностей символов канала. Остающиеся последовательности источника кодируются в более длинные последовательности канала, начинающиеся и заканчивающиеся одной из добавочных последовательностей, не использованных для высоковероятной группы, причем эта последовательность действует как начальный и конечный сигналы, указывающие на использование в промежутке иного кода. Между этими сигналами оставляют временной интервал, достаточный для того, чтобы для этого временного интервала в канале существовало достаточно различных последовательностей для всех маловероятных сообщений. Условие для выбора данного интервала запишем следующим образом

φ – сколь угодно малая величина.

Тогда среднее время передачи символов сообщения в секунду Т‘ должно быть не меньше суммы

Т` = Т + Т_i

В соответствии с теоремой об ε – энтропии имеем

Подставив значения Т и Т_i , получим

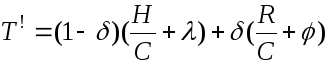
При увеличении N величины δ , λ и φ стремятся к нулю и скорость передачи символов сообщения в секунду 1/Т` стремится к величине отношения С/Н.