Описания лабораторных работ

Механика деформации твердого тела

Тема: ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА

Введение

Деформация тел- изменение их размеров и формы - происходит под действием сил, приложенных к данным телам.

Деформация называется упругой, если она исчезает после прекращения действия силы, ипластической, если она сохраняется и после снятия нагрузки.

Величина, равная отношению силы к площади поверхности, на которую сила действует, называется напряжением или усилием. Благодаря взаимодействию частей тела друг с другом напряжение передается во все точки тела, т.е. весь его объем оказывается в напряженном состоянии. Если силаF_nнаправлена по нормали (т.е. перпендикулярно) к поверхности, то напряжение называетсянормальными обозначается буквойσ:

(1)

Если сила F_tнаправлена по касательной к поверхности, то напряжение называетсятангенциальными обозначается буквойτ:

(2)

Все возможные виды упругих деформаций твердого тела могут быть сведены к двум основным: растяжение (или сжатие), возникающие при нормальных напряжениях, и сдвиг под действием касательных напряжений.

Деформация растяжения. Деформация растяжения возникает под действием силF_n, направленных по нормали к той поверхности, к которой они приложены.

Если к концам однородного стержня постоянного сечения приложить направленные вдоль его оси силы F₁ иF₂(F₁ =F₂ =F_n), действие которых равномерно распределено по всему сечению, то длина стержняLполучит положительное (при растяжении) или отрицательное (при сжатии) приращение ΔL (рис. 1). При этом каждый произвольно выбранный элемент стержняl получает приращение Δl, пропорциональное его длине, так что для всех элементов стержня отношение Δl / l оказывается одинаковым. Следовательно, в качестве величины, характеризующей деформацию стержня, можно взять егоотносительное удлинение:

	(3)
Рис. 1

Из (3) видно, что ε - безразмерная величина. В случае растяжения ε > 0, в случае сжатия ε < 0. Из опыта известно, что относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:

,

(4)

где α называетсякоэффициентом упругостии зависит только от свойств материала стержня.

Воспользовавшись данным выше определением нормального напряжения (1), выражение (4) можно записать:

(5)

т. е. относительное удлинение пропорционально нормальному напряжению.

Для характеристики упругих свойств материала наряду с коэффициентом упругости αпользуются обратной ему величиной, которая называетсямодулем Юнга:

(6)

Таким образом, выражение (5) принимает вид

(7)

Отсюда следует, что модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение ε было бы равно единице (т.е. приращение длины ΔL, было бы равно первоначальной длине).

С учетом (1) и (3) соотношение (7) может быть приведено к следующему виду:

(8)

где k - постоянный для данного стержня коэффициент.

Согласно выражению (8) удлинение стержня при упругой деформации пропорционально действующей на стержень силе. Это соотношение выражает закон Гука для данной деформации. Этот закон выполняется только до тех пор, пока не достигается предел упругости.

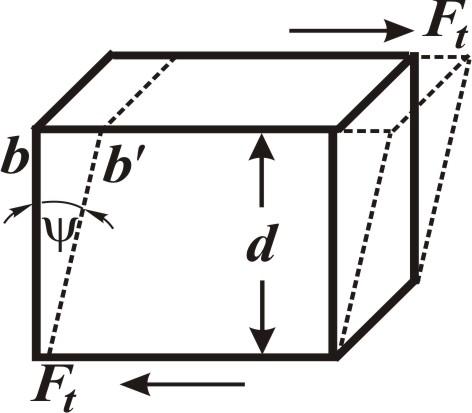
Деформация сдвига.Деформация сдвига возникает под влиянием силF_t, касательных к той поверхности, на которую они действуют. Под влиянием этих сил происходит параллельный сдвиг одного слоя тела относительно другого. Любая прямая, проходящая вначале перпендикулярно к слоям, после их сдвига окажется повернутой на некоторый угол ψ (рис. 2).

		При малом значении угла ψ приближенно имеем , (9) где d - толщина тела,bb' -абсолютная величина сдвига верхнего слоя относительно нижнего. Угол сдвига ψ характеризует относительный сдвиг слоев, и в пределах применимости закона Гука можно написать
	Рис. 2
			(10)

Используя определение тангенциального напряжения (2), получаем:

(11)

т.е. угол сдвига будет прямо пропорционален приложенному к телу усилию. Постоянная величина n, зависящая от материала тела, называетсякоэффициентом сдвига. ВеличинаG, обратная коэффициенту сдвига, называетсямодулем сдвига

(12)

Если угол ψ равен одному радиану, то G = τ , т.е. в пределах упругости модуль сдвига численно равен касательному усилию, вызывающему угол сдвига, равный одному радиану.

Деформация сдвига имеет место, например, при закручивании однородного круглого стержня. Если один конец круглого стержня закрепить неподвижно, а к другому приложить вращательный момент, то одно основание стержня повернется вокруг оси стержня на некоторый угол относительно другого основания. Легко видеть, что деформация при кручении представляет собой деформацию сдвига. Действительно, если разбить стержень на элементарные коаксиальные слои, то закручивание приведет к сдвигу каждого из таких слоев по отношению к соседним с ним слоям.

Можно показать [2], произведя расчет, что угол закручивания цилиндрического стержня будет определяться следующим выражением:

(13)

где L - длина стержня,r - радиус стержня,M - момент силы, действующей на стержень,G - модуль сдвига. Обозначив величину

(14)

имеем

(15)

Это соотношение выражает закон Гука при кручении. Величину χ называют модулем кручения, в отличие от модуля сдвига. Она характеризует конкретный стержень и зависит от его размеров [1].

Лабораторная работа № 5

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО РАСТЯЖЕНИЮ ПРОВОЛОКИ.

Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: "Деформация твердого тела."

Постановка экспериментальной задачи. Преобразуя уравнение (8), можно получить выражение для определения модуля Юнга

(5.1)

Таким образом, для нахождения модуля Юнга надо определить удлинение проволоки ∆Lпод действием приложенной к ней силыF при известных длине проволокиL и площади поперечного сечения.

Описание экспериментальной установки. Установка (рис. 5.1)

Рис. 5.1	Рис 5.2

состоит из проволоки, закрепленной в кронштейне А, к нижнему концу которой на оправеВподвешивается грузР, вес которого играет роль деформирующей силы. ОправаВсоединена с горизонтальным рычагомС, который фиксирует вертикальное положение проволоки и делает невозможными маятникообразные раскачивания оправы. РычагСфиксируется винтомVдля предохранения проволоки от толчков при снимании и подвешивании гирь. ГрузQнебольшого веса служит для распрямления проволоки. Для определения удлинения проволоки под действием груза служит зеркальцеON, прикрепленное вертикально к горизонтальному рычагуОВ, опирающемуся на поверхность оправыВ, а также вертикальная шкалаFи осветительD.

Пусть под действием силы веса груза РрычагОВповернулся на уголВОВ' = α (рис. 5.2). Тогда и зеркальцеONотклонится на равный ему уголNОN'. При этом луч, вышедший из точкиD, отразившись от зеркалаОN', попадет в точкуFна шкале. Так как плоскости зеркальца и рычага взаимно перпендикулярны, то лучОЕ, проведенный через точкуВ', является нормалью к поверхностиОN'и условие равенства углов падения и отражения будет иметь вид:

DOE = EOF = α.

(5.2)

Восстановив из точки В' перпендикуляр, получим отрезокВ'К, длина которого равна вертикальной составляющей смещения рычагаОВ. Из треугольникаКОВ'следует:

В'К = r sinα,

(5.3)

где r– длина рычагаОВ или ОВ'.

Если обозначить расстояние от зеркальца до шкалы R, то из треугольникаDOFс учетом (5.2) имеем:

х/R = tg2α,

(5.4)

где x- отсчет на шкале, являющийся координатой точкиF. Воспользуемся малостью угла α:

tg2α = 2 tgα = 2 sinα

(5.5)

Теперь выражение (5.3) можно записать:

В'К = r х/2R

(5.6)

Кроме растяжения проволоки груз Рпроизводит прогиб кронштейнаА.Поэтому длина отрезкаВ'Кскладывается из удлинения проволоки∆Lи прогиба кронштейна АА'(на рисунке не обозначено).

Чтобы определить величину прогиба кронштейна, груз следует подвесить на крючок, соединенный посредством двух шнуров с перекладинами кронштейна, и получить отсчет x₀на шкале, являющийся координатой точкиF₀, в которую в этом случае попадет отраженный от зеркальца луч.

Величина АА'рассчитывается аналогично величинеВ'К:

АА' = r х0/2R

(5.7)

Используя выражения (5.6) и (5.7) получаем, что удлинение проволоки равно:

∆L = В'К - АА' = r(х - х0)/2R

(5.8)

Подставляя в (5.1) значение ∆L,а также площадь поперечного сечения проволоки, находим величину модуля Юнга:

,

(5.9)

где d– диаметр проволоки.

Порядок выполнения работы.

1. Произвести при помощи миллиметровой линейки однократное измерение длины проволоки L и расстояния от шкалы до зеркальцаR,а также пять раз измерить диаметр проволокиd при помощи микрометра. ДлинаrрычагаОВуказана на установке.

2. Взять грузы 0.5, 1.0, 1.5, 2.0, 2.5 кг и снять для них отсчеты x₀ иx, для чего каждый груз следует подвешивать дважды: на крючок, соединенный с перекладинами кронштейна и на крючок проволоки.

Формулы для расчета результата эксперимента и его погрешности.

Как видно из формулы (5.9), зависимость Р = f(х – х₀)является линейной. Следовательно, модуль Юнга следует рассчитывать по формуле:

,

(5.10)

где а– угловой коэффициент прямойР = f(х – х₀), который находят по методу наименьших квадратов.

Доверительные границы модуля Юнга при этом равны:

(5.11)

Погрешности измерения LиR,обозначенные соответственно∆lи∆R,определяются ценой деления линейки,∆d следует вычислить по алгоритму прямых измерений,∆r= 0.1 мм,∆арассчитывается по методу наименьших квадратов.

Содержание отчета.

1. Значения измеренных величин L, dиR,и их погрешностей.

2. Расчет значения углового коэффициента аи его доверительных границ по методу наименьших квадратов по пяти измеренным значениям.

3. Расчет значения модуля Юнга по формуле (5.10) и его доверительных границ по формуле (5.11) в системе СИ.

4. График зависимости Р = f(х – х₀)и угловой коэффициент этой прямой, определенный из графика.

Контрольные вопросы

1. Какие бывают виды деформаций?

2. Каков физический смысл модуля Юнга?

3. Как формулируется закон Гука и при каких условиях он справедлив?

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ПО КРУЧЕНИЮ

Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: "Деформация твердого тела"

Постановка экспериментальной задачи.Модуль сдвига можно определить, исследуя деформацию закручивания однородного круглого стержня. Если к круглому стержню радиусаrи длинойLприложить вращающий моментМ, то угол закручивания φ определится соотношением

,

(6.1)

где G - модуль сдвига материала, из которого сделан стержень.

Описание экспериментальной установки.В данной работе для определения модуля сдвига используется установка, схематически изображенная на рис. 6.1

Рис. 6.1	Рис 6.2

Верхний конец вертикального стержня С жестко закреплен на стойке, а нижний соединен с диском Д. Момент M, закручивающий стержень, создают две скрепленные с ободом диска нити, перекинутые через блоки Б. К концам нитей подвешиваются одинаковые грузы P₁ и P₂ Конец стержня снабжен зеркальцем 3. Для определения угла закручивания надо луч осветителя направить на зеркальце и отраженный от него зайчик установить на нулевое деление шкалы, расположенной на расстоянии D от зеркальца. Из рис. 6.2 видно, что при повороте зеркальца на угол φ нормаль ON к новому положению зеркальца составит с прежним ееположением OC угол NOC = φ. Отраженный от зеркальца луч повернется на угол, равный 2φ. Как следует из рис. 6.2, , гдеD – расстояние от зеркала до шкалы, а d -смещение зайчика по шкале. Отсюда угол поворота стержня в радианах определяется из формулы

(6.2)

При вычислении угла φ по этой формуле членами разложения в ряд со степенями больше 2 можно пренебречь, ввиду их малости, тогда

.

(6.3)

Момент силы, действующий на стержень, равен M =PR, где P – суммарный вес грузов P₁ и P₂ , R – радиус диска Д (плечо вращающей силы). Тогда формула (13) примет вид

.

(6.4)

В линейной зависимости φ = f(P)тангенс угла наклонаtgθ прямой к оси абсцисс будет равен

.

(6.5)

Отсюда модуль сдвига материала стержня будет определяться через tgθ

.

(6.6)

Порядок выполнения работы

Устанавливают осветитель так, чтобы отраженный от зеркальца луч фокусировался на нулевом делении шкалы, шкала должна быть перпендикулярна лучу. На грузодержатели, левый и правый, кладут по одному грузу и определяют отклонение зайчика по шкале d₁. Затем увеличивают нагрузку; кладут последовательно по 2, 3 и т.д. до 8 грузов на каждый грузодержатель, каждый раз определяя отклонениеd_n.

Но формуле (6.3) вычисляют значения углов поворота φ стержня для каждой суммарной нагрузки и строят график зависимости φ (угла поворота стержня в радианах) от Р(значения нагрузки вtgθ ньютонах).

Эту линейную зависимость обрабатывают по методу наименьших квадратов, определяют тангенс угла наклона прямой tgθ и его доверительные границы Δtgθ. Затем по формуле (6.6) определяют величину модуля сдвигаGматериала стержня.

Формулы для расчета погрешности результата эксперимента Погрешность определяют по следующей формуле:

.

(6.7)

Параметры установки:

Стальной стержень	Латунный стержень
L = (128,7± 0,1) см R = (50,0± 0,1) мм 2r = (6,00± 0,01) мм	L = (128,8± 0,1) см R = (49,5± 0,1) мм 2r = (4,95± 0,01) мм

Содержание отчета.

1. Общий вес грузов на грузодержателях выраженный в ньютонах (Н), отсчет по шкале осветителяd и расстояниеDот зеркальца на установке до шкалы в миллиметрах.

2. Расчет величины углов поворота стержня для всех нагрузок.

3. График зависимости угла поворота стержня в радианах от величины груза в ньютонах. Эта зависимость должна быть линейной. По графику необходимо определить приблизительное значение тангенса угла наклона этой прямой к оси абсцисс – tgθ.

4. Расчет по методу наименьших квадратов tgθ.

5. Расчет величины Gпо формуле (6.6).

6. Расчет погрешности модуля сдвига по формуле (6.7).

7. Окончательный результат модуля сдвига с погрешностью в системе СИ.

Контрольные вопросы

• Чем отличается деформация кручения от деформации растяжения?

• В каких случаях зависимость φ =f(P)будет линейной?

• Что дает использование зеркальца в данной работе?

• Что такое модуль кручения? Как он связан с модулем сдвига?

Лабораторная работа 7

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА КРУГЛОГО СТЕРЖНЯ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: “Деформация твердого тела”

Физическое обоснование эксперимента

Моментом силы относительно некоторой точки О называется векторная величинаМ, определяемая выражением:,где – радиус-вектор, проведенный из точки О в точку приложения силы

Моментом инерции системы материальных точек относительно осиСназывается физическая величина равная сумме произведений их масс на квадраты расстояний до оси: I  = m_ir_i²

К твердому телу, совершающему вращательные движения, может быть применен закон вращательного движения

,

(7.1)

где М– момент возвращающей силы относительно оси вращения,I– момент инерции тела относительно той же оси,  – угловое ускорение.

Если закрепить верхний конец круглого стержня, а нижний конец с прикрепленным к нему диском повернуть на угол φ и отпустить, то стержень может совершать крутильные колебания, при этом роль момента возвращающей силы будет выполнять момент силы упругости деформированного стержня.

Из уравнения (15) и третьего закона Ньютона видно, что момент силы равен

.

(7.2)

Подставляя это значение в (7.1), получим дифференциальное уравнение, описывающее движение колеблющегося стержня

.

(7.3)

Как известно из теории дифференциальных уравнений, решением этого уравнения является функция вида φ = φ_оcos(ωt+ α), где- круговая частота.

Период таких колебаний равен соответственно:

.

(7.4)

Отсюда можно найти выражение для модуля сдвига G, если в (7.4) подставить значение величины χ из (14):.

Окончательно имеем

.

(7.5)

Таким образом, для определения модуля сдвига Gметодом крутильных колебаний необходимо определить длину стержня L, его радиусr, момент инерции колеблющегося телаIи период его колебанийT.

Для расчета момента инерции рассматриваемого маятника используется дополнительное массивное кольцо K, момент инерции которогоI_o можно вычислить из геометрических размеров:

,

(7.6)

где R₁ и R₂– внутренний и внешний радиусы кольца,m– его масса.

Если положить такое кольцо концентрически на диск (рис.7.1), то момент инерции получившейся системы будет равен (I + I_o), т. к. момент инерции величина аддитивная. Период крутильных колебанийТ₁ этой системы в соответствии с формулой (7.4) будет:

.

(7.7)

Из выражений (7.7) и (7.4) получаем

.

(7.8)

Таким образом, определив момент инерции крутильного маятника, можно по формуле (7.5) можно определить модуль сдвига G.

Метод исследования и описание установки

Рис. 7.1

К нижнему концу зажатой вверху толстой проволоки, играющей роль круглого стержня, прикреплен горизонтальный диск (рис. 7.1). На этот диск может накладываться дополнительно массивное кольцо К. На диске Д нанесена стрелка, которая при положении равновесия должна находиться против неподвижной метки на стене.

Порядок выполнения работы и обработка результатов измерений

1. Повернуть диск на некоторый угол, отпустить его. Вследствие этого диск начинает совершать крутильные колебания. При помощи секундомера определить время нескольких, например, 30 ÷ 50, прохождений черты на диске через положение равновесия. Счет прохождений надо начинать с нуля. Деля это время на число прохождений в одну сторону, получают период колебаний Т. Измерения проделать 5 раз.

2. Опустить на диск концентрически металлическое кольцо и определить период колебаний Т₁ с кольцом так же, как определилиТ.

3. Измерить с помощью линейки длину стержня Lи его внутренний и внешний радиусы -R₁иR₂ .

4. Измерить с помощью микрометра диаметр стержня 5 раз. Найти среднее значение радиуса r.

5. По формуле (7.5) рассчитать значение модуля сдвига. Расчеты следует проводить в системе СИ.

Формула для расчета погрешности результата эксперимента

Из результатов 5-ти измерений TиT₁ по алгоритму прямых измерений определить средние значенияTиT₁и их доверительные границы∆Ти∆Т₁. Аналогично определяют доверительные границы∆r. Погрешности ΔL,∆R₁,∆R₂ определяются ценой деления измерительной линейки.

Доверительные границы для модуля сдвига можно вычислить по следующей формуле (учитывая, что ∆R₁=∆R₂=∆R):

.

Содержание отчёта

1. Таблицы экспериментально полученных значений периода колебаний ТиТ₁, расчет их средних значений и их доверительных границ.

2. Величины R₁,R₂,L,r,mи их погрешности.

3. Расчёт момента инерции кольца I_o и момента инерции всей системыI.

4. Рассчитанное значение величины модуля сдвига Gи ее доверительные границы∆Gв системе СИ.

Контрольные вопросы

• В чем заключается метод крутильных колебаний для определения модуля сдвига?

• От каких величин зависит период крутильных колебаний диска в данной установке?

• Погрешность, каких измеряемых величин, вносит наибольший вклад в погрешность окончательного результата?

• Для чего необходимо кольцо?

Приложение