Физика методички / Механика / Лабораторная работа №4

Введение

Ускорение свободного падения

Любое тело испытывает силу, обусловленную притяжением Земли – F =, здесь G – гравитационная постоянная, M – масса Земли, m – масса тела, R – расстояние от центра Земли до тела. В случае, когда тело на поверхности Земли или недалеко от нее (по сравнению с радиусом Земли) - R равно радиусу Земли.

Для описания гравитационного взаимодействия вводится понятие - гравитационное поле. Напряженностью гравитационного поля называют величину численно равную силе действующей на единичную массу .

В случае если мы рассматриваем гравитационное поле Земли, то эту величину называют ускорением свободного падения - g. Поле можно рассматривать как математическую функцию координат и времени. Гравитационное поле можно определить в любой точке пространства.

из эксперимента известно, что ускорение свободного падения величина постоянная, что все тела падают с одинаковым ускорением. Это правильно, если проводить опыты в одном месте. Другими словами ускорение g не зависит от массы тела. Но оказывается, оно зависит от места, где проводится эксперимент.

Эта зависимость обусловлена несколькими причинами:

0. Земля - неинерциальная система отсчета, следовательно, на все, находящиеся на ней тела, действует центробежная сила, при чем эта сила зависит от широты. Нет ее только на полюсе, а на экваторе она максимальна.

1. Земля сплюснута с полюсов. Тело, находящееся на полюсе ближе к центру Земли, чем на экваторе.

2. Поверхность Земли неровная, и ускорение зависит от высоты места. А что принять за поверхность земли? Принято за поверхность земли считать поверхность, совпадающую со свободной невозмущенной поверхностью воды земных океанов.

Выясним влияние силы инерции.

Наблюдаемое ускорение обусловлено равнодействующей двух сил: силы притяжения и силы инерции (центробежной силы инерции).

F_т = f_пр + f_in = mg

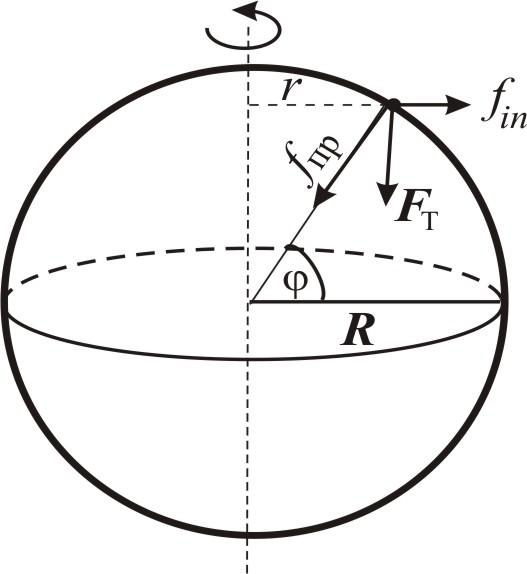f _in << f_пр, так что отличие F_т от f_пр невелико, на рисунке масштаб сильно искажен.

Как известно, центробежная сила равна:

f_in = mω² r =mω²Rcos,

где r  –расстояние от тела до оси вращения, ω – угловая скорость, R – радиус Земли, φ – широта.

Нетрудно рассчитать, что, например, на экваторе поправка к g, обусловленная центробежной силой будет равна 0,0338 м/с².

Такую фигуру, как имеет Земля, принято называть геоидом. Геоид по форме очень близок к эллипсоиду вращения.

Представляя Землю в виде такого эллипсоида и учтя центробежную силу, французский математик Клеро вывел вид формулы, выражающей зависимость ускорения силы тяжести от широты (теорема Клеро):

g_=g_о(1+ 0.00529sin²)

здесь g_о значение ускорения силы тяжести на экваторе, равное 9.7803 м/сек², g_ - ускорение на широте .

Лабораторная работа 4

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА

Задачи работы

1. Определение ускорения свободного падения.

2. Определение моментов инерции маятника относительно разных осей.

Физическое обоснование эксперимента

Вращение твердого тела

Моментом силы относительно некоторой точки О называется векторная величины М, определяемая выражением:

, где – радиус-вектор, проведенный из точки О в точку приложения силы. Модуль момента силы равен:

M = f∙r∙sinα, где α – угол между направлением силы и радиус-вектора, r∙sinα называется плечом силы

Моментом инерции системы материальных точек относительно оси С называется физическая величина равная сумме произведений их масс на квадраты расстояний до оси I  = m_ir_i².

Вращение твердого тела подчиняется закону:

,

(4.1)

где - угловое ускорение. Легко видеть, что это уравнение можно рассматривать как аналог 2-го закона Ньютона, где сила заменена моментом силы, масса - моментом инерции, ускорение - угловым ускорением.

Физический маятник

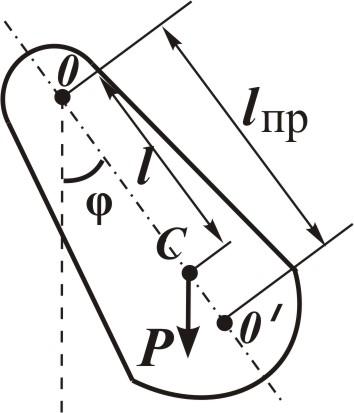
Рис. 4.1.

Физическим маятником называется любое твердое тело, способное совершать колебания вокруг неподвижной оси, не проходящей через его центр инерции.

На рис. 4.1 точка O – проекция оси вращения на плоскость рисунка, точка С – центр инерции, прямая проходящая через точку С и перпендикулярная оси вращения – ось маятника. l – расстояние от центра инерции до оси вращения. При отклонении маятника от положения равновесия на угол φ возникает вращающий момент, стремящийся вернуть маятник в положение равновесия. Момент силы тяжести численно равен . Подставив его значение в уравнение (4.1), получим:

(4.2)

Для малых углов (φ < 5⁰) справедливо – sin φ ≈ φ. Обозначив , получим уравнение:

(4.3)

Решением такого уравнения является функция вида φ =φ₀sinωt, это означает, что маятник будет совершать гармонические колебания с частотой ω. Соответственно период его колебаний будет равен:

(4.4)

Если сравнить это выражение с выражением для периода колебаний математического маятника^ (), то видно, что роль, аналогичную длине математического маятника, играет величина . Эту величину называют приведенной длиной физического маятника.

Таким образом, приведенной длиной физического маятника называется длина математического маятника с периодом колебаний, равным периоду данного физического маятника. Тогда из формулы (4.4) легко получить:

(4.5)

Если вдоль оси физического маятника от оси вращения (рис. 4.1) отложить расстояние равное приведенной длине, то полученная точка О' называется центром качания. Она обладает тем свойством, что период колебаний маятника относительно оси проходящей через эту точку будет таким же, как и относительно исходной оси.

Опираясь на это свойство, можно утверждать, что если периоды колебаний физического маятника относительно двух различных осей совпадают, то расстояние между ними равно приведенной длине физического маятника. На этом и основан используемый в данной работе метод (рис.  4.2).

период колебаний маятника относительно одной оси – , а относительно второй – . Здесь I₁ и I₂ - моменты инерции маятника относительно первой и второй осей, l₁ и l₂ – расстояния от центра инерции до двух осей, соответственно. По теореме Штейнера момент инерции тела относительно некоторой оси выражается через момент инерции I₀ относительно оси, проходящей через его центр инерции и параллельный данной: I =I₀ +ml². Тогда:

(4.6)

Возведя эти уравнения в квадрат, и вычтя второе из первого, получим: . если периоды равны, то это уравнение преобразуется к виду , что аналогично уравнению (4.5), если (l₁ + l₂) – приведенная длина.

Воспользовавшись формулами (4.6) при равенстве периодов легко получить выражения для моментов инерции:

I0 = ml1l2, I1 = ml1lприв и I2 = ml2lприв

(4.7)

Описание экспериментальной установки.

Рис. 4.2

Физический маятник, используемый в данной работе, представляет собой массивный стержень, на котором укреплены две опорные призмы и два дополнительных груза, выполненные в виде «чечевиц». (Рис. 4.2.)

Опорные призмы предназначены для подвешивания маятника на специальную опору двумя способами (прямое и оборотное положение) и жестко закреплены на стержне. Расстояние между призмами указано на рабочем месте. Одна из «чечевиц» также жестко закреплена, вторая может перемещаться вдоль стержня, ее положение фиксируется по шкале.

При перемещении «чечевицы» изменяется момент инерции маятника, а, следовательно, и период его колебаний.

Для измерения периодов колебаний маятника используется частотомер, соединенный с фотоэлементом.

Фотоэлемент укреплен перед маятником, а за маятником – лампочка. В неподвижном положении маятник перекрывает свет, идущий от лампочки к фотоэлементу. При колебаниях маятника такое перекрывание осуществляется два раза за один период колебаний. Частотомер установлен в режим, при котором фиксируется время 5-ти периодов.

Для определения центра инерции маятника служит настольная призма.

Порядок выполнения работы.

1. Включить лампочку и частотомер.

2. Убедиться в том, что свет от лампочки попадает на фотоэлемент при отсутствии маятника.

3. Убедиться в том, что частотомер настроен на необходимый режим и срабатывает при перекрывании света (с помощью преподавателя или дежурного сотрудника лаборатории).

4. Закрепить подвижную «чечевицу» в фиксированном начальном положении. (Например, 5 см по шкале маятника).

5. Подвесить маятник на одну из опорных призм. Привести его в колебательное движение (угол отклонения не более 5⁰). Измерить период колебаний Т₁ (не менее 3 раз).

6. Не изменяя положение подвижной «чечевицы», перевернуть маятник и подвесить его на другой опорной призме. Измерить период колебаний Т₂ (не менее 3 раз).

7. Закрепить подвижную «чечевицу» в новом фиксированном положении. (Например, 10 см по шкале маятника).

8. Повторить пункты 5 и 6.

9. Проанализировав значения Т₁ и Т₂, полученные при двух положениях чечевицы, определить (приблизительно) при каком ее положении ожидается совпадение периодов Т₁ и Т_2.

10. Закрепить подвижную «чечевицу» в предсказанном положении и повторить измерения Т₁ и Т₂. Сравнить полученные значения периодов с измеренными ранее и определить в какую сторону необходимо далее сдвигать «чечевицу» для сближения величины периодов.

11. Повторять измерения, сдвигая чечевицу в нужную сторону и анализируя значения периодов, до тех пор, пока не добьетесь наиболее точного совпадения периодов Т₁ и Т₂. (Подумайте, чем ограничена точность).

12. При найденном положении чечевицы, определить центр инерции маятника, положив его на настольную призму. Измерить расстояние от центра инерции до ближайшей опорной призмы.

Обработка результатов измерений

Из значений Т₁ и Т₂, полученных при том положении чечевицы, когда они наиболее близки, найти среднее значение периода Т и его погрешность. Определить значение g по формуле (4.5) и его погрешность по формуле:

Рассчитать моменты инерции маятника относительно осей проходящих через центр инерции и через ребра опорных призм по формулам (4.7).

Рассчитать погрешности моментов инерции маятника по формулам переноса ошибок (вывести самостоятельно)

Содержание отчета.

1. Характеристики измерительных приборов.

2. таблица экспериментальных данных.

Примерный вид таблицы

Положение чечевицы, см	№ опыта	Т1	Т2	Результат сравнения T1 и T2
	1
	2
	3
	1
	2
	3
	1
	2
	3

3. Значения l_прив , l₁ и l₂

4. График зависимости Т₁ и Т₂ от положения чечевицы (по указанию преподавателя).

5. Вычисленные значения g и его погрешности.

6. Вычисленные значения моментов инерции и их погрешностей.

Контрольные вопросы

• Что такое приведенная длина физического маятника?

• Каким образом в данной работе определяется приведенная длина?

• Почему ускорение свободного падения зависит от широты?

• В какой точке Земли g - максимально, а в какой точке - минимально?

 Математическим маятником называется идеализированная система, состоящая из невесомой нерастяжимой нити на которой подвешена масса, сосредоточенная в одной точке.

8