САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета сПбГу

Часть IV электричество

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Санкт-Петербург 2007

ББК 22.33

Печатается по постановлению Ученого совета физического факультета СПбГУ.

Ответственные редакторы:В.И. Коротков, Е.П. Зароченцева

Авторы:А.В. Бармасов, И.С. Бобкова, С.О. Высоцкая, Б.Д Катунин, Т.Н. Компаниец, Т.К. Крутицкая, Н.А. Малешина, Т.В. Рудакова,В.Е. Тер-Нерсессянц

Составитель:Т.В. Рудакова

Рецензент:кандидат.физ.-мат. наук, снс, Л.Л. Басов (СПбГУ)

Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета СПбГУ. ЧастьIV: Электричество. Постоянный электрический ток / А.В. Бармасов, И.С. Бобкова, С.О. Высоцкая и др.;

Под ред. В.И. Короткова, Е.П. Зароченцевой;

СПб., 2007. – 93 с.

Данное пособие содержит описания лабораторных работ по разделу «Электричество. Постоянный электрический ток» курса общей физики и представляет собой существенно переработанное и дополненное переиздание учебного пособия «Электричество (постоянный ток). Ч. 4. / Под ред. В.Е. Холмогорова и Ю.Г. Шишкина» (Л.: Изд-во ЛГУ, 1988. –104 с.). Каждая лабораторная работа рассчитана на 4 академических часа. Студент допускается к выполнению лабораторной работы после самостоятельного изучения необходимой теории, ознакомления с порядком выполнения основных операций и сдачи зачёта по технике безопасности. Предназначено для студентов факультетов: биолого-почвенного, географии и геоэкологии, геологического, медицинского, физического, химического и др.

ББК 22.33

Ó А.В. Бармасов,

И.С. Бобкова,

С.О. Высоцкая и др., 2007

Ó Санкт-Петербургский

государственный

университет, 2007.

СОДЕРЖАНИЕ

1. Электроизмерительные приборы	4
Классификация электроизмерительных приборов	4
Определение погрешности измерения на электроизмери-тельных приборах. Класс точности прибора.	7
Масштабные измерительные преобразования (МИП)	10
Лабораторная работа 31 Исследование проводников 1-го рода с помощью моста постоянного тока	14
Лабораторная работа 32 Определение ЭДС и напряжений методом компенсации	21
Лабораторная работа 33 Определение емкостей конденсаторов и ЭДС гальванических элементов при помощи гальванометра	30
Лабораторная работа 34 Изучение закономерностей прохождения электронов в вакууме. Закон степени трех вторых. Определение удельного заряда электрона	38
Лабораторная работа 35 Изучение работы трехэлектродной лампы	44
Лабораторная работа 36 Изучение работы однолучевого электронного осциллографа С1-54	54
Лабораторная работа 38 Определение удельного заряда электрона методом магнитной фокусировки электронного пучка	75
Лабораторная работа 39 Определение горизонтальной составляющей магнитного поля Земли.	83
Приложения
Аналоговые электроизмерительные приборы	89
Краткая характеристика электроизмерительных приборов наиболее распространенных систем	92
Литература	93

ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

Измерение– это нахождение опытным путём с оцененной точностью значения заранее выбранной физической величины путем сравнения ее с эталонной величиной. Электрические измерения осуществляются с помощью электроизмерительных приборов (ЭИП).

Объектами электрических измерений могут быть как электрические и магнитные величины, так и неэлектрические величины (такие, например, как давление, скорость, температура). Для того чтобы измерить неэлектрическую величину с помощью электроизмерительных приборов, ее надо преобразовать в зависящую от нее электрическую величину. Устройства для измерения неэлектрических величин должны содержать преобразователь, соединительные провода и электроизмерительный прибор, шкала которого проградуирована в единицах измеряемой величины.

В качестве одного из наиболее простых примеровможно привести измерение температуры с помощью термопары. Величина электродвижущей силы (эдс)термопары зависит от разности температур между горячим и холодным спаями, т. е. термопара является в данном случае преобразователем. С помощью проводов к ней подключается милливольтметр, измеряющийэдстермопары (термоЭДС). В этом случае шкалу милливольтметра можно проградуировать в единицах температуры.

Классификация электроизмерительных приборов

ЭИП можно классифицировать по различным признакам:

По характеру снимаемых показаний измеряемой величины.

Показывающие ЭИП. Это приборы, предварительно отградуированные и позволяющие производить по шкале отсчет численного значения измеряемой величины. С помощью таких приборов можно сразу получить значение измеряемой величины.

Регистрирующие ЭИП.Эти приборы допускают считывание и регистрацию или только регистрацию показаний. К таким приборам относятся самопишущие приборы, дающие запись показаний в виде диаграммы, печатающие приборы, которые печатают показания в цифровой форме, а также осциллографы. Для получения значений измеряемой величины такие приборы требуют специальной градуировки.

По способу преобразования измеряемой величины и способу считывания показаний.

Аналоговые ЭИП.В этих приборах показания являются непрерывными функциями изменений измеряемых величин.

Примером аналогового прибора может служить стрелочный амперметр (рис. 1).

Рис. 1.

При увеличении тока стрелка амперметра смещается плавно. Тем не менее, плавность изменения показаний не означает, что величина тока может быть измерена с любой точностью (см. ниже).

Цифровые приборы. В таких приборах непрерывно изменяющийся измеряемый параметр преобразуется в дискретный параметр (число), которое отображается на его отсчетном устройстве – панели цифровой индикации (рис. 2).

Рис. 2.

При плавном изменении тока показания прибора изменяются дискретно.

Приборы сравнения.Это приборы, предназначенные для непосредственного сравнения измеряемой величины с величиной, значение которой известно. К таким приборам относятся, например, мосты, потенциометры, компенсаторы напряжения и тока.

Простейшим примером схемы сравнения может служить компенсатор напряжения. Принцип работы компенсатора напряжения показан на рис. 3.

Рис. 3.

ЭДС источников равны, когда показание гальванометра равно нулю. Основное достоинство такого способа измерения состоит в том, что в этом случае не происходит отбора тока от источника. Этот способ удобен для измерения ЭДС источников с большим внутренним сопротивлением.

Особенно хорошо видны преимущества методов сравнения при измерении сопротивлений. Можно определить сопротивление, воспользовавшись амперметром и вольтметром (R=U/I). Такой способ (способ амперметра и вольтметра) является наиболее простым, но наименее точным из-за присущей ему систематической ошибки.

Два варианта включения измерительных приборов показаны на рис. 4. На рис. 4,априведена схема «правильная по напряжению», но амперметр показывает сумму токов, текущих через вольтметр и нагрузку. На рис. 4,б– схема «правильная по току», но вольтметр показывает сумму падений напряжения на амперметре и нагрузке.

Рис. 4.

Широкое применение для измерения сопротивлений получили мосты, питаемые постоянным током, так как их уравновешивание несложно и подбор подходящего гальванометра не составляет особого труда.

Примеромтакой схемы сравнения может служить четырёхплечевой мост постоянного тока, применяемый для измерения сопротивлений (рис. 5).

Рис. 5.

В одно из плеч моста включен неизвестный резистор R_X. При измерении сопротивления таким методом, неизвестное сопротивление сравнивается с известными сопротивлениями моста, а включенный в одну из диагоналей моста гальванометр Г служит индикатором отсутствия тока.

Точность измерения в данном случае определяется точностью значений известных сопротивлений и чувствительностью гальванометра.

Мосты переменного тока применяются, в основном, для измерения индуктивностей и емкостей.

Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора

Следует помнить, что никакое измерение, т. е. сравнение с эталонной величиной, не может быть выполнено абсолютно точно. Результат измерения всегда содержит некоторую ошибку. Кроме того, надо учесть, что измерение проводится не путем сравнения с самим эталоном, а с помощью измерительного прибора (который при поверке сравнивается с эталоном). Очевидно, что, измеряя с помощью этого измерительного прибора, мы не можем сделать ошибку меньше, чем та, которая определяется погрешностью измерительного устройства.

Разность между показаниями прибора и действительным значением измеряемой величины называется абсолютной погрешностьюDА.

DА=êАИЗМ–АДЕЙСТê.

(1)

Отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в процентах, называется относительной погрешностью:

.

(2)

Приведенные определения относительной и абсолютной погрешности не дают возможности узнать их величину, так как действительное значение измеряемой величины нам неизвестно. Определить величины погрешностей при электрических измерениях становится возможным, если известен класс точностиприбора (g_КЛ.Т.). Он дает предельную абсолютную погрешность, выраженную в процентах, от номинального показания прибора (максимального при данном пределе измерения)А_НОМ:

.

(3)

Класс точности указан на шкале прибора (см. Рис. 6).

Зная класс точности прибора, можно легко определить абсолютную погрешность измерения DА:

.

(4)

Например, для катушки сопротивления в 1000 Ом класса точности 0,05 абсолютная погрешность:

.

Относительную погрешность также можно вычислить через класс точности прибора. По определению относительная погрешность:

.

(5)

Учитывая, что действительное значение измеряемой величины А_ДЕЙСТи показания прибораА_ИЗМпримерно равны (А_ДЕЙСТ»А_ИЗМ), и, используя формулу (4), получим:

.

(6)

Видно, что относительная погрешность измерений будет тем меньше, чем ближе снимаемые показания к номинальному значению для данного прибора, то есть к концу шкалы. Следовательно, при работе с многопредельными ЭИП нужно так выбирать предел измерения прибора, чтобы показания считывались со второй половины шкалы. Следует помнить, что номинальное значение многопредельного ЭИП определяется положением, в котором стоит переключатель пределов при данном измерении.

При работе с многопредельными приборами нужно внимательно рассчитывать цену одного деленияшкалы Ц_Д. Под ценой деления следует понимать не разность между штрихами, а разность между нимив соответствии с оцифровкой шкалы.Цена деленияравномерной шкалы равна отношению номинального значения показания прибора (предела измерения) к общему числу деленийNна шкале прибора: Ц_Д=. Численное значение измеряемой величиныА_ИЗМравно цене деления Ц_Д, умноженной на измеренное число деленийN_ИЗМпо шкале:

АИЗМ= ЦД·NИЗМ.

(7)

Рассмотрим примеры определения погрешностей для многопредельных ЭИП.

Пример 1.
Переключа-тель пределов измерения	→		← ←	Шкала прибора Класс точности gКЛ.Т.(0,5)
Рис. 6.

На рис. 6 изображён многопредельный вольтметр. Вычислим абсолютную и относительную погрешности определения напряжения. Класс точности вольтметра 0,5.

Номинальное значение напряжения 300 В (определяется положением переключателя пределов напряжения).

Цена деления данного предела измерения Ц_Д== 2 В/дел.

Измеренное значение напряжения U_ИЗМ= 2 В/дел.·75 дел. = 150 В.

Абсолютная погрешность измерения DU== 1,5 (В).

Относительная погрешность измерения g₀== 1,0%.

Пример 2. Рис. 7.

На рис. 7 изображен тот же многопредельный вольтметр при другом положении переключателя пределов измерений. Вычислим абсолютную и относительную погрешности определения напряжения.

Номинальное значение напряжения 150 В.

Цена деления данного предела измерения Ц_Д= 150 В / 150 дел. = 1 В/дел.

Измеренное значение напряжения U_ИЗМ= 1 В/дел.×150 дел. = 150 В.

Абсолютная погрешность измерения DU== 0,75 (В).

Относительная погрешность измерения ₀== 0,5%.

Таким образом, выбор наиболее подходящего предела измерения приводит к уменьшению как абсолютной, так и относительной погрешности.

Масштабные измерительные преобразователи (МИП)

При необходимости измерения токов и напряжений, превышающих верхний предел измерения используемого прибора, используются МИПы.

Для приборов постоянного тока в качестве МИП используются шунты и добавочные сопротивления. Для приборов переменного тока - добавочные резисторы и измерительные трансформаторы тока и напряжения.

Расчёт шунта к амперметру

При измерении тока амперметр включается последовательно с нагрузкой. Если амперметром требуется измерить ток, превышающий верхний предел измерения, то параллельно амперметру включается шунт с сопротивлением R_Ш(рис. 8).Шунтпредставляет собой толстую константановую или манганиновую пластину. Применение этих сплавов для изготовления шунтов связано с тем, что их сопротивление слабо зависит от температуры.

Рис. 8.

На рис. 8 показана схема подключения шунта R_Шк амперметру.R_А– внутреннее сопротивление амперметра, которое мало по сравнению с сопротивлением нагрузкиR_Ндля того, чтобы включение амперметра последовательно с нагрузкой не приводило к существенным изменениям тока в цепи нагрузки.I– ток через сопротивление нагрузкиR_Н;I_Ш– ток через шунт с сопротивлениемR_Ш;I_А– ток через амперметр с сопротивлениемR_А.

По первому правилу Кирхгофа алгебраическая сумма токов в узле равна нулю:

I=I_А+I_Ш

и, следовательно,

I_Ш=I–I_А.

Падение напряжения между точками аиb:

U_аb=I_А·R_А=I_Ш·R_Ш.

Таким образом, для того, чтобы с помощью данного амперметра измерить ток I, сопротивление шунта должно быть:

,

(8)

где: I/I_A=n–коэффициент шунтирования, показывающий, во сколько раз расширяется предел измерения амперметра при подключении шунта.

Фактический ток в цепи определяется произведением показаний прибора и множителя n.

Рис. 9.

Реальный шунт (рис. 9) должен иметь четыре контакта: к двум из них подключается прибор, а к двум другим – соединительные провода электрической цепи.

Пример 3.

Рассчитаем шунт к миллиамперметру на 10 mА с внутренним сопротивлением 500 Ом, если надо измерить ток 10 А.

Воспользуемся формулой (8):

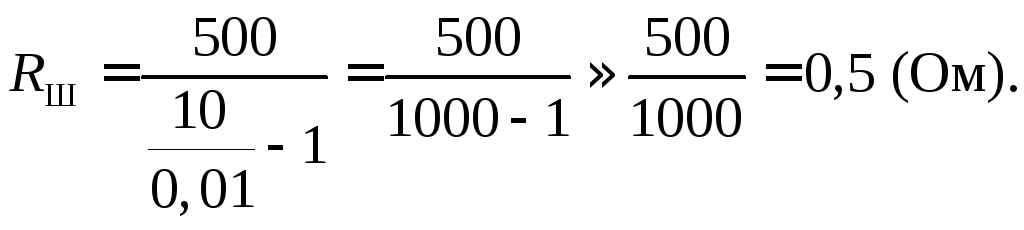
Расчёт добавочного сопротивления к вольтметру

Для измерения напряжения вольтметр включается параллельно с нагрузкой. Если вольтметром требуется измерить напряжение, превышающее верхний предел измерения, то последовательно вольтметру включают добавочное сопротивление R_Д.

Рис. 10.

На рис. 10 показана схема подключения добавочного сопротивления R_Дк вольтметру.R_V– внутреннее сопротивление вольтметра. Оно должно быть большим по сравнению с сопротивлением нагрузкиR_Ндля того, чтобы включение вольтметра параллельно нагрузке не приводило к существенным изменениям напряжения на нагрузке.U_ИЗМ– измеряемое напряжение;U_НОМ– предел измерения вольтметра.

Ток, текущий через вольтметр:

,

следовательно, добавочное сопротивление должно быть:

.

(9)

Пример 4.

Рассчитаем добавочное сопротивление к вольтметру на 100 В для измерения напряжения 300 В. Внутреннее сопротивление вольтметра R_V= 3000 Ом.

.

Добавочные сопротивления могут служить и для преобразования рода измеряемой величины (напряжения в ток и наоборот). Рассмотрим, как измерить напряжение с помощью амперметра. Для этого последовательно с амперметром включается большое сопротивление R_Д(рис. 11).

Рис. 11.

Неизвестное напряжение U_X=I_А·(R_Д+R_А), гдеR_А– внутреннее сопротивление амперметра. Если величины внутреннего и добавочного сопротивлений известны, то, измеряя ток с помощью амперметра, легко вычислить искомое напряжение.

Читайте также раздел «Приложения».

Лабораторная работа 31

ИССЛЕДОВАНИЕ ПРОВОДНИКОВ I–го РОДА С ПОМОЩЬЮ МОСТА ПОСТОЯННОГО ТОКА

Задачи работы

1. Определение сопротивления проводников с помощью моста постоянного тока.

2. Расчет удельного сопротивления проводников.

Физическое обоснование эксперимента

Электрический ток в металлах – проводниках 1-го рода – обусловлен направленным (упорядоченным) движением электронов под действием приложенного электрического поля. Электроны в металлах считаются «свободными» из-за сравнительно слабой связи с ионами кристаллической решетки, внутри которой они могут свободно перемещаться.

Для создания и поддержания упорядоченного движения заряженных частиц необходимо электрическое поле. Если внутри проводника имеется электрическое поле, то между концами проводника существует разность потенциалов ∆φ, именуемая также напряжением.

Заряд, перенесенный в единицу времени, служит основной количественной характеристикой тока, называемой силой тока.

Сила тока I, текущего по однородному металлическому проводнику, согласно закону Ома пропорциональна напряжениюU на проводнике (разности потенциалов электрического поля), приложенному к концам проводника:

, (31.1)

где – электрическое сопротивление проводника.

Величина сопротивления зависит от геометрической формы и размеров проводника, а также от свойств материала, из которого он сделан. Для длинного проводника с круглым сечением

, (31.2)

где – площадь его поперечного сечения, а ρ – коэффициент, зависящий от свойств материала, называемый удельным электрическим сопротивлением,– длина проводника. При= 1 м и= 1 м²,R = ρ, т. е. коэффициент ρ численно равен сопротивлению проводника единичной длины и единичного поперечного сечения. В системе СИρизмеряется в ом-метрах (Ом·м). Величина σ = 1/ρ называется удельной электрической проводимостью и выражается в сименсах на метр (См/м).

Какова физическая природа электрического сопротивления R?

Согласно классической теории электроны проводимости в металлах ведут себя как частицы идеального газа. Двигаясь упорядоченно, они взаимодействуют (упруго сталкиваются) с положительными ионами в узлах кристаллической решетки, и изменяют направленность своего движения (рассеиваются).

Однако классическая теория натолкнулась на трудности в вопросе о теплоемкости электронного газа. Кроме того, экспериментально наблюдаемая пропорциональность удельного сопротивления ρ температуре также не могла быть объяснена с классической точки зрения.

Эти проблемы были преодолены в квантовой механике, которая рассматривает движение электрона как распространение волны. Электронные волны рассеиваются на неоднородностях, всегда существующих в кристаллической решетке. В случае идеальной решетки неоднородности, рассеивающие волны, связаны лишь с тепловым движением (колебаниями) решетки, что ведет к пропорциональности удельного сопротивления ρ температуре кристалла t.При наличии примесей в кристаллической решетке имеются неоднородности, не зависящие от температуры, поэтому связь удельного сопротивления ρ с температурой принимает вид:

,

где ρ₀ – значение удельного сопротивления металла при температуреt → 0⁰ C, – температура, α – температурный коэффициент сопротивления.

Для большинства металлов при температурах, близких к комнатной, ρ изменяется пропорционально температуре. При низких температурах наблюдается отступление от этой закономерности.

Если известно сопротивление Rоднородного цилиндрического проводника диаметромdи длинойL, то расчет удельного сопротивления ρ производится по формуле:

, (31.3)

Существуют несколько способов измерения R:

а) прямое измерение омметром;

б) косвенное измерение с помощью других электроизмерительных приборов, например, вольтметра и амперметра ;

в) измерение с помощью моста постоянного тока, называемого также мостом Уитстона. Мостовой метод является наиболее точным, так как позволяет исключить погрешности, вносимые омметром и иными приборами. Подробнее о погрешностях электроизмерительных приборов можно прочитать в разделе «Электроизмерительные приборы».

Измерение сопротивления проводников с помощью моста постоянного тока

Рассмотрим принципиальную схему четырехплечевого моста постоянного тока. Четыре сопротивления (четыре плеча)R₁,R₂,R₃,R₄, соединены в четырехугольникADBC(рис. 31.1). СопротивлениеR₄ =R_Xявляется измеряемым, остальные три известны, причем, по крайней мере, одно из них (в данном случаеR₃) является регулируемым. В одну из диагоналей мостаABвключен источник питания, во вторую – магнитоэлектрический нулевой индикатор – обычно гальванометр Г. Гальванометр является высокочувствительным прибором, предназначенным для измерений очень малых токов (менее 10^–6А).

Меняя величину регулируемого сопротивления, можно добиться такого состояния схемы, при котором напряжение (разность потенциалов) между точками CиD, и, следовательно, ток в гальванометре Г равны нулю. Это состояние называют состоянием равновесия моста (мост сбалансирован).

Состояние равновесия наступает только при определенном соотношении плеч моста – сопротивлений R₁,R₂,R₃,R₄.

Обозначим I₁,I₂,I₃,I₄ – силу токов, текущих по соответствующим плечам, ток через гальванометр –I_Г, а потенциалы в точкахA, B, C, D –V_A,V_B,V_C,V_D. Если мост сбалансирован, тоI_Г= 0. Это возможно при условии, что потенциалы в точкахCиDодинаковы. Значит, в случае баланса моста имеем:

φ_С = φ_D.(31.4)

По закону Ома имеем:

I₁ = (φ_A – φ_D)/R₁, I₂ = (φ_D – φ_B)/R₂,

I₄ = (φ_A – φ_C)/R₄, I₃ = (φ_C – φ_В)/R₃,

Разделив I₄наI₁, аI₃наI₂, с учетом равенства (31.4) получим:

. (31.5)

Таким образом, если ток в гальванометре отсутствует, то неизвестное сопротивление R_X=R₄можно выразить через три другие сопротивления

, (31.6)

где R₃ – сопротивление в плече сравнения,R₁иR₂ – сопротивления плечей отношения. Из (31.6) видно, что измерение сопротивленияR_Xсводится к регулировке плеча сравненияR₃при постоянном отношении, (либо к регулированию отношенияпри постоянном значенииR₃) до исчезновения токаI_Гв гальванометре. При этомR_Xявляется сопротивлением всего плеча моста, ограниченного узламиAиC, включая сопротивления соединительных проводов и сопротивления всех контактов между этими точками. Если измеряемое сопротивлениеR_Xмного больше сопротивления проводов и контактов (которые трудно сделать меньше нескольких тысячных долей Ома), то измерениеR_Xможет быть произведено с достаточно высокой точностью. Однако, еслиR_Xмало (меньше 1 Ом), то погрешность определенияR_Xвелика, и надо применять более сложные мостовые схемы. При измерении больших сопротивлений (больше 100 кОм) погрешности возможны из-за токов утечки, которые могут появляться вследствие соизмеримости сопротивлений изоляции моста и измеряемого сопротивления. Поэтому большие сопротивления измеряют с помощью других методов. Четырехплечевой мост постоянного тока обычно применяется для измерения сопротивлений в пределах от 1 Ом до 100 кОм.

Метод измерений сопротивлений с помощью моста – это метод сравнения или нулевой метод: неизвестное сопротивление сравнивается с известным, а гальванометр служит индикатором отсутствия тока в диагонали моста. Следовательно, точность измерения обусловлена точностью изготовления известных сопротивлений и чувствительностью гальванометра (чувствительностью моста).

Можно показать, что чувствительность моста максимальна, когда , т. к. при этом погрешность измеренияR_X – минимальна.

Описание экспериментальной установки

В работе используется четырехплечевой реохордный мост (рис. 31.2). В нем плечи отношенияивыполнены в виде реохордаADB – однородного калиброванного провода неизменного сечения, по которому перемещается контактD, являющийся одним из узлов моста. Длина реохордаl = 1 м, и натянут он вдоль миллиметровой линейки. Скользящий контактD(ползунок) с выключателем К₂может быть снабжен нониусом. Гальванометр Г включен в диагональ мостаCD. Источник питания Ε и ключ К₁включены в диагональAB.R_X – измеряемое сопротивление,R₃ =R₀ – эталонное сопротивление (в виде магазина сопротивлений).Пока мост не сбалансирован ключ К₂ замыкается лишь на очень короткое время во избежание длительного протекания через него больших токов!

Для реохорда отношение R₁/R₂равно отношению длин соответствующих отрезков проволокиl₁иl₂=l–l₁:

и. (31.7)

Исследуемые проводники R_Xнатянуты на деревянном столбике и их концы выведены на клеммы, длина проволокуказана на основании столбика.

Порядок выполнения работы

1. Собрать схему (рис. 31.2).

2. После проверки схемы моста замкнуть ключ К₁, установить ползунокDна середине реохорда и, подбирая различные значенияR₀на магазине сопротивлений, добиться того, чтобы ток через гальванометр Г был минимальным.

Подбирать R₀нужно методом «ножниц», который основывается на том, что пристрелка гальванометра отклоняется в одну сторону, при– в другую. Метод заключается в следующем. Установить на магазине сопротивлений заведомо малое сопротивление (R₀= 0 Ом). Замкнуть ключК₂. Заметить, в какую сторону отклоняется стрелка гальванометра. РазомкнутьК₂. Выставить заведомо большое сопротивление (по указанию преподавателя). Убедиться, что стрелка гальванометра отклоняется в другую сторону. Задать промежуточное значение плеча сравнения (например,R₀= 5 Ом). По отклонению стрелки определить является это значение большим, чемR_x,или меньшим. В зависимости от этого уменьшить или увеличить величинуR₀. В дальнейшем следует прибавлять или убавлять целые или десятые доли Ом до тех пор, пока отклонение стрелки гальванометра не станет минимальным. При этомвключать лишь на очень короткое время (чтобы только заметить, в какую сторону отклоняется стрелка гальванометра).

Точно сбалансировать мост только подбором R₀невозможно из-за конечности минимального значения (шага), на которое его можно изменить. Это минимальное значение для магазина сопротивлений, используемого в данной работе, равняется 0,1 Ом.

3. Произвести точную балансировку моста (), передвигая ползунокDвблизи середины реохорда, т. е. меняя отношение. Определить величину плечаl₁.

4. Повторяя процедуру балансировки при подобранном сопротивлении(наиболее близком к), получить 5 значений плечаl₁.

5. Измерить микрометром диаметр dисследуемой проволоки в 5 различных местах.

6. Повторить все описанные измерения еще для 2-х различных проволок.

Обработка результатов измерений

В случае, если разброс данных превышает погрешность линейки реохорда и микрометра, границы доверительных интервалов ∆l₁и Δdнаходят по алгоритму прямых измерений. Относительные погрешности=и рассчитывают по формулам погрешности косвенных измерений:

,

где ,– класс точности магазина сопротивлений, указанный на приборе.

,

Доверительные интервалы искомых величин определяются, соответственно: ; ∆.

Окончательный результат представить в виде

Ом,Ом∙м.

Вычисления произвести для всех исследованных проводников.

Результаты измерений и расчеты рекомендуется записать в таблицу:

Материал, из которого изготовлена проволока	Ом	Номер опыта	см	см	мм	мм	Ом	Ом∙м
Три варианта различных проволок.

Содержание отчёта

1. Электрическая схема измерений сопротивлений проводников.

2. Сводная таблица экспериментальных данных.

3. Расчёт трех сопротивлений проводников по формуле (31.7).

4. Расчёт удельных сопротивлений проводников по формуле (31.3).

5. Расчёт границ доверительных интервалов (абсолютной погрешности) измерения трех сопротивлений проводников и их удельных сопротивлений.

Контрольные вопросы

• От чего зависит величина удельного сопротивления однородного проводника?

• Если мост сбалансирован, то по каким плечам моста (см. рис. 31.1) будут течь равные токи? Почему нельзя надолго замыкать ключ К₂в схеме на (рис. 31.2)?

• Почему следует работать на середине реохорда АВ(рис. 31.2) при балансировке моста?

Лабораторная работа 32

ОПРЕДЕЛЕНИЕ ЭДС И НАПРЯЖЕНИЙ КОМПЕНСАЦИОННЫМ МЕТОДОМ

Задачи работы

1. Определение ЭДС элемента при комнатной температуре компенсационным методом.

2. Определение внутреннего сопротивления элемента.

Физическое обоснование эксперимента

Закон Ома для полной цепи

Согласно закону Ома для полной цепи электродвижущая сила (ЭДС) источника тока равна сумме падений напряжения на внешнем и внутреннем участках цепи:

,

где I – ток в цепи,R– сопротивление внешней цепи,– внутреннее сопротивление источника тока,E – ЭДС источника тока. ЕслиR>>r,то напряжение во внешней части цепи приближается по своему значению к ЭДС источника:E ≈ IR. Отсюда следует, что ЭДС равна разности потенциалов между полюсами разомкнутого источника тока. Поэтому для измерения ЭДС источника тока необходимо применить метод, при котором ток в цепи источника отсутствует, например метод компенсации.

Определение ЭДС методом компенсации

Сущность метода компенсации ЭДС состоит в следующем. Рассмотрим принципиальную электрическую схему, представленную на рис. 32.1. Источник тока с ЭДС Eподключается к реохордуAB, а исследуемый элемент с ЭДСE_x присоединяют к началу реохордаAи через чувствительный гальванометрГ к подвижному контакту реохордаС. При этомнеобходимо выполнить два условия: 1) ЭДС элементаEдолжна быть больше ЭДС элементаE_х, 2) к точкеАреохорда элементы подключаются одинаковыми полюсами.

Так как Е > Е_x, то на реохордеАВвсегда будет такая точка, разность потенциалов между которой и точкойАбудет равна электродвижущей силе исследуемого элемента. Перемещая контактСвдоль реохорда, ищут такое его положение, при котором в контуреAFГСс элементомЕ_xтока не будет. При этом происходиткомпенсацияпадения напряжения на участкеАСреохорда и подключенной к этому участку электродвижущей силыЕ_x.

Отсутствие тока в гальванометре становится возможным только при соединении источников ЭДС в схеме одноименными полюсами. В этом случае ток I₂, который ответвился бы в контурAFГСпри отсутствии в нем элементаЕ_x,и токI₁, индуцированный элементомЕ_x, текут в противоположных направлениях. ТокI₂– от “плюса” (точкаА) через точкиFиГк “минусу” (точкаС), т.е. против часовой стрелки. ТокI₁– от “плюса” к “минусу” элементаЕ_x, т.е. по часовой стрелке). При компенсации токиI₁иI₂становятся равными по величине, и суммарный ток через гальванометр не идет.

При условии, что ЭДС Е_xскомпенсирована, токIв контуреAODBне разветвляется и равен:

, (32.1)

где R_AODB– полное сопротивление контураAODB.Обозначимr_xсопротивление участка цепи между точкамиАиС. Тогда разность потенциаловV_A - V_Cмежду точкамиАиС:

. (32.2)

Следовательно, электродвижущая сила Е_xисследуемого элемента равна:

. (32.3)

Если заменить исследуемый элемент нормальным элементом Вестона, электродвижущая сила Е_nкоторого известна, и вновь добиться отсутствия тока в контуреAFГС, можно получить:

. (32.4)

Разделив выражение (32.3) на выражение (32.4), имеем:

. (32.5)

Таким образом, сравнение электродвижущих сил двух элементов может быть практически сведено к сравнению двух сопротивлений, использованных при компенсационных измерениях.

Метод компенсации для определения ЭДС обладает рядом важных преимуществ. Во-первых, сила тока через элементы, ЭДС которых сравниваются между собой, близка к нулю. Точность измерений ограничивается ценой деления гальванометра, которая соответствует 10^-6– 10^-7 А у различных типов стрелочных гальванометров. Поэтому падения напряжения внутри элемента, снижающего значение измеренной на полюсах элемента разности потенциалов, практически нет. Не существенным является и падение напряжения в проводах, соединяющих элемент с измерительной схемой. Во-вторых, при компенсационном методе гальванометр работает как нулевой прибор и градуировка его шкалы в результат измерений не входит. Наконец, величина ЭДС вспомогательной батареиЕтакже не входит в окончательный результат. Необходимо лишь, чтобы величина ее ЭДС во время измерений была постоянной. Рабочая схема для измерения ЭДС источника напряжения методом компенсации показана на рис. 32.2.

Она состоит из трех контуров, в каждый из которых включен источник напряжения. Контур AODBсостоит из источника напряженияE, ключаK1 и струны реохордаAB (длинной проволоки с большим удельным сопротивлением). При замыкании ключаK1элементЕподключается к реохорду. В контуреAMNCвключено большое сопротивлениеR0(порядка 105 Ом), нормальный элементEn, ЭДС которого известна с большой степенью точности, двойной ключK2 и чувствительный нуль-гальванометрГ.

Рис.32.2

В контур APQNCвключены сопротивлениеR₀, источникE_x, величину ЭДС которого следует измерить, ключK₂и гальванометрГ. КонтактCможет свободно перемещаться по струне реохорда.

Ключ K₂при замыкании может находиться либо в положении 1, тогда в цепь включается элементE_n , либо в положении 2, тогда в цепь включается исследуемый источникE_x.

Большое сопротивление R₀ необходимо включать в схему по следующей причине. Если в цепь включается нормальный элемент Вестона, то этот источник напряжения сохраняет неизменной свою ЭДС с точностью до шестого знака (при постоянной температуре) только в том случае, когда через источник течет ток, не превышающий 10^-4А. В противном случае нормальный элемент поляризуется и его ЭДС уменьшается. Кроме того, большое сопротивлениеR₀служит для защиты чувствительного гальванометраГот слишком больших токов при включении его в момент сильной раскомпенсации схемы.

Рассмотрим процесс измерения ЭДС по схеме рис. 32.2. Ключ K₂включен в положение 1. При этом в схему включается нормальный элемент. Перемещая контактCвдоль струны реохорда, добиваются отсутствия тока в гальванометре. Гальванометр имеет свой ключК_г .Включать этот ключ надо на очень непродолжительное время, чтобы убедиться, что компенсация в схеме еще не достигнута. При достижении компенсации ЭДС нормального элемента будет в точности равна падению напряжения на участке струны реохордаAC, сопротивление которого мы обозначимr_n.

Переключим теперь ключ K₂в положение 2. Этим самым мы включаем в цепь измеряемый источник напряженияE_x. Передвигая контактCна реохорде, необходимо добиться компенсации ЭДСE_xна новом сопротивленииr_x.

Если струна реохорда однородна, то и, где– удельное сопротивление струны реохорда, аS –площадь его поперечного сечения. В этом случае равенство (32.5) приобретает вид:

(32.6)

Таким образом, измерение ЭДС сводится к измерению длин иучастков струны реохорда, на которых выполняется компенсация.

Определение внутреннего сопротивления источника ЭДС методом компенсации

При помощи компенсационной схемы можно определить внутреннее сопротивление r₀исследуемого источника ЭДС. Для этого

параллельно элементу с неизвестной ЭДС включают внешнее сопротивление R1(рис. 32.3). Тогда при разомкнутом ключеK4мы имеем схему рис. 32.2, и при компенсации измеряем ЭДС элементаEх. Если же ключK4замкнут, то при компенсации измеряется падение напряженияUна внешнем сопротивленииR1. Закон Ома для полной

цепи, изображенной на рис. 32.3, можно записать в таком виде: , где, откуда; ; ток ;. Таким образом, внутреннее сопротивление источника токаЕ_х будет определяться по формуле

. (32.7)

Аналогично выводу формулы (32.5) можно получить выражение для U:

,

где r_U– сопротивление участка реохордаАС, на котором произошла компенсация напряженияU. Следовательно, выражение (32.7) приобретает вид:

. (32.8)

Компенсационные схемы могут быть использованы для градуировки различных электроизмерительных приборов – вольтметра, миллиамперметра, термопары.

Компенсационные методы широко применяются для измерения параметров электрических цепей. Характерной особенностью этих методов являются их простота и высокая точность.

Метод исследования и описание установки

Постановка экспериментальной задачи

В этой работе необходимо измерить компенсационным методом ЭДС трех элементов и внутреннее сопротивление одного из них.

Описание экспериментальной установки

Электрическая схема установки приведена на рис. 32.4. Реохорд ABв схеме рис.32.4 состоит из длинной нейзильберовой проволоки, намотанной на изолированный цилиндр. Параллельно образующей цилиндра помещена ось, на которой находится контактное колесико. На ось действует пружина, прижимающая колесико к виткам проволоки реохорда для

создания хорошего электрического контакта. Около колесика имеется шкала, по которой можно определить целые обороты цилиндра. Указателем числа оборотов является само колесико. Десятые и сотые доли оборота определяют по шкале, имеющей 100 делений, и расположенной у края барабана реохорда. Поэтому в момент компенсации схемы записывается не длина реохорда , а число оборотов цилиндра реохорда. Поэтому формула (32.6) для измерений ЭДС будет иметь вид:

, (32.9)

где – ЭДС нормального элемента,n_х– число оборотов реохорда в момент компенсации неизвестной ЭДС,n_n– число оборотов реохорда при компенсации нормального элемента. ЭлементЕслужит для питания реохорда,– нормальный элемент,Е_х –элемент с неизвестной ЭДС, которую необходимо определить,– охранное сопротивление (Ом),К₁ –кнопка включения гальванометра,Г– гальванометр,и– ключ и сопротивление для определения внутреннего сопротивления измеряемого элемента.

Нормальный элемент Вестона

Насыщенный нормальный элемент представляет собой запаянный стеклянный сосуд Н-образной формы (рис. 32.5) с впаянными в дно каждой из его ветвей платиновыми электродами, которые служат выводами ЭДС элемента. Положительным электродом служит чистая ртуть 1, заполняющая нижнюю часть одной из ветви сосуда. Отрицательным электродом 2 служит амальгама кадмия, заполняющая нижнюю часть второй ветви.

Над ртутью находится слой пасты – деполяризатора 3. Электролитом служит насыщенный раствор сернокислого кадмия Сd SO₄4, чтобы раствор был всегда насыщен, над пастой и отрицательным электродом помещаются кристаллыCd SO₄5. Весь стеклянный сосуд заключен в защитный кожух.

При температуре t⁰C (в градусах Цельсия) ЭДС элемента Вестона определяется по формуле

B,(32.10)

От элемента Вестона нельзя потреблять сильный ток, так как он легко поляризуется и после этого ему надо дать восстановиться. Если в течение минуты протекает ток от 0,5 до 10 мкА, то элементу для восстановления требуется отдых от 10 минут до 24 часов, чтобы элемент Вестона имел стандартную ЭДС.

Порядок выполнения работы

Определение ЭДС элементов

1. Собрать схему рис. 32.4.

2. Включить ключ К₂, а ключК₃поставить в положение 1.

3. Произвести компенсацию нормального элемента пять раз и найти пять значенийn_nпоказаний барабана реохорда. Определить среднее значение.

4. Переключить К₃в положение 2, произвести пять раз компенсацию исследуемого элементаЕ_хи найти– среднее значение показаний оборотов барабана.

5. Вычислить ЭДС нормального элемента при комнатной температуре по формуле (32.10). Значение измеряемой ЭДС элемента Е_хнайти по формуле (32.9) подставляя туда средние значенияи.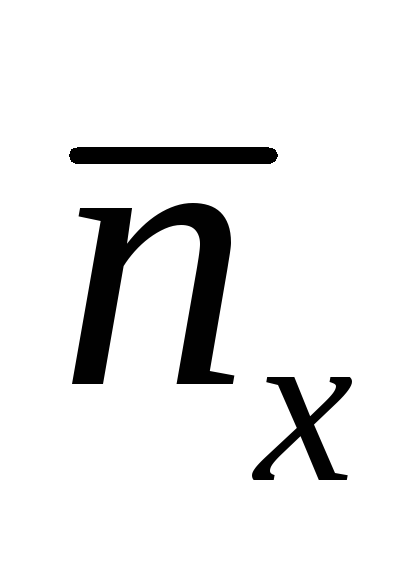

Определение внутреннего сопротивления элемента Е_х

Внутреннее сопротивление элемента определяется следующим образом:

1. На магазине сопротивлений установить определенное сопротивление (по рекомендации преподавателя).

2. Включить ключ К₂, ключК₃поставить в положение 2.

3. Включить ключ и, компенсируя схему пять раз, найти среднее значение показаний барабана реохорда.

4. Внутреннее сопротивление элемента определить по формуле (32.8), которая, учитывая устройство реохорда, приобретает следующий вид:

, (32.11)

где n_х,n_U - обороты реохорда при компенсации ЭДСЕ_хиU.

5. Повторить действия, указанные в пунктах 2 – 4 установив на магазине сопротивлений другие значения сопротивлений.

Формулы для расчета погрешности результатов измерений

Обработка результатов измерений

Доверительные границы погрешностей значений n_n ,n_x,n_Uвычисляют по алгоритму прямых измерений с доверительной вероятностью Р = 0,95. Доверительный интервал для неизвестной величины ЭДС определяют из формулы

.

Внутреннее сопротивление элемента определяют при трех различных значениях R₁. Каждый раз определяютиз пяти измерений, находят среднее значениеи доверительные границы его погрешности по алгоритму прямых измерений.

Содержание отчёта

Отчет должен содержать:

1. Чертеж измерительной схемы.

2. Пять значений величин n_n,n_x,n_U.

3. Расчеты по алгоритму прямых измерений их средних значений и доверительных границ погрешности.

4. Расчет внутреннего сопротивления r₀элементаЕ_хи доверительные границы его погрешности.

Контрольные вопросы

• В чем заключается сущность работы схемы компенсации ЭДС?

• Как определяется внутреннее сопротивление элемента? (Выведите формулу).

• Для каких целей могут быть использованы компенсационные схемы?

Лабораторная работа 33

ОПРЕДЕЛЕНИЕ ЕМКОСТЕЙ КОНДЕНСАТОРОВ И ЭДС ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ ПРИ ПОМОЩИ ГАЛЬВАНОМЕТРА

Задачи работы

1. Градуировка гальванометра.

2. Определение емкости конденсаторов, а также систем конденсаторов.

3. Определение ЭДС гальванических элементов.

Физическое обоснование эксперимента

Если сообщить проводнику электрический заряд, то его потенциал относительно какой-либо точки пространства будет возрастать пропорционально заряду:

,

(33.1)

где q – заряд, φ – потенциал. Коэффициент пропорциональности C называется электрической емкостью (электроемкостью) или просто емкостью проводника. Емкость характеризует способность проводника накапливать электрические заряды. Иными словами, емкостью C называется отношение сообщённого заряда q к возникающему в результате этого потенциалу φ:

,

(33.2)

т. е. численно емкость равна заряду, который необходимо сообщить уединенному проводнику для изменения его потенциала на единицу.

Единицей электроемкости проводников в системе СИ является фарад¹ (устаревшее название – фарада) (Ф, F) – емкость проводника, потенциал которого изменяется на 1 вольт при сообщении проводнику заряда в 1 кулон: 1 Ф = 1 .

Следует иметь в виду, что фарад – очень большая величина (емкость шара с радиусом, равном земному, имеет емкость 7·10^–4 Ф. Чаще применяются дольные единицы: микрофарад (мкФ, F), равный 10^–6 Ф, нанофарад (нФ, nF), равный 10^–9 Ф и пикофарад (пФ, pF), равный 10^–12 Ф.

Емкость определяется геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды (ее диэлектрической проницаемостью) и не зависит от материала проводника. Наличие вблизи проводника других тел изменяет его емкость. Электрическая емкость изолированного проводника мала.

Электрический конденсатор – устройство из нескольких проводников, разделенных слоем диэлектрика.

Простейший конденсатор, состоящий из двух плоских параллельных пластин одинаковой площади (обкладок), разделенных тонким слоем диэлектрика, называется плоским конденсатором (рис. 33.1).

Рис. 33.1. Плоский конденсатор.

Емкость такого конденсатора С = определяется его геометрическими размерами и свойствами диэлектрика. В конденсаторе электрическое поле сосредоточено в основном между его обкладками, поэтому емкость конденсатора практически не зависит от окружающих тел и может достигать больших величин при малых размерах конденсатора. Если на единице поверхности обкладок имеется заряд σ и диэлектриком является вакуум, то полное напряжение между обкладками равно:

,

(33.3)

где U – напряжение между пластинами, d – расстояние между пластинами. Если площадь каждой пластины равна S, то полный заряд пластины есть q = σS. Поэтому:

.

(33.4)

Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью , заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость будет в  раз больше:

.

(33.5)

Электрические конденсаторы часто включаются группами (в виде батарей). При присоединении нескольких конденсаторов друг к другу различают параллельное (рис. 33.2) и последовательное (рис. 33.3) их соединения.

Рис. 33.2. Параллельное соединение конденсаторов: C_ОБЩ = С₁ + С₂ + C₃ + … + С_n.

При параллельном соединении конденсаторов (рис. 33.2) одна из пластин каждого конденсатора имеет один и тот же потенциал φ₁, а другая φ₂. На пластинах каждого конденсатора находится заряд q_i (i = 1, 2, 3, ..., n), так что суммарный заряд всех конденсаторов равняется:

.

(33.6)

Отсюда следует:

, .

(33.7)

Рис. 33.3. Последовательное соединение конденсаторов: .

При последовательном соединении конденсаторов (рис. 33.3) под влиянием приложенной разности потенциалов их пластины электризуются так, что на них появляются равные, но противоположные по знаку заряды q. Разности потенциалов пластин каждого конденсатора суммируются (пусть n = 3):

.

(33.8)

Следовательно:

.

(33.9)

Метод исследования и описание установки

В данной работе в качестве измерительного прибора используется баллистический гальванометр. Баллистический гальванометр применяется для измерений количества электричества и представляет собой магнитоэлектрический гальванометр с искусственно увеличенным моментом инерции подвижного индикатора (период собственных колебаний T₀≥ 15 c), включаемый последовательно в цепь, по которой протекает импульсный ток. Если длительность импульса тока много меньше T0, то первое наибольшее отклонение индикатораl_m(баллистический отброс) после протекания тока пропорционально количеству электричестваq, протекающего через рамку баллистического гальванометра:

q =КГ lm,

(33.10)

где K_Г – баллистическая постоянная по заряду или просто постоянная гальванометра, l_m – баллистический отброс.

Баллистическая чувствительность по заряду (чувствительность к протекающему через баллистический гальванометр заряду) и обратная ей величина (баллистическая постоянная K_Г) зависят от сопротивления внешней электрической цепи, на которую замкнут баллистический гальванометр во время измерений. Поэтому баллистический гальванометр градуируют при том же внешнем сопротивлении, при котором будут выполняться измерения.

Если известна баллистическая постоянная гальванометра, то по баллистическому отбросу можно определить заряд q, прошедший через гальванометр. В работе через гальванометр пропускается заряд конденсатора С (Рис.33.4), который будет определяться емкостьюСвключенного в схему конденсатора и электродвижущей силой элемента питанияЕ. В соответствии с формулой 33.4q = C E. Таким образом, если известна ЭДС элемента, то можно определить емкость и наоборот.

Работа выполняется на одной из трех установок (электрическая схема, состоящая из гальванометра (обычно М195/3 или М197/2), нормального элемента Вестона (Ε₀= 1,0183 В), магазина емкости (обычно Р5025 или Р523), двух неизвестных конденсаторов и переключателя), а также двух гальванических элементов с неизвестными ЭДС (в состав установки не входят – получите у лаборанта).

В качестве С в данную схему может быть включен либо магазин емкости либо исследуемые конденсаторы, в качестве Е либо нормальный элемент либо исследуемый элемент.

Рис. 33.4. Рабочая схема.

Порядок выполнения работы