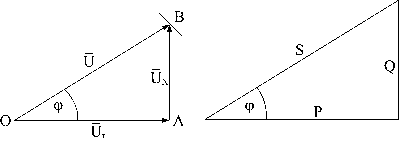Санкт-петербургский государственный университет Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета сПбГу

Часть V

ЭЛЕКТРИЧЕСТВО

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

САНКТ-ПЕТЕРБУРГ•2004

ББК 22.33

Утверждено на заседании Кафедры общей физики 2 физического факультета СПбГУ

Ответственные редакторы: В.И. Коротков, Е.П. Зароченцева

Авторы: А.В. Бармасов, С.О. Высоцкая, А.Е. Грищенко, Л.В. Густова, Е.П. Зароченцева, Т.Н. Компаниец, В.И. Коротков, Н.А. Малешина,

В.А. Черенковский. Составитель: А.В. Бармасов

Рецензент: докт.физ.-мат. наук., проф. В.А. Соловьев (СПбГУ)

Печатается по постановлению Редакционно-издательского совета С.-Петербургского государственного университета

Б24	Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета СПбГУ. Часть V: Электричество. Переменный электрический ток / А.В. Бармасов, С.О. Высоцкая, А.Е. Грищенко и др.; Под ред. В.И. Короткова, Е.П. Зароченцевой; СПб., 2004.  111 с.

Данное пособие содержит описания лабораторных работ по разделу «Электричество. Переменный электрический ток» курса общей физики и представляет собой существенно переработанное и дополненное переиздание учебного пособия «Электричество (переменный ток). Ч. 5 / Под ред. В.Е. Холмогорова и Ю.Г. Шишкина.» (Л.: Изд-во ЛГУ, 1990. 83 с.). Каждая лабораторная работа рассчитана на 4 академических часа. Студент допускается к выполнению лабораторной работы после самостоятельного изучения необходимой теории, ознакомления с порядком выполнения основных операций и сдачи зачёта по технике безопасности. Предназначено для студентов факультетов: биолого-почвенного, географии и геоэкологии, геологического, медицинского, физического (вечернее отделение), химического и др.

ББК 22.33

 А.В. Бармасов,

С.О. Высоцкая,

А.Е. Грищенко и др., 2004.

 Санкт-Петербургский

государственный

университет, 2004.

СОДЕРЖАНИЕ

1. Электроизмерительные приборы ...............................................	6
Классификация электроизмерительных приборов ...................	6
Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора ............................	9
Масштабные измерительные преобразователи (МИП) ...........	12
Ваттметр .......................................................................................	16
2. Переменный электрический ток ................................................	21
Сопротивление R .........................................................................	21
Емкость С .....................................................................................	22
Индуктивность L ..........................................................................	23
3. Понятие о векторных диаграммах .............................................	26
Последовательное соединение элементов .................................	27
Параллельное соединение элементов ........................................	30
4. Мощность переменного тока .......................................................	32
5. Мостовой метод измерения ..........................................................	36
Мост Уитстона .............................................................................	36
Мосты переменного тока ............................................................	37
Лабораторная работа 42 Проверка закона ома для переменного тока .....................................	40
Лабораторная работа 43 Исследование цепей переменного тока с активными и индуктивными сопротивлениями ......................................................................	48
Лабораторная работа 44 Измерение емкостей конденсаторов с помощью моста переменного тока ...............................................................................................	55
Лабораторная работа 45 Измерение индуктивностей катушек с помощью моста переменного тока ...............................................................................................	58
Лабораторная работа 46 Изучение работы трансформатора .....................................................	64
Лабораторная работа 47 Резонанс напряжений в цепях переменного тока .............................	73
Лабораторная работа 48 Определение коэффициента мощности однофазного переменного тока и построение треугольников мощностей ..................................	81
Лабораторная работа 50 Изучение свойств ферромагнитных веществ с помощью электронного осциллографа .......................................................................	89
Приложения ........................................................................................	98
Аналоговые электроизмерительные приборы ..........................	98
Краткая характеристика электроизмерительных приборов наиболее распространенных систем ..........................................	101
Измерительные трансформаторы тока и напряжения .............	102
Построение векторных диаграмм ..............................................	103
Литература ..........................................................................................	111

ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

Измерение – это нахождение опытным путем с оцененной точностью значения заранее выбранной физической величины путем сравнения ее с эталонной величиной. Электрические измерения осуществляются с помощью электроизмерительных приборов (ЭИП).

Объектами электрических измерений могут быть как электрические и магнитные величины, так и неэлектрические величины (такие, например, как давление, скорость, температура). Для того чтобы измерить неэлектрическую величину с помощью электроизмерительных приборов, ее надо преобразовать в зависящую от нее электрическую величину. Устройства для измерения неэлектрических величин должны содержать преобразователь, соединительные провода и электроизмерительный прибор, шкала которого проградуирована в единицах измеряемой величины.

В качестве одного из наиболее простых примеров можно привести измерение температуры с помощью термопары. Величина электродвижущей силы (эдс) термопары зависит от разности температур между горячим и холодным спаями, т.е. термопара является в данном случае преобразователем. С помощью проводов к ней подключается милливольтметр, измеряющий эдс термопары (термоЭДС). В этом случае шкалу милливольтметра можно проградуировать в единицах температуры.

Классификация электроизмерительных приборов

ЭИП можно классифицировать по различным признакам:

По характеру снимаемых показаний измеряемой величины.

Показывающие ЭИП. Это приборы, предварительно отградуированные и позволяющие производить по шкале отсчет численного значения измеряемой величины. С помощью таких приборов можно сразу получить значение измеряемой величины.

Регистрирующие ЭИП. Эти приборы допускают считывание и регистрацию или только регистрацию показаний. К таким приборам относятся самопишущие приборы, дающие запись показаний в виде диаграммы, печатающие приборы, выводящие показания в цифровой форме, а также осциллографы. Для получения значений измеряемой величины такие приборы требуют специальной градуировки.

По способу преобразования измеряемой величины и способу считывания показаний.

Аналоговые ЭИП. В этих приборах показания являются непрерывными функциями изменений измеряемых величин.

Примером аналогового прибора может служить стрелочный амперметр (рис. 1).

Рис. 1.

При увеличении тока стрелка амперметра смещается плавно. Тем не менее плавность изменения показаний не означает, что величина тока может быть измерена с любой точностью (см. ниже).

Цифровые приборы. В таких приборах непрерывно изменяющийся измеряемый параметр преобразуется в дискретный параметр (число), которое отображается на его отсчетном устройстве – панели цифровой индикации (рис. 2).

Рис. 2.

При плавном изменении тока показания прибора изменяются скачками.

Приборы сравнения. Это приборы, предназначенные для непосредственного сравнения измеряемой величины с величиной, значение которой известно. К таким приборам относятся, например, мосты, потенциометры, компенсаторы напряжения и тока.

Простейшим примером схемы сравнения может служить компенсатор напряжения. Принцип работы компенсатора напряжения показан на рис. 3.

ЭДС источников равны, когда показания гальванометра равно нулю. Основное достоинство такого способа измерения состоит в том, что в этом случае не происходит отбора тока от источника. Этот способ удобен для измерения ЭДС источников с большим внутренним сопротивлением.

Рис. 3.

Особенно хорошо видны преимущества методов сравнения при измерении сопротивлений. Можно определить сопротивление, воспользовавшись амперметром и вольтметром (R = U/I). Такой способ (способ амперметра и вольтметра) является наиболее простым, но наименее точным из-за присущей ему систематической ошибки.

Два варианта включения измерительных приборов показаны на рис. 4. На рис. 4,а приведена схема «правильная по напряжению», но амперметр показывает сумму токов, текущих через вольтметр и нагрузку. На рис. 4,б – схема «правильная по току», но вольтметр показывает сумму падений напряжения на амперметре и нагрузке.

Рис. 4.

Широкое применение для измерения сопротивлений получили мосты, питаемые постоянным током, так как их уравновешивание несложно и подбор подходящего гальванометра не составляет особого труда.

Примером такой схемы сравнения может служить четырехплечевой мост постоянного тока, применяемый для измерения сопротивлений (рис. 5).

В одно из плеч моста включен неизвестный резистор R_X. При измерении сопротивления таким методом, неизвестное сопротивление сравнивается с известными сопротивлениями моста, а включенный в одну из диагоналей моста гальванометр Г служит индикатором отсутствия тока.

Рис. 5.

Точность измерения в данном случае определяется точностью значений известных сопротивлений и чувствительностью гальванометра.

Мосты переменного тока применяются, в основном, для измерения индуктивностей и емкостей.

Более подробно – см. «Мостовой метод измерения».

Определение погрешности измерения на электроизмерительных приборах. Класс точности прибора

Следует помнить, что никакое измерение, т.е. сравнение с эталонной величиной, не может быть выполнено абсолютно точно. Результат измерения всегда содержит некоторую ошибку. Кроме того, надо учесть, что измерение проводится не путем сравнения с самим эталоном, а с помощью измерительного прибора (который при поверке был сравнен с эталоном). Очевидно, что, измеряя с помощью этого измерительного прибора, мы не можем сделать ошибки меньшей, чем та, которая определяется погрешностью измерительного устройства.

Разность между показаниями прибора и действительным значением измеряемой величины называется абсолютной погрешностью А.

А = АИЗМ – АДЕЙСТ .

(1)

Отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в процентах, называется относительной погрешностью:

.

(2)

Приведенные определения относительной и абсолютной погрешности не дают возможности узнать их величину, так как действительное значение измеряемой величины нам неизвестно. Определить величины погрешностей при электрических измерениях становится возможным, если известен класс точности прибора (_{КЛ Т}). Он дает предельную абсолютную погрешность, выраженную в процентах от номинального показания прибора (максимального при данном пределе измерения) А_НОМ:

КЛ Т = .

(3)

Класс точности указан на шкале прибора (рис. 6).

Зная класс точности прибора, можно легко определить абсолютную погрешность измерения А:

А = .

(4)

Например, для катушки сопротивления в 1000 Ом класса точности 0,05 абсолютная погрешность:

А = = 0,5 (Ом).

Относительную погрешность также можно вычислить через класс точности прибора. По определению относительная погрешность:

.

(5)

Учитывая, что действительное значение измеряемой величины А_ДЕЙСТ и показания прибора А_ИЗМ примерно равны (А_ДЕЙСТ  А_ИЗМ), и, используя формулу (4), получаем:

.

(6)

Видно, что относительная погрешность измерений будет тем меньше, чем ближе снимаемые показания к номинальному значению для данного прибора, т.е. к концу шкалы. Следовательно, при работе с многопредельными ЭИП нужно так выбирать предел измерения прибора, чтобы показания считывались со второй половины шкалы. Следует помнить, что номинальное значение многопредельного ЭИП определяется положением, в котором стоит переключатель пределов при данном измерении.

При работе с многопредельными приборами нужно внимательно рассчитывать цену одного деления шкалы Ц_Д. Под делением следует понимать не разность между штрихами, а разность между ними в соответствии с оцифровкой шкалы. Цена деления равномерной шкалы равна отношению номинального значения показания прибора (предела измерения) к общему числу делений N на шкале прибора: Ц_Д = . Численное значение измеряемой величины А_ИЗМ равно цене деления Ц_Д, умноженной на измеренное число делений N_ИЗМ по шкале:

АИЗМ = ЦД·NИЗМ.

(7)

Рассмотрим примеры определения погрешностей для многопредельных ЭИП.

Пример 1.
Переключатель пределов измерения	→		← ←	Шкала прибора Класс точности КЛ Т (0,5)
Рис. 6.

На рис. 6 изображен многопредельный вольтметр. Вычислить абсолютную и относительную погрешности определения напряжения. Класс точности вольтметра 0,5.

Номинальное значение напряжения 300 В (определяется положением переключателя пределов напряжения).

Цена деления данного предела измерения Ц_Д == 2 В/дел.

Измеренное значение напряжения U_ИЗМ = 2 В/дел.·75 дел. = 150 В.

Абсолютная погрешность измерения U = = 1,5 (В).

Относительная погрешность измерения ₀ = = 1,0%.

Пример 2

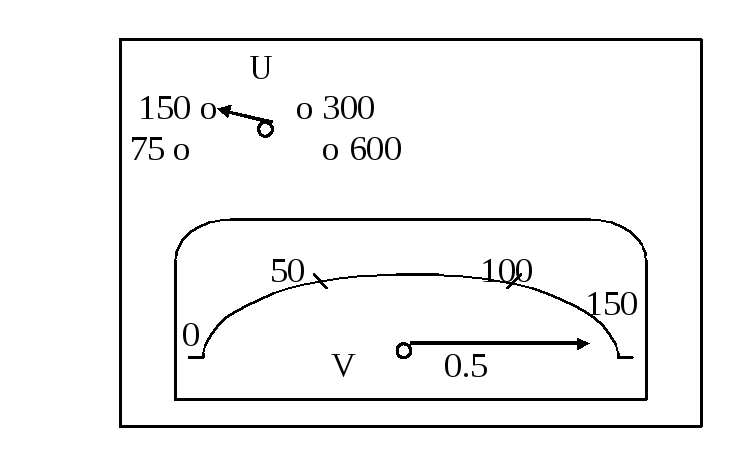
Рис. 7.

На рис. 7 изображен тот же многопредельный вольтметр при другом положении переключателя пределов измерений. Вычислить абсолютную и относительную погрешности определения напряжения.

Номинальное значение напряжения 150 В.

Цена деления данного предела измерения Ц_Д = 150 В / 150 дел. = 1 В/дел.

Измеренное значение напряжения U_ИЗМ = 1 В/дел.×150 дел. = 150 В.

Абсолютная погрешность измерения U = = 0,75 (В).

Относительная погрешность измерения ₀ = = 0,5%.

Таким образом, выбор наиболее подходящего предела измерения приводит к уменьшению как абсолютной, так и относительной погрешности.

Масштабные измерительные преобразователи (МИП)

При необходимости измерения токов и напряжений, превышающих верхний предел измерения используемого прибора, используются МИПы.

Для приборов постоянного тока в качестве МИП используются шунты и добавочные сопротивления. Для приборов переменного тока – добавочные резисторы (для напряжений до 30 кВ и частот от 10 Гц до 20 кГц) и измерительные трансформаторы тока и напряжения.

Расчет шунта к амперметру

При измерении тока амперметр включается последовательно с нагрузкой. Если амперметром требуется измерить ток, превышающий верхний предел измерения, то параллельно амперметру включается шунт с сопротивлением R_Ш (рис. 8). Шунт представляет собой толстую константановую или манганиновую пластину. Применение этих сплавов для изготовления шунтов связано с тем, что их сопротивление слабо зависит от температуры.

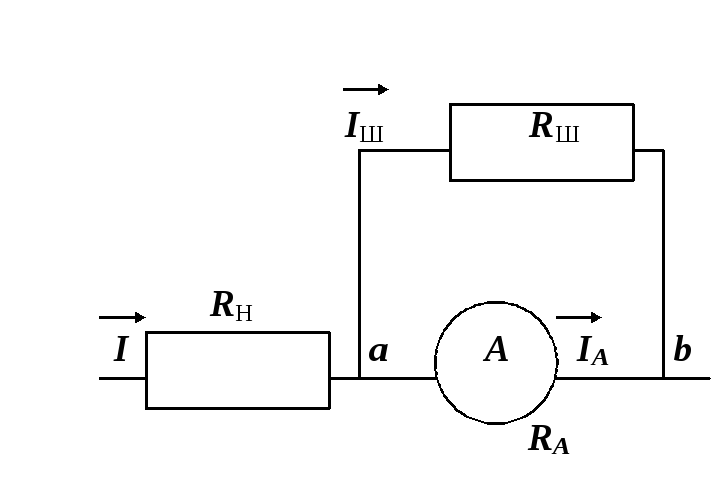
Рис. 8.

На рис. 8 показана схема подключения шунта R_Ш к амперметру. R_А – внутреннее сопротивление амперметра, которое мало по сравнению с сопротивлением нагрузки R_Н для того, чтобы включение амперметра последовательно с нагрузкой не приводило к существенным изменениям тока в цепи нагрузки. I – ток через сопротивление нагрузки R_Н; I_Ш – ток через шунт с сопротивлением R_Ш; I_А – ток через амперметр с сопротивлением R_А.

По первому правилу Кирхгофа алгебраическая сумма токов в узле равна нулю:

I = I_А + I_Ш

и, следовательно,

I_Ш = I – I_А.

Падение напряжения между точками а и b:

U_аb = I_А·R_А = I_Ш·R_Ш.

Таким образом, для того, чтобы с помощью данного амперметра измерить ток I, сопротивление шунта должно быть

RШ = ,

(8)

где I/I_A = n – коэффициент шунтирования, показывающий, во сколько раз расширяется предел измерения амперметра при подключении шунта.

Фактический ток в цепи определяется произведением показаний прибора и множителя n.

Рис. 9.

Реальный шунт (рис. 9) должен иметь четыре контакта: к двум из них подключается прибор, а к двум другим – соединительные провода электрической цепи.

Пример 3.

Рассчитать шунт к миллиамперметру на 10 mА с внутренним сопротивлением 500 Ом, если надо измерить ток 10 А.

Воспользуемся формулой (8):

Расчет добавочного сопротивления к вольтметру

Для измерения напряжения вольтметр включается параллельно с нагрузкой. Если вольтметром требуется измерить напряжение, превышающее верхний предел измерения, то последовательно вольтметру включают добавочное сопротивление R_Д.

Рис. 10.

На рис. 10 показана схема подключения добавочного сопротивления R_Д к вольтметру. R_V – внутреннее сопротивление вольтметра. Оно должно быть большим по сравнению с сопротивлением нагрузки R_Н для того, чтобы включение вольтметра параллельно нагрузке не приводило к существенным изменениям напряжения на нагрузке. U_ИЗМ – измеряемое напряжение; U_НОМ – предел измерения вольтметра.

Ток, текущий через вольтметр:

,

следовательно, добавочное сопротивление должно быть

.

(9)

Пример 4

Рассчитать добавочное сопротивление к вольтметру на 100 В для измерения напряжения 300 В. Внутреннее сопротивление вольтметра R_V = 3000 Ом.

.

Добавочные сопротивления могут служить и для преобразования рода измеряемой величины (напряжения в ток и наоборот). Рассмотрим, как измерить напряжение с помощью амперметра. Для этого последовательно с амперметром включается большое сопротивление R_Д (рис. 11).

Рис. 11.

Неизвестное напряжение U_X = I_А·(R_Д + R_А), где R_А – внутреннее сопротивление амперметра. Если величины внутреннего и добавочного сопротивлений известны, то, измеряя ток с помощью амперметра, легко вычислить искомое напряжение.

Ваттметр

Для измерения мощности в цепи постоянного тока не требуется специального прибора. Мощность в цепи постоянного тока может быть определена, если известны показания вольтметра и амперметра, т.е. напряжение и ток, и вычислена простым перемножением этих величин:

P = U·I.

В цепи переменного тока мощность зависит не только от величин напряжения и тока, но и от сдвига фаз между ними (подробнее см. раздел «Мощность переменного тока»):

P = U·I·cosφ.

Поэтому для измерения мощности в цепях переменного тока необходим специальный прибор – ваттметр.

Ваттметр электродинамической системы имеет две катушки (сопротивление катушек малó): неподвижную («токовую») К₁, включаемую последовательно нагрузке, и подвижную («вольтовую») К₂, включаемую параллельно нагрузке. В цепь подвижной катушки включается добавочное сопротивление R_Д. Сопротивление R_Д должно быть большим по величине для того, чтобы ток через цепь, содержащую это сопротивление, был незначительным по сравнению с током нагрузки. То есть сопротивление «вольтовой» цепи должно быть большим, как у всякого вольтметра.

Рис. 12.

Схема включения ваттметра (рис. 12): К₁ – неподвижная («токовая») катушка («цепь тока»); К₂ – подвижная («вольтовая») катушка («цепь напряжения»); R_H – сопротивление нагрузки; R_Д – добавочное сопротивление в цепи подвижной катушки.

Как видно из схемы, через неподвижную катушку проходит тот же ток, что и через сопротивление нагрузки (I₁(t)), а через подвижную протекает ток, пропорциональный напряжению на нагрузке. Таким образом, мгновенное значение тока неподвижной катушки равно току нагрузки, а ток подвижной катушки пропорционален напряжению на нагрузке и должен совпадать с ним по фазе. Чтобы ток совпадал по фазе с напряжением, добавочное сопротивление R_Д должно быть безиндуктивным, т.е. чисто активным сопротивлением. Величина этого сопротивления должна быть много больше индуктивного сопротивления катушки К₂. В таком случае можно считать все сопротивление цепи напряжения активным и ток I₂(t) в подвижной катушке будет равен

,

(10)

где U₀ – амплитуда напряжения на нагрузке,  – частота переменного тока,  – сдвиг фаз между током и напряжением на нагрузке. Как уже было отмечено выше, сдвиг фаз между током в подвижной и неподвижной катушках будет равен сдвигу фаз между током и напряжением на нагрузочном сопротивлении только в том случае, когда сопротивление «вольтовой» цепи ваттметра можно считать активным.

Согласно закону Ампера, сила, действующая на элемент тока со стороны другого элемента тока, пропорциональна величине каждого из элементов тока. Следовательно, мгновенный вращающий момент M(t), действующий на подвижную катушку, пропорционален произведению токов в подвижной и неподвижной катушках:

M(t) = с·I1(t)·I2(t),

(11)

где с – константа пропорциональности.

Подставляя в формулу (11) выражение для тока в подвижной катушке (10), получаем:

.

(12)

Усредняя M(t) за период Т, находим:

.

(13)

Таким образом, вращающий момент, действующий на подвижную катушку, и, следовательно, угол ее поворота, пропорционален средней мощности в цепи переменного тока.

Реальный ваттметр имеет 4 клеммы, на принципиальной схеме они обозначены буквами A, B, C и D. При включении ваттметра в цепь переменного тока, на вращающий момент не влияет одновременное изменение направления тока в обеих катушках, но если поменять направление тока только в одной катушке, то направление вращающего момента изменится на 180°. Для предотвращения неправильного включения ваттметра клеммы, соответствующие относительным «началам» каждой катушки, отмечены звездочкой (). Эти клеммы называют генераторными. Стрéлка ваттметра отклоняется в нужную сторону, если обе эти клеммы присоединены к одному полюсу источника. Обычно эти клеммы уже соединены вместе проводом (A и B). Клеммы A и D подсоединяют к источнику напряжения, а нагрузку включают между клеммами C и D.

Многопредельные ваттметры имеют раздельные переключатели напряжения и тока для «вольтовой» и «токовой» обмоток. Изменение пределов измерения по току осуществляется путем последовательного или параллельного включения двух половин неподвижной катушки, а по напряжению – включением добавочных сопротивлений в цепь подвижной катушки. Для таких приборов предел измерения по мощности в ваттах равен произведению пределов измерения по току в амперах и по напряжению в вольтах. В общем случае предельная нагрузка ваттметра и конечное значение шкалы у ваттметра не совпадают в отличие от большинства других приборов. При чисто реактивной нагрузке сдвиг фаз между током и напряжением  = 90°. В этом случае ваттметр легко вывести из строя, так как при любой силе тока, протекающего через ваттметр, его показание будет всегда равно нулю (cоs = 0). Обычные ваттметры рассчитаны на измерения, при которых соs > 0,8. Исключение составляют ваттметры, специально предназначенные для малых значений соs (малокосинусные ваттметры).

Рис. 13.

На рис. 13 изображена верхняя панель многопредельного ваттметра класса точности 1,5. При данном положении переключателей предельное (номинальное) значение измеряемой мощности будет P_НОМ = 300 В · 2 А = 600 Вт. Варьируя положение переключателей, предел измерения данного ваттметра можно изменять от 75 Вт до 1800 Вт.

При работе с многопредельными ваттметрами нужно внимательно рассчитывать цену одного деления шкалы Ц_Д. Цена деления шкалы равна отношению номинального значения мощности (предел измерения ваттметра) к общему числу делений N на шкале прибора: Ц_Д = P_НОМ/N. Для прибора, изображенного на рис. 13, цена деления Ц_Д = 600 Вт/150 дел. = 4 Вт/дел.

Численное значение измеряемой мощности P_ИЗМ равно цене деления, умноженной на число делений по шкале (в данном случае ваттметр показывает 100 делений): P_ИЗМ = 4 Вт/дел.  100 дел. = 400 Вт.

Так же, как и для других электроизмерительных приборов, величина как абсолютной, так и относительной погрешности, зависит от выбранного предела измерений.

При положении переключателей, изображенном на рис. 13, абсолютная погрешность P измеренной мощности будет, согласно формуле (4):

9 (Вт),

а относительная погрешность ₀ измерения мощности, согласно (6):

.

Если проводить измерения при другом положении переключателей (рис. 14), то ту же самую величину мощности (400 Вт) можно измерить тем же ваттметром с меньшей погрешностью.

Рис. 14.

Предел измерения ваттметра (номинальное значение мощности) в данном случае будет: P_НОМ = 150 В  3 А = 450 Вт,

цена деления: Ц_Д = 450 Вт / 150 дел. = 3 Вт/дел.,

абсолютная погрешность: P = (_КЛ.Т.·P_НОМ)/100 = (1,5·450)/100 = 6,75 (Вт),

относительная погрешность:

.

Таким образом, выбор наиболее подходящего предела измерения приводит к уменьшению как абсолютной, так и относительной погрешности.

Читайте также раздел «Приложения».

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Переменный электрический ток – это электрический ток, изменяющийся во времени. К переменному току относят различные виды импульсных, пульсирующих периодических и квазипериодических токов. В технике под переменным током обычно подразумевают периодические токи переменного направления. Чаще всего применяется переменный ток, сила которого меняется во времени по гармоническому закону (гармонический, или синусоидальный переменный ток).

Рассмотрим процессы, происходящие в цепях, по которым протекает переменный гармонический ток. Предположим, что режим прохождения тока установился, т.е. собственные колебания в цепи затухли, и физические процессы в цепи представляют собой вынужденные колебания. Такие предположения позволяют избежать математических трудностей, связанных с решением дифференциальных уравнений, и существенно упростить анализ процессов происходящих в цепях переменного тока.

Рассмотрим частные случаи, когда переменное напряжение U(t) = U₀·cost подается или на сопротивление R, или на емкость C, или на индуктивность L.

Сопротивление R

Если в качестве нагрузки выступает активное сопротивление R, то ток в цепи определяется соотношением:

Видно, что в такой цепи колебание тока происходит синфазно с колебаниями напряжения, без сдвига по фазе между напряжением и током. Амплитудные значения тока и напряжения связаны соотношением

.

(14)

Емкость С

Если цепь состоит только из емкости C, то изменение тока со временем определяется скоростью изменения заряда конденсатора I = dq/dt. Так как q = C·U(t), то

,

(15)

где I₀ = ·C·U_0.

То есть ток в цепи, состоящей только из емкости, изменяется со временем, так же как и напряжение, по синусоиде, но опережает по фазе напряжение на . Временнáя зависимость напряжения и силы тока в такой цепи представлена на рис. 15.

Рис. 15.

Кроме того, видно, что если ввести понятие емкостного сопротивления , то амплитудные значения напряжения U₀ и тока I₀ связаны законом Ома

.

(16)

Сдвиг по фазе можно объяснить следующим образом. Возьмем заряженный конденсатор, который начинает разряжаться. Это значит, что напряжение начинает убывать, а ток - увеличиваться по абсолютной величине. Когда напряжение на обкладках конденсатора окажется равным нулю, ток достигнет максимума. Далее происходит изменение знака напряжения, что соответствует перезарядке конденсатора. После чего напряжение по абсолютной величине начинает увеличиваться, а сила тока уменьшаться. Описанные процессы иллюстрируют возникновение сдвига по фазе между напряжением и силой тока на .

Индуктивность L

Пусть через катушку (соленоид), характеризующуюся постоянной самоиндукции (или индуктивностью) L, проходит переменный ток I(t) = I₀·cost.

По закону электромагнитной индукции (Фарадея - Ленца) в любом замкнутом контуре при изменении магнитного потока через поверхность (площадь), ограниченную этим контуром, возникает ЭДС индукции E, пропорциональная скорости изменения магнитного потока

,

где Φ – магнитный поток, k – коэффициент (в системе СИ k = 1). Знак «минус» означает, что направление индукционного тока таково, что создаваемое им магнитное поле препятствует изменению первичного магнитного потока.

Частным случаем проявления этого эффекта является возникновение самоиндукции при любых изменениях тока в цепи. В простейшем случае (при отсутствии ферромагнетиков) Φ = L·I, где L – индуктивность проводника, зависящая от его размеров, формы и свойств среды. Изменения тока вызывают изменения создаваемого им магнитного потока, что в свою очередь приводит к появлению ЭДС самоиндукции E, равной

.

ЭДС самоиндукции в цепи, состоящей из соленоида, в каждый момент времени компенсируется напряжением U, подаваемым на индуктивность L. То есть

.

(17)

Тогда

,

(18)

где U₀ = ·L·I₀.

Формула (18) показывает, что напряжение в цепи опережает ток на .

Если ввести понятие индуктивного сопротивления X_L = ·L, то амплитудные значения напряжения и силы тока можно связать законом Ома:

.

(19)

Согласно (14), (16) и (19) закон Ома справедлив для амплитудных значений напряжения и тока.

Закон Ома для мгновенных значений переменного тока можно использовать только для случая активного сопротивления R.

Величину переменного тока можно охарактеризовать амплитудными значениями тока или напряжения. Это целесообразно делать, например, при подборе изоляции каких-либо электротехнических деталей, так как «пробои» возникают именно в моменты, когда переменное напряжение достигает максимальных значений.

На практике обычно вводят понятие эффективных (действующих) значения величин силы тока I_эфф и напряжения U_эфф, чтобы формула для поглощаемой (отдаваемой сопротивлению) мощности имела тот же вид, что и для цепей постоянного тока¹:

,	(20)
.	(21)

Тогда

P = Iэфф·Uэфф·cosφ.

(22)

Легко показать, что эффективное значение переменного тока I_эфф равно такому значению постоянного тока I, который выделяет на

сопротивлении R за одно и то же время t столько же тепла Q, что и данный переменный ток.

В обозначениях переменного напряжения U, и силы тока I, под U и I обычно понимают эффективные значения тока и напряжения. Напряжение сети переменного тока «220В» является именно эффективным напряжением, и именно эффективные значения тока и напряжения измеряют амперметры и вольтметры.

ПОНЯТИЕ О ВЕКТОРНЫХ ДИАГРАММАХ

Реальные электрические цепи представляют какие-либо комбинации простейших элементов R, C и L.

Чтобы определить связь между током и напряжением в цепи, включающей несколько различных элементов, необходимо уметь складывать гармонические колебания одной частоты, но с разными амплитудами и фазами. Такую задачу аналитически бывает решить сложно, но существует графический метод, позволяющий сделать это достаточно просто и наглядно, – это метод векторных диаграмм.

Д анный метод основан на том, что изменяющуюся по гармоническому закону величину, например, a(t) = A₀·sin(t + ) (или a(t) = A₀·cos(t + )), можно представить как проекцию на ось ординат (или ось абсцисс) радиус-вектора, вращающегося против часовой стрелки с угловой скоростью  (рис. 16) – a₁ = A₀·sinωt₁, a₂ = A₀·sinωt₂.

Рис. 16.

Длина такого вектора должна быть равна амплитуде колебаний, т.е. в данном случае равна A₀¹. Начальное его положение при t = 0 должно составлять с осью X угол  ( – начальная фаза колебаний). Совокупность нескольких векторов, изображающих гармонически изменяющиеся величины одной и той же частоты называется векторной диаграммой.

Взаимная ориентация векторов сохраняется в любой момент времени, если складываемые колебания имеют одну и ту же частоту, поэтому для построения векторных диаграмм токов и напряжений достаточно указать их фазовые углы в момент t = 0.

П ри построении векторных диаграмм используется математическая теорема, согласно которой проекция геометрической суммы векторов на любую ось равна алгебраической сумме их проекций на ту же ось. Поэтому задача сложения выражений типа U(t) = U₀·sin(t + ) сводится к простой графической задаче сложения векторов (рис. 17 – u₁ = U₁₀·sinφ₁, u₂ = U₂₀·sinφ₂, u = u₁ + u₂ = U₀·sinφ).¹

Рис. 17.

Последовательное соединение элементов

Рассмотрим последовательное соединение емкости, индуктивности и активного сопротивления, к которым приложено переменное напряжение U(t) = U₀·cost (рис. 18).

В случае последовательного соединения в каждый момент времени сила тока во всех участках цепи одна и та же, а сумма мгновенных падений напряжения на элементах равна значению приложенного к цепи напряжения в тот же момент времени:

U(t) = UR(t) + UC(t) + UL(t).	(23)

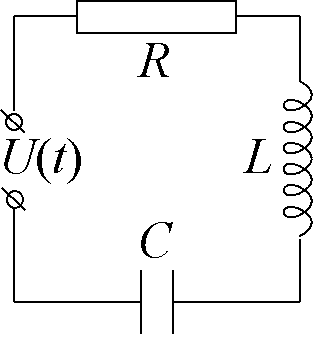
Рис. 18.

Представим соотношение (23) в виде векторной диаграммы и с ее помощью найдем связь между амплитудными и мгновенными значениями тока и напряжения в рассматриваемой цепи.

а	б
Рис. 19.

U_R совпадает по фазе с током, значит, вектор U_0R направлен так же как вектор I₀, U_C отстает от тока на /2, значит, U_0C развернут на /2 «назад» относительно U_0R, а U_0L, соответственно «вперед» (рис. 19,а). Поскольку эти векторы вращаются с одной частотой  против часовой стрелки, то их взаимное расположение друг относительно друга не изменяется, и найти суммарное напряжение U₀ можно в любой момент времени (рис. 19,б).

Из рис. 19,б видно, что

U02 = U0R2 + (U0L – U0C)2,	(24)
,	(25)

где  – угол между векторами I₀ и U₀.

Воспользовавшись формулами (14), (16) и (19) можно вместо (24) и (25) записать:

,	(26)
.	(27)

Величина называется полным сопротивлением цепи или импедансом, а формула (26) - обобщенным законом Ома. По аналогии с треугольником, образуемым амплитудными значениями падений напряжения, можно построить треугольник сопротивлений (рис. 20) Графически полное сопротивление будет представлять собой гипотенузу прямоугольного треугольника. Один катет такого треугольника равен R – его называют активным сопротивлением. Другой катет равен (·L – ), эту составляющую полного сопротивления называют реактивным сопротивлением и обычно обозначают X:

X = XL – XC = ·L – .

(28)

Рис. 20.

При условии ·L = полное сопротивление цепи минимально и равно активному сопротивлению R₀. Формула (26) показывает, что величина переменного тока в цепи существенно зависит от его частоты. При частоте  = амплитудные значения тока принимают максимальные значения I_0max = U₀/R. Такое явление называют резонансом напряжений, а частоту  = называют резонансной частотой электрической цепи. Величина тока при резонансе получается тем больше, чем меньше активное сопротивление цепи.

Параллельное соединение элементов

Рассмотрим цепь переменного тока, содержащую параллельно соединенные элементы R, L и C (рис. 21).

Рис. 21.

Пусть U(t) = U₀·cost. Напряжение на всех элементах цепи одинаково и равно U(t). Мгновенное значение тока в неразветвленной части цепи I(t) равно сумме токов в параллельных участках:

I(t) = IR(t) + IC (t) + IL(t).

(29)

В этом случае удобно строить векторную диаграмму для токов.

С учетом, что ток через сопротивление находится в фазе с приложенным напряжением, ток через участок, содержащий С, опережает напряжение на , а через участок, содержащий L, отстает от напряжения на , векторную диаграмму можно изобразить следующим образом (рис. 22).

Рис. 22.

Из диаграммы видно, что

I0 = .

(30)

При этом

I0R·R = = I0L··L = U0.

(31)

Воспользовавшись векторной диаграммой и формулой (31), нетрудно получить выражения для амплитуды тока через неразветвленную часть цепи и для сдвига по фазе между приложенным напряжением и током

,	(32)
.	(33)

Из векторной диаграммы следуют и выражения для мгновенных значений тока в ветвях цепи

IR = ,	(34)
IL = ,	(35)
IC = U0··C·cos(t + ).	(36)

При условии, что ·L = , сдвиг фаз между током в неразветвленной части цепи и напряжением равен нулю ( = 0). При этом токи I_L и I_C находятся в противофазе и численно равны. Эти токи могут превосходить ток в подводящих проводах, что требует особенно внимательного соблюдения правил техники безопасности. Такая ситуация называется резонансом токов. При этом происходит периодический обмен энергией между электрическими и магнитными полями в емкости и индуктивности, а источник питания только компенсирует потери энергии на нагревание сопротивления R.

Резонанс токов в цепи с параллельным соединением элементов приводит к тому, что ток во внешней цепи имеет наименьшее значение.

Если убрать сопротивление R, то ток в подводящих проводах будет равен нулю, хотя в контуре, состоящем из L и C, ток может быть очень большим. Это устройство используется в резонансных усилителях, в которых колебательный контур настраивается на частоту сигнала, который требуется усилить.

МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА

Напомним, что мощностью называется физическая величина, численно равная работе в единицу времени. Элементарная работа dA по переносу заряда dq, совершенная за время dt на участке цепи с падением напряжения U, определяется выражением

dA = U·dq.

Тогда мгновенная мощность:

,

(37)

где U(t) и I(t) – мгновенные значения напряжения и силы тока.

В цепях синусоидального переменного тока, содержащих активное сопротивление R, индуктивность L и емкость C, ток, в общем случае, сдвинут по фазе относительно напряжения на угол φ:

U(t) = U₀·cosωt,

I(t) = I₀·cos(ωt + φ),

где U₀ и I₀ – амплитудные значения напряжения и силы тока, ω – круговая частота. Тогда элементарная работа dA за время dt:

dA = U(t)·I(t)·dt = I0·U0·cosωt·cos(ωt + φ)·dt.

(38)

Мгновенная мощность переменного тока также является величиной переменной. Для оценки энергетических свойств электроустановок используется значение средней мощности.

Для определения средней мощности P достаточно подсчитать работу тока за один период колебания T:

(39)

Воспользуемся формулой произведения косинусов:

.

(40)

Интеграл от первого слагаемого в квадратных скобках есть среднее значение косинуса за период и, следовательно, обращается в ноль. Таким образом, получили

.

(41)

Величину P = I·U·cosφ называют активной мощностью или средней мощностью, или просто мощностью переменного тока. Активная мощность в системе СИ измеряется в ваттах (1 Вт = 1 В ´ 1 А). Прибор, предназначенный для регистрации активной мощности, называется ваттметром (подробнее об устройстве и принципе действия ваттметра см. раздел «Ваттметр» в главе «Электроизмерительные приборы»).

Кроме активной мощности в теории переменных токов рассматривают полную (кажущуюся) мощность S = I·U и реактивную мощность Q = I·U·sinj.

Для того чтобы понять смысл реактивной мощности, рассмотрим энергетические процессы в цепи переменного тока, содержащей индуктивность L. В такой цепи потребление мощности в каждый момент времени не сводится только к выделению тепла. В той части периода, где ток нарастает, в катушке индуктивности L возбуждается магнитное поле, на что расходуется энергия источника. Когда же ток начинает уменьшаться, энергия, запасенная магнитным полем катушки, возвращается обратно источнику. Таким образом, индуктивность является то потребителем, то генератором энергии, а в среднем за период расход энергии в индуктивности равен нулю.

Аналогичные колебания происходят в цепи переменного тока, содержащей емкость C. В этом случае энергия запасается в электрическом поле конденсатора. Реактивная мощность Q не совершает никакой полезной работы, однако, она оказывает существенное влияние на режим функционирования электрических цепей. Поэтому расчет проводов и других элементов цепей переменного тока производят, исходя из полной мощности, которая учитывает активную и реактивную составляющие.

Очевидно, что активная P, реактивная Q и полная S мощности имеют одинаковую размерность. Однако в электротехнике, в отличие от единиц активной мощности, для удобства полную мощность принято измерять в вольт-амперах (ВА), а единица измерения реактивной мощности Q – вольт-ампер реактивный (ВАр).

Каким образом величины P, S и Q связаны между собой?

Для наглядности рассмотрим векторную диаграмму напряжений для последовательной цепи переменного тока, содержащей R, L и C, изображенную на рис. 23.

а	б	в

Рис. 23.

Сумма коллинеарных векторов U_L и U_C и перпендикулярного им вектора U_R равна вектору U, который отображает общее падение напряжения в цепи. Он сдвинут относительно вектора тока I на угол j. Вектора U, U_R и (U_L + U_C) образуют треугольник напряжений А0В (прямоугольный), причем катет АВ численно характеризует падение напряжения на чисто реактивной, а 0В – на чисто активной нагрузках:

АВ = U·sinj, 0В = U·cosj.

(42)

Разделив стороны векторного треугольника напряжений на величину силы тока I, получаем треугольник сопротивлений A′0′B′ (рис. 23,б), который уже не будет векторным. Умножив стороны треугольника напряжений на I, получаем треугольник мощностей A″0″B″, также не векторный (рис. 23,в). Очевидно, что эти три треугольника подобны. Сопоставляя стороны треугольника мощностей и треугольника напряжений, заключаем:

0″A″ = I·U = S ← полная мощность,	(43)
0″B″ = I·U·cosj = S·cosj = P ← активная мощность,	(44)
А″B″ = I·U·sinj = S·sinj = Q ← реактивная мощность.	(45)

И, как видно из треугольника A″0″B″, справедливо соотношение:

S2 = P2 + Q2.

(46)

То есть полная мощность является геометрической суммой активной и реактивной мощностей.

Стороны треугольника сопротивлений и треугольника мощностей по построению связаны следующим образом:

P = I2·R,	(47)
Q = I2·(XL – XC) = I2·X,	(48)
S = I2·Z,	(49)

где R – активное сопротивление цепи, X – реактивное сопротивление, X_L = wL – индуктивное сопротивление, X_C = – емкостное сопротивление, – полное сопротивление (импеданс) цепи переменного тока.

Если известны индуктивная Q_Li и емкостная Q_Ci составляющие реактивной мощности и активная P_i мощность каждого i-го потребителя, то полная мощность, на которую должен рассчитываться источник, составляет

.

(50)

Величина cosj, стоящая в выражении для активной мощности (см. формулу (44)), показывает, какая часть полной мощности цепи приходится на долю активной мощности, поэтому cosj называют коэффициентом мощности.

Из формулы (50) видно, что коэффициент мощности можно увеличить, уменьшая второе слагаемое под корнем. Большинство промышленных потребителей (трансформаторы, электродвигатели) потребляют индуктивную реактивную мощность. Для уменьшения такой реактивной мощности параллельно индуктивной нагрузке включают емкость.

МОСТОВОЙ МЕТОД ИЗМЕРЕНИЯ

Мостовые схемы широко применяются в лабораторной практике для измерения электрических характеристик (например, R, C, L) методом сравнения с аналогичными величинами, значения которых известны. Такой метод обладает многими достоинствами, в частности, можно достичь большой точности измерений без использования сложных и дорогостоящих приборов.

Мост Уитстона

Простейшим примером мостовой схемы может служить «мост Уитстона» – схема, впервые разработанная в 1844 г. Чарльзом Уитстоном (Charles Wheatstone, 1802-75) для измерения сопротивлений (рис. 24).

Рис. 24.

Рассмотрим принцип действия мостовой схемы на этом простом примере (рис. 24). Мост Уитстона включает в себя четыре резистора (R₁, R₂, R₃, R₄) – четыре плеча моста, соединенные четырехугольником, источник тока (Е), включенный в одну диагональ моста, и гальванометр (Г), включенный в другую диагональ. Одно из сопротивлений неизвестно, три другие известны и хотя бы одно из них может изменяться. Варьируя величину регулируемого сопротивления, можно добиться такого состояния схемы, при котором разность потенциалов между точками С и D равна 0. Индикатором служит гальванометр, показывающий в этом случае отсутствие тока в ветви CD. В таком состоянии мост называется сбалансированным. Очевидно, что в этом случае

I₁ = I₂, I₃ = I₄, I₁·R₁ = I₄·R₄, I₂·R₂ = I₃·R₃.

Решив эту систему уравнений, получаем:

R₁·R₃ = R₄·R₂ или .

То есть если мост сбалансирован, то между сопротивлениями существует определенное соотношение и, следовательно, неизвестное сопротивление можно выразить через три другие.

Мосты переменного тока

Мостовые схемы можно применять и для измерения таких величин, как емкости (C) и индуктивности (L). Однако для этих целей уже необходимо использовать мосты переменного тока.

По аналогии с мостом Уитстона изобразим схему моста переменного тока (рис. 25).

Рис. 25.

Пусть в мост переменного тока входят четыре элемента (Z₁, Z₂, Z₃, Z₄), один из которых следует определить, а также источник питания (E) и измерительный прибор (V). При отсутствии тока в измерительном приборе мост будет сбалансирован. Так же как для моста Уитстона, в этом случае между импедансами (полными сопротивлениями) плеч моста имеет место соотношение, которое позволяет вычислить искомый импеданс одного из плеч по известным импедансам других плеч. Найдем это соотношение.

Баланс моста достигается только в том случае, когда потенциалы в точках C и D равны друг другу в любой момент времени. Это имеет место при равенстве падений напряжения (U₁ и U₄) на Z₁ и Z₄ как по амплитуде, так и по фазе. При балансе имеем

I₁ = I₂ = ,

I₃ = I₄ = .

Выразим U₁ и U₄:

U₁ = I₁·Z₁ = ,

U₄ = I₄·Z₄ = .

Так как U₁ = U₄, получаем соотношение для импедансов:

Z1·Z3 = Z4·Z2 или .

(51)

Значения величин полных сопротивлений (импедансов) при математических действиях с ними обычно выражают комплексными числами¹:

Z = R + i·X,

где R – активная составляющая полного сопротивления Z, X – реактивная составляющая полного сопротивления Z.

Тогда уравнение (51) примет вид:

(R1 + i·X1)·(R3 + i·X3) = (R2 + i·X2)·(R4 + i·X4).

(52)

Выполнение такого равенства возможно только при одновременном выполнении двух условий – равенстве действительных и мнимых частей, т.е. оно преобразуется в систему из двух уравнений:

R1·R3  X1·X3 = R2·R4  X2·X4,	(53)
X1·R3 + X3·R1 = X2·R4 + X4·R2.	(54)

Отсюда вытекает необходимость выполнения одновременно двух условий. Физический смысл этого требования заключается в том, что для баланса требуется совпадение переменных потенциалов в точках С и D по фазе и по амплитуде. Следовательно, для балансировки такого моста необходимо в общем случае регулировать как минимум два элемента. Также видно, что если импеданс искомого плеча включает в себя реактивную составляющую (C или L), то, по крайней мере, еще одно из плеч тоже должно включать таковую.

При работе с мостами следует иметь в виду, что принципиальная схема является идеализированной. Элементы схемы связаны между собой не только изображенными проводами, но и паразитными емкостями, а иногда и паразитными взаимоиндуктивностями; кроме того, реальные конденсаторы часто обладают «утечкой», т.е. их активное сопротивление не равно нулю. Эти причины, а также неидеальность приборов и т.п., приводят к тому, что на практике обычно невозможно добиться идеального баланса. При работе добиваются не отсутствия тока в ветви CD, а его минимума.

Лабораторная работа 42

ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА

Задачи работы

1. Определение индуктивностей катушек.

2. Определение емкости конденсаторов.

3. Проверка закона Ома для переменного тока.

Физическое обоснование эксперимента

Прежде чем приступать к выполнению работы, необходимо ознакомиться в данном учебном пособии с главой «Переменный электрический ток».

Закон Ома для переменного тока

Закон Ома для переменного тока определяется формулой:

,

где – полное сопротивление цепи, ·L = X_L – индуктивное сопротивление, – емкостное сопротивление,

ω – круговая (циклическая) частота переменного тока (ω = 2·f, где промышленная частота f = 50 Гц), U₀ – амплитуда переменного напряжения.

Определение индуктивностей катушек

Если в цепь переменного тока включить катушку индуктивности, то полное сопротивление цепи:

,

(42.1)

где индекс _пер означает «переменный ток».

Если включить эту же катушку в цепь постоянного тока (ω = 0), то омическое сопротивление катушки будет:

,

(42.2)

где индекс _пост означает «постоянный ток».

Из выражений (42.1) и (42.2) можно, зная полное и омическое сопротивления катушки, найти индуктивное сопротивление

и индуктивность

.

(42.3)

Можно также определить угол сдвига  между напряжением и силой тока в цепи

,

(42.4)

откуда

.

(42.5)

В данной работе две катушки индуктивности намотаны на один стержень. Их омические сопротивления равны r₁ и r₂. При одновременном включении обеих катушек, соединенных последовательно в цепи постоянного тока, их общее сопротивление равно

R = r1 + r2.

При включении обеих катушек в цепь переменного тока, величина индуктивного сопротивления пропорциональна общей индуктивности цепи.

Магнитный поток, пронизывающий катушку, равен:

Φ = L·I.

На рис. 42.1 приведены два способа последовательного соединения катушек – согласованное соединение (а) и бифилярное (б). Буквами Н и К условно обозначены начало и конец обмоток катушек.

Рис. 42.1.

В случае согласованного соединения магнитные потоки, возникающие в катушках, направлены в одну сторону, а в случае бифилярного – навстречу друг другу.

Эксперимент показывает, что магнитный поток, пронизывающий две катушки, оказывается отличным от суммы магнитных потоков, в катушках, включенных по отдельности, при протекании через них такого же тока I. Ток I, протекая через катушку 1, создает в ней поток L₁·I, а в катушке 2 поток М₁₂·I. Аналогично, протекая через катушку 2, он создает в ней поток L₂·I, а в катушке 1 – поток М₂₁·I. Можно показать, что М₁₂ = М₂₁ = М. Величина М называется коэффициентом взаимной индукции. Полный поток в двух катушках равен I·(L₁ + L₂  2M), где знак зависит от того, направлен ли поток М·I одинаково или противоположно потокам L₁·I и L₂·I, а это определяется способом включения катушек (направлением их намотки).

Обозначим L_a – индуктивность двух согласованно включенных катушек. В этом случае потоки, обусловленные взаимной связью катушек (М·I), совпадают по направлению с их собственными потоками (L·I) и, следовательно, L_a равна

La = L1 + L2 + 2M.

(42.6)

В случае бифилярного соединения (рис. 42.1,б), магнитные потоки М·I будут направлены навстречу собственным потокам (L·I) и, следовательно, общая индуктивность L_b при таком включении равна

Lb = L1 + L2 – 2M.

(42.7)

Таким образом, при согласованном включении система обладает большей индуктивностью, чем алгебраическая сумма индуктивностей катушек. При бифилярном включении магнитные потоки, пронизывающие катушки, компенсируют друг друга, вызывая уменьшение индуктивности этих двух катушек. При определенных соотношениях индуктивностей может получиться система с индуктивностью, равной нулю.

Вычитая почленно (42.7) из (42.6), получаем

La – Lb = 4M,

откуда взаимная индуктивность катушек:

.

(42.8)

В данной работе применяется способ измерения сопротивлений (как при переменном, так и при постоянном токе) с помощью амперметра и вольтметра.

Метод исследования и описание установки

Измерение сопротивлений с помощью амперметра и вольтметра

Как уже указывалось в разделе «Электроизмерительные приборы», в зависимости от положения амперметра и вольтметра относительно измеряемого сопротивления при измерении возможны две схемы (рис. 42.2).

Рис. 42.2.

При точных измерениях в обеих схемах собственное сопротивление приборов вызывает дополнительные погрешности, для устранения которых необходимо вносить в результаты следующие поправки.

В случае первой схемы (рис. 42.2 а) вольтметр фактически измеряет не только падение напряжения на сопротивлении Z, но и падение напряжения на амперметре U_A, которое равно произведению сопротивления амперметра на ток:

UA = IA·rA.

Следовательно, полное сопротивление нагрузки Z равно:

или

.

Таким образом, в данной схеме измеряется суммарное сопротивление нагрузки и амперметра. Этой схемой пользуются, когда измеряемое сопротивление велико по сравнению с сопротивлением амперметра (Z >> r_A), и падением напряжения на амперметре можно пренебречь.

Во второй схеме (рис. 42.2, b) параллельно измеряемому сопротивлению Z присоединяется сопротивление вольтметра r_В, и измеряется сопротивление разветвления

.

Этой схемой пользуются в тех случаях, когда измеряемое сопротивление мало по сравнению с сопротивлением вольтметра r_В (Z << r_В), ток вольтметра мал по сравнению с током в искомом сопротивлении, и им можно пренебречь. Следовательно, вторая схема (рис. 42.2,b) целесообразна для измерений относительно малых сопротивлений.

В данной работе применяется цифровой вольтметр с высоким внутренним сопротивлением, поэтому предлагается использовать вторую схему (рис. 42.2,b).

Порядок выполнения работы

В данной работе необходимо экспериментально определить индуктивность каждой обмотки в отдельности и суммарные индуктивности обеих обмоток при их последовательных согласованном и бифилярном включениях.

Определение индуктивностей обмоток

1. Собрать схему (рис.42.3).

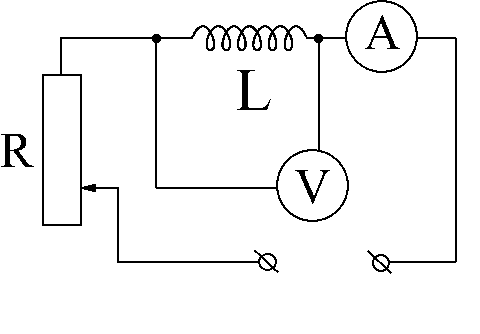
Рис. 42.3.

2. При помощи специального переключателя подать на клеммы сначала переменное, а затем постоянное напряжение.

3. Изменяя силу тока в цепи реостатом R, добиться предельных показаний амперметра. Произвести отсчет показаний амперметра и вольтметра при постоянном и переменном токах. (Измерения для каждого способа включения производятся один раз.)

ВНИМАНИЕ! Во избежание перегревания катушки не следует длительное время оставлять цепь под током. Переключение обмоток катушки производить только при обесточенной схеме. (При этом реостат R каждый раз должен быть введен на максимальное сопротивление.)

4. Вычислить полное сопротивление цепи Z и омическое сопротивление R по формулам (42.1) и (42.2).

На основании полученных данных вычислить индуктивность L, угол сдвига фаз φ и взаимную индуктивность обмоток M по формулам (42.3), (42.5), (42.8).

Определение емкостей конденсаторов

1. Собрать электрическую схему (рис. 42.4), фактически лишь заменив катушку индуктивности из предыдущего задания на конденсатор.

Рис. 42.4.

Реостат R должен быть включен сначала на максимальное сопротивление. Затем подать на схему переменное напряжение.

2. Произвести измерения сначала отдельно для каждой секции батареи конденсаторов C₁ и С₂, а затем при параллельном и последовательном их соединении. Для каждого способа соединения конденсаторов измерение производится один раз. Отсчет снимается при максимальном значении силы тока в цепи.

3. Вычислить емкостное сопротивление XС, поделив показания вольтметра на показания амперметра , а затем определить емкость C по формуле (42.9).

.

(42.9)

Проверка закона Ома для переменного тока

Собрать схему (рис. 42.5).

Рис. 42.5.

В качестве катушки индуктивности L включить обе обмотки индуктивности при их последовательном согласованном соединении (как на рис. 42.1,а). Включить в схему одну из двух конденсаторов (C₁ или C₂).

В цепь переменного тока последовательно включены активное сопротивление (омическое сопротивление катушки индуктивности), индуктивное и емкостное сопротивления. В этом случае полное сопротивление цепи можно вычислить по формуле

(42.10)

или определить из эксперимента по измеренным значениям напряжения и тока в цепи:

.

(42.11)

Уменьшая сопротивление реостата, добиться предельного показания амперметра. Записать показания амперметра (ток I) и вольтметра (напряжение U), и вычислить значение Z по формуле (42.11).

Подставляя ранее полученные значения R, X_L и X_C в формулу (42.10), вычислить Z и сравнить ее с величиной, полученной по формуле (42.11). В случае выполнения закона Ома для переменного тока оба значения Z должны совпадать (в пределах погрешностей измерений).

Обработка результатов измерений

Относительная погрешность электроизмерительных приборов, согласно формуле (6), определяется по классу точности прибора:

,

где _{КЛ Т} – класс точности прибора, I_НОМ – номинальное (максимальное) значение тока или напряжения, которое может быть измерено по используемой шкале прибора (предел измерения прибора), I_ИЗМ – измеряемое значение тока или напряжения.

Погрешность косвенных измерений вычисляется по формулам переноса ошибок.

Содержание отчета

1. Электрические схемы измерений индуктивности катушек, емкости конденсаторов и схема для проверки закона Ома.

2. Сводная таблица экспериментальных данных.

3. Расчет индуктивностей L₁, L₂, L_a, L_b.

4. Расчет угла сдвига фаз между напряжением и силой тока для измеренных индуктивностей по формуле (42.5) (по указанию преподавателя).

5. Расчет коэффициента взаимной индуктивности M для двух обмоток по формуле (42.8).

6. Расчет неизвестных емкостей C₁ и C₂, а также общей их емкости при параллельном и последовательном их соединениях, и сравнение расчетных значений с полученными в эксперименте.

7. Расчет полного сопротивления цепи по формулам (42.11) и (42.10) при проверке закона Ома.

8. Расчет абсолютной погрешности измерения полного сопротивления цепи при проверке закона Ома.

Контрольные вопросы

• Что такое ω и чему она равна?

• При измерениях индуктивностей катушек ток в них отстает от напряжения по фазе или опережает его?

Лабораторная работа 43

ИССЛЕДОВАНИЕ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМИ И ИНДУКТИВНЫМИ СОПРОТИВЛЕНИЯМИ

Цель и задачи работы

Цель работы:

Показать, что в отличие от цепей постоянного тока, в цепях переменного тока при параллельном включении активного и индуктивного сопротивлений векторная сумма токов ветвей меньше их алгебраической суммы, а при последовательном включении – векторная сумма напряжений на отдельных участках цепи меньше их алгебраической суммы. Это обусловлено возникновением сдвига фаз между током и напряжением при наличии в цепи реактивной нагрузки (в данной работе – катушки индуктивности).

При параллельном включении активного и реактивного сопротивлений токи в этих ветвях не совпадают по фазе. При их последовательном включении возникает сдвиг фаз между падениями напряжения на различных сопротивлениях. (См. «Понятие о векторных диаграммах»).

Задачи работы:

1. Построение векторных диаграмм напряжений и токов и вычисление индуктивности цепи.

2. Построение треугольников сопротивлений.

3. Определение активной, реактивной и полной мощности цепей.

4. Построение треугольников мощностей.

Физическое обоснование эксперимента

Прежде чем приступить к выполнению работы, необходимо ознакомиться с главами «Переменный электрический ток», «Построение векторных диаграмм», «Мощность переменного тока».

Описание установки

В работе необходимо последовательно произвести измерения параметров двух различных схем (рис. 43.1 и рис. 43.2). Обе схемы составляются из одних и тех же элементов, но в первом опыте активное и индуктивное сопротивления включаются последовательно, а во втором – параллельно.

Рис. 43.1.

Рис. 43.2.

В качестве активного сопротивления используется ламповый реостат (на схеме обозначен R₂). Его сопротивление изменяется путем включения и выключения ламп накаливания.

В качестве реактивного сопротивления используется катушка индуктивности L, индуктивность которой можно изменять, вдвигая и выдвигая сердечник.

Реостат R₀ регулирует входное напряжение U₀, измеряемое вольтметром V₀. Ваттметр W измеряет активную мощность P. Амперметр А₀ измеряет ток I₀. Реостат R₁ позволяет дополнительно увеличивать активное сопротивление участка цепи, включающего индуктивность.

Вольтметры V₁ и V₂ в первой схеме измеряют падения напряжения U₁ и U₂ на индуктивном и чисто активном сопротивлениях соответственно. Амперметры А₁ и А₂ во второй схеме измеряют токи: I₁ – протекающий по ветви содержащей индуктивность, и I₂ – протекающий по ветви, состоящей из чисто активного сопротивления.

В этой работе наиболее наглядные результаты можно получить, если на входах, как первой, так и второй схем установить приблизительно одинаковые значения I₀, U₀ и P.

Порядок выполнения работы

Опыт 1

1. Собрать схему (рис. 43.1).

2. В собранной схеме с помощью реостатов установить значения U₀₁, I₀₁, P₁ по указанию преподавателя. Установку следует производить, регулируя R₀, L, R₁ и R₂.

3. Записать результаты измерений в табл. 43.1 (Опыт 1).

Опыт 2

4. Собрать схему (рис. 43.2).

5. Установить значения U₀₁, I₀₁, и P₁ такие же, как в первом опыте или близкие к ним U₀₂, I₀₂, и P₂, если не удастся добиться тех же значений. Установку производить, регулируя L, R₁ и R₂.

6. Записать результаты измерений в табл. 43.1 (опыт 2).

Обработка результатов измерений

1. По результатам Опыта 1 построить векторную диаграмму напряжений (рис. 43.3, а).

Рис. 43.3.

2. По результатам Опыта 2 построить векторную диаграмму токов (рис. 43.4, а).

Рис. 43.4.

3. В соответствии с приведенными ниже указаниями произвести расчеты, результаты которых занести в табл. 43.2 и 43.3.

Примечание. Все векторные диаграммы строятся обязательно на миллиметровой бумаге в удобном масштабе, который указывается на диаграмме.

Таблица 43.1

Опыт 1 (рис. 43.1)					Опыт 2 (рис. 43.2)
U01, B	I01, A	P1, Bт	U1, B	U2, B	U02, B	I02, А	P2, Bт	I1, A	I2, A

Таблица 43.2.

S1, Bт	cosφ1	φ1	UR, B	UL, B	R, Ом	XL, Ом	Z, Ом	L, Гн	P1, Вт	Q1, Вт

Таблица 43.3.

S2, Bт	cosφ2	φ2	Ig, A	IL, A	L, Гн	P2, Вт	Q2, Вт

Указания по расчетам и построению диаграмм

При построении векторной диаграммы напряжений (рис. 43.3,а) исходным считается вектор тока I₀. Вектор напряжения U₂ совпадает по фазе с вектором I₀, следовательно, его величину в выбранном масштабе следует отложить на диаграмме вдоль направления вектора тока. Участок цепи, на котором измерено U₁, включает и активное и индуктивное сопротивления, поэтому вектор U₁ опережает по фазе вектор тока, но на угол меньший, чем , т.е. будет направлен влево вверх от конца вектора U₂. Чтобы построить вектор U₁ на диаграмме необходимо с помощью циркуля провести дугу радиуса равного модулю U₁ (в выбранном масштабе) с центром в точке, совпадающей с концом вектора U₂. А из начала вектора U₂ – дугу радиусом, равным модулю U₀. Пересечение этих двух дуг и определит направления векторов U₀ и U₁. Далее вектор U₀ раскладывается на два составляющих вектора: U_R, совпадающий по фазе с током, и U_L, опережающий ток на .

При построении векторной диаграммы токов (рис. 43.4,а) за исходный вектор принимается вектор напряжения U₀. Вектор тока I₂ совпадает по фазе с вектором U₀ и, следовательно, его (в определенном масштабе) следует построить в том же направлении. Так как при индуктивном сопротивлении участка цепи вектор тока отстает от вектора приложенного напряжения, то вектор тока I₁ будет отставать по фазе от вектора U₀. Но поскольку этот участок включает и активное сопротивление, то угол отставания меньше . Следовательно, I₁ направлен вправо вверх от конца вектора I₂. Чтобы его построить, надо провести дугу радиусом равным модулю I₁ с центром в точке совпадающей с концом I₂, из начала I₂ – дугу радиусом I₀. Пересечение дуг определит направления векторов I₁ и I₀.

Далее вектор I₀ раскладывается на два составляющих вектора: I_R, совпадающий по фазе с вектором U, и вектор I_L, отстающий от этого вектора на угол .

1. По данным табл. 43.1 определить:

а) Полную мощность цепи:

S₁ = U₀₁·I₀₁.

б) Коэффициент мощности цепи и угол φ₁:

cosφ₁ = ; φ₁ = arccos

(полученное значение φ₁ сравнить с углом φ₁ на векторной диаграмме).

в) Из векторной диаграммы (рис. 43.3,а) определить активную и реактивную составляющие напряжения U_R = U₂ + U_r = I₀₁·R и U_L = I₀·X_L.

г) Вычислить стороны треугольника сопротивлений R, X_L, Z: активное сопротивление R = U_R/I₀₁, индуктивное X_L = U_L/I₀₁, полное Z = U₀₁/I₀₁. Построить треугольник сопротивлений в удобном масштабе (рис. 43.3,б). Следует обратить внимание на то, что полное активное сопротивление R складывается из сопротивления лампового реостата, реостата R₁ и активного сопротивления соленоида.

д) Вычислить индуктивность цепи по формуле .

е) Вычислить активную, реактивную и полную мощности по формулам: P₁ = I₀₁²·R, Q₁ = I₀₁²·X_L, S₁ = I₀₁²·Z (P₁ сравнить со значением, определенным по ваттметру, S₁ сравнить со значением, полученным в пункте a). Построить в удобном масштабе треугольник мощностей (рис. 43.3,в).

Все результаты расчета занести в табл. 43.2.

2. По данным табл. 43.1 (опыт 2) определить:

а) Полную мощность цепи:

S₂ = U₀₂·I₀₂.

б) Коэффициент мощности цепи и угол φ:

cosφ₂ = ; φ₂ = arccos

(полученное значение φ₂ сравнить с углом φ₂ на векторной диаграмме).

в) Из векторной диаграммы (рис. 43.4,а) определить составляющие тока I_L и I_R, как длины векторов I_L, отстающего от вектора U на угол и I_R, совпадающего с U по фазе.

г) Вычислить индуктивность цепи:

.

д) Построить треугольник мощностей (рис. 43.4,в) по значениям:

P₂ = U₀₂·I_R, Q₂ = U₀₂·I_L, S₂ = U₀·I₀

(P₂ сравнить со значением, определенным по ваттметру).

Результаты расчета записать в табл. 43.3.

Лабораторная работа 44

ИЗМЕРЕНИЕ ЕМКОСТЕЙ КОНДЕНСАТОРОВ С ПОМОЩЬЮ МОСТА ПЕРЕМЕННОГО ТОКА

Задачи работы

1. Измерение величин нескольких емкостей.

2. Расчет емкостных сопротивлений.

Физическое обоснование эксперимента

Прежде чем приступать к выполнению работы, необходимо ознакомиться в данном учебном пособии с главой «Мостовой метод измерений».

Метод исследования и описание установки

Рис. 44.1.

Экспериментальная установка представляет собой мостовую схему, изображенную на рис. 44.1. Здесь R₃ и R₂ – магазины сопротивлений. С₀ – магазин емкостей, С_X – конденсатор, емкость которого требуется определить. В качестве источника питания используется звуковой генератор ГЗ-34. В другую диагональ моста включен милливольтметр В3-39.

Как известно, конденсаторы обладают емкостным сопротивлением , где C – емкость,  = 2·f – круговая частота (f – частота переменного тока). Полные сопротивления плеч такого моста представляют собой соответственно:

Z1 = X1 =	(R1 = 0);
Z2 = R2	(X2 = 0);
Z3 = R3	(X3 = 0);
Z4 = X4 =	(R4 = 0).

Запишем применительно к такой схеме систему уравнений (53) и (54), которая должна выполняться при балансе моста. Видно, что уравнение (53) выполняется автоматически, так как R₁ = 0, X₂ = 0, X₃ = 0, R₄= 0. А уравнение (54) принимает вид

X₁·R₃ = X₄·R₂.

Подставив в него значения Х₁ и Х₂, получаем

.

(44.1)

Таким образом, если мост сбалансирован, то С_x можно определить, зная величины С₀, R₃ и R₂.

Порядок выполнения работы

1. Собрать электрическую схему в соответствии с рис. 44.1, включив в нее один из исследуемых конденсаторов.

2. Установить на генераторе частоту 1000 Гц.

3. Установить на магазинах сопротивлений R₃ и R₂ по 500Ом.

4. Установить на магазине емкостей С₀ = 0.

5. Установить предел измерений вольтметра 10 В.

6. Проверить электрическую схему.

7. Включить генератор и вольтметр (после проверки схемы лаборантом), дать приборам прогреться.

8. Изменяя величину емкости магазина емкостей С₀, добиться минимального показания вольтметра. При этом, так как В3-39 – прибор многопредельный, то, по мере уменьшения его показаний, следует увеличивать его чувствительность (уменьшать пределы измерений).

9. Повторить балансировку, изменяя сопротивления R₃ и R₂ или частоту (по указанию преподавателя).

10. Провести аналогичные измерения для других неизвестных конденсаторов. Рассчитать их емкостные сопротивления.

11. В данной работе требуется определить, также, емкости и емкостные сопротивления некоторых (по указанию преподавателя) комбинаций конденсаторов при их параллельном и последовательном соединениях. Полученные значения сравнить со значениями, рассчитанными по формулам для данных комбинаций.

Содержание отчета

1. Схема установки.

2. Результаты всех измерений (желательно в виде таблицы).

3. Расчет значений емкостей и емкостных сопротивлений всех исследованных конденсаторов и их комбинаций.

4. Расчет теоретических значений емкостей исследованных комбинаций конденсаторов. Сравнение теоретических результатов с экспериментальными.

5. Расчеты погрешности измерений двумя способами: на основании класса точности приборов и, где возможно, учитывая разброс результатов измерений при варьировании сопротивлений.

6. Окончательные результаты с указанием погрешностей.

Контрольные вопросы

• От каких параметров зависит емкостное сопротивление?

• В чем принципиальное различие мостов постоянного и переменного тока?

• Каков сдвиг по фазе на емкости (индуктивности) между током и напряжением?

• В каком случае общая емкость (емкостное сопротивление) больше: при параллельном или при последовательном включении конденсаторов?

Лабораторная работа 45

ИЗМЕРЕНИЕ ИНДУКТИВНОСТЕЙ КАТУШЕК С ПОМОЩЬЮ МОСТА ПЕРЕМЕННОГО ТОКА

Задачи работы

1. Измерение величины индуктивностей нескольких катушек.

2. Расчет их активных и реактивных сопротивлений.

Физическое обоснование эксперимента

Прежде чем приступать к выполнению работы, необходимо ознакомиться в данном учебном пособии с главой «Мостовой метод измерений».

Метод исследования и описание установки

Экспериментальная установка представляет собой мостовую схему, изображенную на рис.45.1. Здесь R₁, R₂, R₃ и R₄ – магазины сопротивлений, L₀ – эталонная катушка с известной индуктивностью L₀ и известным активным сопротивлением r₀, L_X – исследуемый соленоид, для которого требуется определить индуктивность L_X и активное сопротивление r_X. В качестве источника питания в одну из диагоналей моста включается либо звуковой генератор Гз, либо источник постоянного тока Е (переключение производится ключом К₂). Ключ К служит для замыкания цепи гальванометра при измерении на постоянном токе.

В другую диагональ моста (CD) могут быть включены либо гальванометр Г (в случае измерений на постоянном токе), либо ламповый милливольтметр В3-39 (в случае измерений на переменном токе). Переключение производится ключом К₁.

Как известно, сопротивление соленоида имеет активную и реактивную составляющие, и, в общем случае, равно:

,

где Х_L = L – индуктивное сопротивление,  = 2f – круговая частота (f – частота переменного тока).

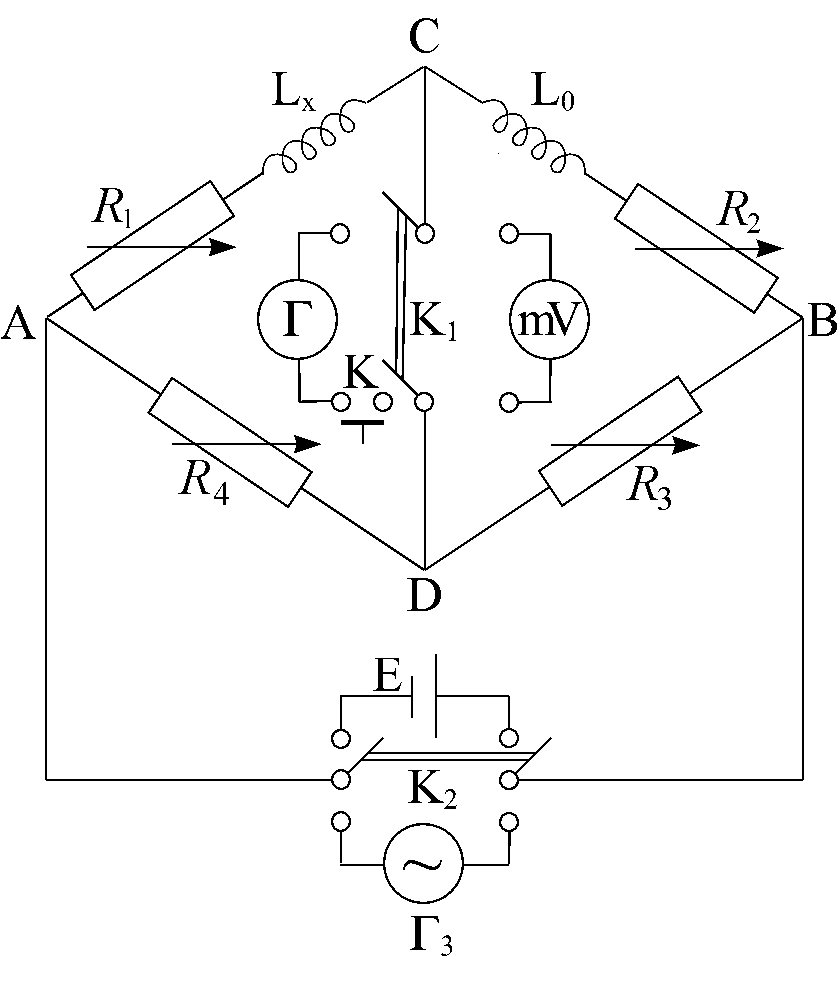
Рис. 45.1.

Или, используя способ записи с помощью комплексных чисел:

Z = r + i··L.

Полные сопротивления плеч такого моста представляют собой соответственно:

Z₁ = R₁ + r_X + i··L_X,

Z₂ = R₂ + r₀ + i··L₀,

Z₃ = R₃ (X₃ = 0),

Z₄ = R₄ (X₄ = 0).

Запишем, применительно к такой схеме, систему уравнений (53) и (54), которая должна выполняться при балансе моста. Так как X₄ = 0 и X₃ = 0, уравнения (53) и (54) принимают вид

(R1 +rX)·R3 = (R2 + r0)·R4 ,	(45.1)
LX·R3 = L0·R4.	(45.2)

Перепишем получившуюся систему уравнений в более наглядном виде и проанализируем ее¹:

,	(45.3)
.	(45.4)

Если в плечи моста, содержащие индуктивности, не включать дополнительные сопротивления (R₁ = R₂ = 0), то одновременное выполнение этих двух равенств в общем случае невозможно. Такое совпадение означало бы, что активные сопротивления катушек и их индуктивности находятся в одинаковом соотношении, что весьма маловероятно, так как активное сопротивление катушки и ее индуктивность определяются различными физическими причинами. Для балансировки рассматриваемого моста необходимо подключать дополнительные активные сопротивление R₁ и R₂ (или хотя бы одно из них). При этом выбор того плеча, в которое надо включать сопротивление, определяется соотношением между включенными в мост индуктивностями и их активными сопротивлениями.

Выполнение уравнений (45.3) и (45.4) соответствует балансу моста, т.е. отсутствию разности потенциалов между точками C и D в любой момент времени. Анализ уравнений показывает, что для достижения этого необходимо регулировать, как минимум, два параметра R₁ и/или R₂ и отношение R₄/R₃. Практически это довольно сложно в условиях, когда в плечах моста уже есть неизменные сопротивления (r₀ + i··L₀) и (r_X + i··L_X).

Кроме того, в диагонали моста CD возможно получение минимумов напряжения и не соответствующих состоянию баланса в случае, когда потенциалы в точках C и D не совпадают по фазе. Дополнительно затрудняет измерения то обстоятельство, что, и при условии выполнения уравнений (45.3) и (45.4) практически не достигается полное отсутствие тока, а только более «глубокий» минимум. Вспомогательное уравновешивание моста на постоянном токе позволяет проверить достижение состояния истинного баланса, а кроме того, упрощает поиски «истинного», наиболее глубокого минимума.

Отсутствие тока в диагонали CD при балансе на постоянном токе свидетельствует о выполнении уравнения (45.3). Если минимум сигнала в CD на переменном токе получен при том же отношении R₄/R₃, что и на постоянном токе, то это будет означать, что оба уравнения выполняются и баланс достигнут.

Используя полученные значения сопротивлений R₁, R₂, R₃ и R₄, можно из уравнения (45.3) вычислить значение активного сопротивления исследуемой катушки, а из уравнения (45.4) – значение ее индуктивности.

Порядок выполнения работы и обработка результатов измерений

1. Собрать электрическую схему в соответствии с рис. 45.1, включив в нее один из исследуемых соленоидов. На генераторе уже установлена частота, равная 1000 Гц.

2. Установить на магазинах сопротивлений: R₁ = R₂ = 0, R₃ = R₄ = 500 Ом.

3. Установить предел измерений вольтметра 30 В.

4. Перевести ключи К₁ и К₂ в положение «переменный ток». Включить генератор и вольтметр (после проверки схемы), дать приборам прогреться.

5. Провести первичную балансировку на переменном токе, т.е. изменяя величины сопротивлений R₃ и R₄, добиться минимального показания вольтметра. При этом, так как В3-39 – прибор многопредельный, то, по мере уменьшения его показаний, следует увеличивать его чувствительность (уменьшать пределы измерений). Записать получившиеся значения R₃ и R₄.

6. Переключить схему на постоянный ток (ключи К₁ и К₂ в положение «постоянный ток»). Изменяя R₃ и R₄, добиться баланса (отсутствия тока в гальванометре) при постоянном токе. При измерении замыкать ключ К. Вспомним рабочую систему уравнений, которые должны выполняться одновременно: (R₁ + r_X)/(R₂ + r₀) = R₄/R₃ и L_X/L₀ = R₄/R₃. Первое из этих уравнений выполняется и при балансе на постоянном токе, так как в него входят только чисто активные сопротивления. Сравним получившиеся в эксперименте отношения (R₄/R₃)_пост и (R₄/R₃)_перем. Чтобы оба уравнения выполнялись одновременно, необходимо изменить R₁ или R₂, а так как и R₁, и R₂ пока равны нулю, необходимо сделать одно из них отличным от нуля. В зависимости от соотношения между (R₄/R₃)_пост и (R₄/R₃)_перем, надо вводить или R₁, или R₂. Из системы уравнений видно, что для того, чтобы оба уравнения выполнялись при одном и том же отношении R₄/R₃, надо:

если (R₄/R₃)_пост > (R₄/R₃)_перем, то увеличить R₂,

если (R₄/R₃)_пост < (R₄/R₃)_перем, то увеличить R₁.

7. Восстановить на магазинах сопротивлений R₃ и R₄ значения, найденные при балансировке на переменном токе. И, изменяя R₁ или R₂ (в соответствии с выше сказанным), вновь добиться баланса на постоянном токе.

8. Переключить схему на переменный ток (ключи К₁ и К₂ в положение «переменный ток»). Изменяя R₃ и R₄, вновь добиться баланса на переменном токе.

9. Вновь переключить схему на постоянный ток (ключи К₁ и К₂ в положение «постоянный ток»). Изменяя R₁ или R₂, добиться баланса на постоянном токе.

10. Повторять операции 8 и 9 до тех пор, пока баланс не будет выполняться одновременно на постоянном и переменном токе (при одних и тех же значениях R₁, R₂, R₃ и R₄). Из уравнений (45.3) и (45.4), используя полученные значения величин R₁, R₂, R₃ и R₄, рассчитать величины L_X и r_X . Параметры эталонного соленоида: L₀ = 1 Гн и r₀ = 222,7 Ом.

11. Провести аналогичные измерения для других соленоидов (по указанию преподавателя). Рассчитать их индуктивности и активные сопротивления.

В данной работе рекомендуется определить также индуктивности и активные сопротивления некоторых (по указанию преподавателя) комбинаций соленоидов при их согласованном и бифилярном соединениях. В этом случае требуется дополнительно рассчитать коэффициенты взаимоиндукции М и связи К этих катушек из следующих формул (подробнее см. Лабораторную работу 42):

L = L₁ + L₂  2M,

.

Здесь знак «плюс» берется при согласованном, а «минус» – при бифилярном включении катушек.

Содержание отчета

1. Схема установки.

2. Результаты всех измерений в виде таблицы.

3. Расчет значений индуктивностей и активных сопротивлений всех исследованных соленоидов и их комбинаций.

4. Расчет индуктивностей и активных сопротивления комбинаций соленоидов при их согласованном и бифилярном соединениях, коэффициента взаимоиндукции и коэффициента связи (по указанию преподавателя).

5. Расчеты погрешностей измерений на основании класса точности приборов.

6. Окончательные результаты с указанием погрешностей.

Контрольные вопросы

• От каких параметров зависит индуктивное сопротивление?

• В чем принципиальное различие мостов постоянного и переменного тока?

• Каков сдвиг по фазе на емкости (индуктивности) между током и напряжением?

• В каком случае общая индуктивность больше: при согласованном или при бифилярном включении соленоидов?

Лабораторная работа 46

ИЗУЧЕНИЕ РАБОТЫ ТРАНСФОРМАТОРА

Задачи работы

1. Изучение различных режимов работы трансформатора.

2. Расчет величины параметров, характеризующих трансформатор.

Физическое обоснование эксперимента

Цель работы: изучить в различных режимах работу трансформатора и рассчитать величины характеризующих трансформатор параметров.

Прежде чем приступить к выполнению работы, необходимо ознакомиться с введениями по темам «Переменный электрический ток», «Мощность переменного тока».

Трансформатором называется устройство, в котором переменный ток одного напряжения преобразуется в переменный ток той же частоты, но другого напряжения. Его работа основана на явлении электромагнитной индукции: при изменении потока магнитной индукции Φ, пронизывающего замкнутый проводящий контур, в нем возникает электрический ток. Направлен этот ток, называемый индукционным, всегда так, чтобы максимально противодействовать вызывающей его причине. ЭДС индукции Ε определяется уравнением Фарадея  Ленца:

.

Трансформатор состоит из замкнутого ферромагнитного сердечника (магнитопровода), на который намотаны две (или более) обмотки (рис. 46.1). Обмотки эти обычно электрически изолированы друг от друга. Сердечник собирается из отдельных листов железа (трансформаторной стали с малой коэрцитивной силой), разделенных изолирующими слоями лака, бумаги или пластика. Применение таких наборных сердечников уменьшает величину индукционных (вихревых) токов, возникающих в них, что увеличивает КПД трансформатора.

Рис. 46.1.

Первичной называется обмотка трансформатора, соединенная с внешним источником переменного напряжения. Соответственно первичными именуются все величины, относящиеся к этой обмотке – число витков n₁, напряжение U₁, сила тока I₁, мощность Р₁ и т.д. Обмотка, с которой снимается электроэнергия, и, соответственно, относящиеся к ней величины, называются вторичными – n₂, U₂, I₂, Р₂, R₂, X_L2, Z₂.

Ток I₁ в первичной обмотке трансформатора возникает под действием первичного синусоидального напряжения U₁. Этот ток порождает в магнитопроводе переменный магнитный поток: Φ = Φ_m·sint. Этот поток, пронизывая обе обмотками трансформатора, индуцирует в них ЭДС, мгновенные значения которых будут по закону Фарадея–Ленца равны:

e1 = –n1· = – ·n1·Φm·cost = Em1·sin,	(46.1)
e2 = –n2· = – ·n2·Φm·cost = Em2·sin.	(46.2)

Из формул видно, что ЭДС индукции в первичной и вторичной обмотках отстает по фазе от магнитного потока. Отношение мгновенных, амплитудных и действующих значений этих ЭДС равно отношению чисел витков обмоток трансформатора:

.

(46.3)

Отношение K называется коэффициентом трансформации. Это важнейшая характеристика трансформатора. Если устройство трансформатора таково, что K  1 (т.е. вторичное напряжение U₂ больше первичного U₁), то трансформатор называется повышающим, если K  1 (т.е. U₂  U₁), то – понижающим.

Коэффициентом полезного действия (КПД) трансформатора называют отношение мощности, выделяемой на нагрузке, к мощности, потребляемой первичной обмоткой от сети:

.

(46.4)

При номинальной (т.е. той, на которую он рассчитан) нагрузке мощного трансформатора его КПД очень высок – до 95%. Он существенно понижается лишь при малых нагрузках или у маломощных трансформаторов.

Рассмотрим работу трансформатора с точки зрения закона сохранения энергии. Из мощности Р₁, подведенной к первичной обмотке, часть P_дж1 (джоулевы потери) расходуется на нагревание проводов первичной обмотки, а часть Р_ст затрачивается в сердечнике на потери от перемагничивания (гистерезиса) и вихревых токов. Остальная мощность передается во вторичную обмотку:

Р₁₂ = Р₁ – Р_дж1 – Р_ст.

Во вторичной обмотке часть мощности Р_дж2 теряется на нагревание проводов, а оставшаяся Р₂ передается во вторичную цепь:

Р₂ = Р₁₂ – Р_дж2 = Р₁ – Р_дж1 – Р_ст – Р_дж2.

В реальных трансформаторах часть магнитного потока замыкается вне магнитопровода, образуя потоки рассеяния. Однако в современных трансформаторах эти потоки малы по сравнению с основным потоком в магнитопроводе, в результате чего потери передаваемой мощности минимальны.

Напряжения, токи и ЭДС в обмотках (без учета ЭДС, наводимых потоками рассеяния) связаны соотношениями:

u₁ + e₁ = i₁·r₁

u₂ + i₂·r₂ = e₂.

Если напряжение u₁, приложенное к первичной обмотке, синусоидальное, то магнитный поток Φ и ЭДС e₁ и e₂ будут также синусоидальными, поэтому при анализе работы трансформатора удобно рассматривать действующие значения ЭДС Ε₁ и Ε₂, напряжений U₁ и U₂ и токов I₁ и I₂. Омические сопротивления обмоток обычно малы, и ими в ряде случаев можно пренебречь.

Основные характеристики трансформатора и его параметры могут быть изучены в опытах холостого хода трансформатора, в опытах его рабочего режима и в опытах короткого замыкания.

Режим холостого хода

Холостым ходом трансформатора называется такой режим его работы, когда к зажимам первичной обмотки подводится переменное напряжение, а цепь вторичной обмотки разомкнута.

В режиме холостого хода ток в первичной обмотке I₁^хол очень мал, а сопротивление первичной обмотки у трансформаторов обычно тоже мало. Следовательно, падение напряжения на первичной обмотке при холостом ходе пренебрежимо мало, т.е. можно считать, что U₁ = е₁. Во вторичной обмотке в режиме холостого хода напряжение в точности равно ЭДС (U₂^хол = е₂), так как обмотка разомкнута. Эти факты позволяют определять в режиме холостого хода коэффициент трансформации

.

(46.5)

Мощность, потребляемая трансформатором при холостом ходе, затрачивается на потери P_ст в стальном сердечнике (на его перемагничивание и на вихревые токи Фуко в нем) и на нагревание P_дж (джоулевы потери) одной лишь первичной обмотки (I₁^хол)²r₁, где r₁ – омическое сопротивление первичной обмотки. Однако в этом режиме потери на джоулево нагревание обмотки ничтожны по сравнению с потерями в стали (исключение составляют лишь трансформаторы малой мощности). Следовательно, вся мощность холостого хода трансформатора практически затрачивается лишь на потери в стали, и поэтому опыт холостого хода позволяет определить потери в стали трансформатора.

Рабочий режим

В рабочем режиме трансформатора во вторичную обмотку включается (обычно омическая) нагрузка. Во вторичной цепи трансформатора ЭДС индукции Ε₂ играет роль источника энергии. Она создает ток I₂, который порождает в сердечнике вторичный магнитный поток. Согласно правилу Ленца, этот поток направлен противоположно основному потоку, индуцирующему ЭДС Ε₂, стремясь его уменьшить. А это, опять же по правилу Ленца, приводит к увеличению первичного тока при том же самом напряжении в первичной цепи настолько, чтобы восстановить первоначальный магнитный поток, при котором существует равновесие в первичной цепи между напряжением U₁ и наведенной ЭДС Ε₁ (U₁  Ε₁).

Таким образом, всякое изменение силы тока во вторичной обмотке трансформатора вызывает соответствующее изменение силы тока в первичной, но практически не влияет на амплитуду основного магнитного потока Φ. Следовательно, пока не изменяется первичное напряжение U₁ трансформатора, остается неизменным и его основной магнитный поток Φ, что характерно для рабочего режима трансформатора. Изменением сопротивления нагрузки можно изменять ток во вторичной обмотке и тем самым при постоянном напряжении U₁ варьировать мощность, выделяющуюся во вторичной обмотке (отбираемую от трансформатора потребителем).

Электрическая мощность, подаваемая в первичную цепь трансформатора и измеряемая ваттметром, включенным в эту цепь, равна

P1 = I1·U1·cos1.

(46.6)

Измерив напряжение и ток в первичной обмотке, можно определить коэффициент мощности (см. «Введение») первичной цепи:

.

(46.7)

Аналогичные измерения, проведенные для вторичной обмотки, дают

P2 = I2·U2·cos2,	(46.8)
.	(46.9)

КПД трансформатора будет выражаться формулой

.

КПД в зависимости от отбираемой из вторичной цепи мощности будет изменяться. График этой зависимости  = f(I₂) обладает максимумом. КПД трансформатора, как показывает теория, достигает максимума в тот момент, когда джоулевы потери в обмотках P_дж равны потерям в стальном сердечнике трансформатора P_ст.

Режим короткого замыкания

Режимом короткого замыкания трансформатора называется режим, при котором вторичная обмотка замкнута накоротко или на очень малое сопротивление. Короткое замыкание в условиях эксплуатации создает аварийное состояние, поскольку вторичный ток, а следовательно, и первичный, увеличиваются в несколько десятков раз по сравнению с номинальными, что может вызвать разрушение трансформатора. Поэтому в цепях с трансформатором должна быть предусмотрена защита, которая при коротком замыкании автоматически отключает трансформатор.

В лабораторных условиях можно провести испытательные опыты по короткому замыканию трансформатора. Для этого опыта на первичную обмотку подается очень маленькое (близкое к нулю) напряжение, а зажимы вторичной обмотки трансформатора замыкаются накоротко. Таким образом, в режиме короткого замыкания на трансформатор подается очень маленькая мощность. Посредством вольтметра, амперметра и ваттметра измеряются напряжение U₁^кор, ток I₁^кор и мощность Р₁^кор, потребляемая трансформатором. При очень малом напряжении U₁ и малом токе первичной обмотки в сердечнике возбуждаются малые магнитные потоки Φ_кз (основной магнитный поток сцепления уже сравним с магнитным потоком рассеяния, которым пренебрегали в рассматриваемых ранее электромагнитных процессах). Малость магнитных потоков приводит к тому, что потери в стали сердечника становятся близки к нулю (Р_ст  0). Вместе с тем при опыте короткого замыкания величины сил токов, а значит, и потери в проводниках обмоток такие же, как и при нагрузке. На этом основании можно считать, что при опыте короткого замыкания вся мощность Р₁^кор затрачивается на джоулевы потери в проводниках обмоток трансформатора:

Р₁^кор = I₁² r₁ + I₂²·r₂.

Иногда трансформатор представляют в виде упрощенной эквивалентной схемы, для которой используется понятие активного сопротивления. Активное сопротивление трансформатора или сопротивление короткого замыкания R_КЗ определяется в режиме короткого замыкания как:

.

(46.10)

Опыт короткого замыкания служит также контрольным опытом для определения коэффициента трансформации. Так как в этом режиме суммарный магнитный поток в сердечнике очень мал, то в первом приближении намагничивающая сила в первичной цепи I₁·n₁ уравновешивается размагничивающим действием вторичного тока I₂·n₂:

I₁·n₁  I₂·n₂.

Следовательно:

.

(46.11)

Порядок выполнения работы

Рис. 46.2.

1. Изучить схему (рис. 46.2), собранную на лабораторном столе.

2. Провести опыт холостого хода трансформатора.

Для этого:

а) Проверить положение ключей К₁ и К₂ во вторичной цепи. Они должны быть разомкнуты.

б) Установить напряжение U₁ = 120 В в первичной цепи с помощью лабораторного автотрансформатора (ЛАТРа)¹.

в) Снять показания всех приборов и записать их в первую строку Таблицы 46.1.

3. Выполнить измерения в рабочем режиме трансформатора.

Для этого:

а) Установить максимальное сопротивлении во вторичной цепи и замкнуть ключ К₁.

б) Напряжение в первичной цепи U₁ = 120 В поддерживать постоянным в течение опыта.

в) Изменять ток I₂ вторичной цепи от 1 до 10 A через 1 A, изменяя сопротивление нагрузки с помощью реостатов R₁ и R₂.

г) Показания всех приборов свести в табл. 46.1.

4. Провести опыт короткого замыкания трансформатора.

Для этого:

а) Напряжение в первичной цепи установить равным 0 (U₁ = 0 В)

б) Только после того, как убедитесь, что вольтметр первичной цепи показывает 0, можно замкнуть ключи К₁ и К₂ во вторичной цепи.

в) С помощью ЛАТРа постепенно увеличивая напряжение в первичной цепи последовательно установить значения тока I₂ от 2 А до 10 А через 2 А.

г) В табл. 46.2 занести показания амперметра и ваттметра (I₁ и P₁) в первичной цепи.

Таблица 46.1.

U1, В	I1, А	P1, Вт	U2, В	I2, А	P2, Вт
Режим холостого хода
1201	15	43	105	0	0
Рабочий режим
				1,0
				2,0
				…
				…
				10

Таблица 46.2.

Режим короткого замыкания.
I2, А	2,0	4,0	6,0	8,0	10,0
P1, Вт
I1, А

Содержание отчета

1. Таблицы наблюдений в режиме холостого хода, рабочем режиме и в режиме короткого замыкания.

2. Расчет коэффициента трансформации К из данных табл. 46.1 по формуле (46.3).

3. Величина потерь мощности в стальном сердечнике трансформатора, определенная из табл. 46.1.

4. Расчет значений КПД трансформатора в зависимости от тока во вторичной обмотке 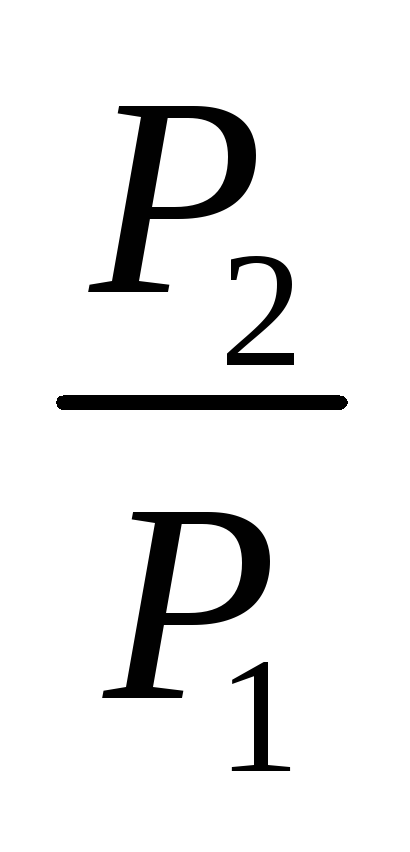 = = f(I₂). График зависимости  = f(I₂).

5. Вычисление значений cos₁ и cos₂ по формулам (46.7) и (46.9). Графики зависимости этих коэффициентов от тока I₂.

6. Расчет среднего значения активного сопротивления r из данных табл. 46.2 по формуле (46.10).

7. Расчет среднего значения коэффициента трансформации К из данных табл. 46.2 по формуле (46.11). Сравнение полученного значения с коэффициентом, рассчитанным по формуле (46.3).

8. График зависимости потерь мощности P_дж на нагревание в проводах обмоток от величины I₂ (P_дж = f(I₂)) (по указанию преподавателя).

9. Из построенного графика (P_дж = f(I₂)) найти то значение тока I₂, при котором P_ст = P_дж. Убедиться, что положение максимума КПД приходится на это значение тока.

Контрольные вопросы

• Какой физический закон лежит в основе работы трансформатора?

• Какие режимы работы трансформатора предлагается изучить в работе?

• Что такое коэффициент мощности трансформатора?

• В каком режиме можно определить коэффициент трансформации?

Лабораторная работа 47

РЕЗОНАНС НАПРЯЖЕНИЙ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА

Задачи работы

1. Построение векторных диаграмм напряжений.

2. Расчет полного, активного и реактивного сопротивлений.

3. Определение индуктивности и емкости цепи.

4. Расчет коэффициента перенапряжений.

Физическое обоснование эксперимента

Прежде чем приступить к изучению работы, необходимо ознакомиться с главой «Переменный ток».

Резонансом называется явление возбуждения колебаний большой амплитуды при частоте внешней возбуждающей силы, равной или близкой к собственной частоте колебательной системы.

Рассмотрим последовательную цепь, содержащую активное сопротивление R, индуктивность L и емкость С, на которые подается переменное напряжение U = U₀·sint (рис. 47.1).

Рис. 47.1.

Известно, что полное сопротивление (импеданс) такой цепи равно

,

где X_L = L – индуктивное сопротивление, а – емкостное сопротивление. Сдвиг фаз  между током I в такой цепи и внешним напряжением U выражается формулой

.

(47.1)

Сила тока в цепи определяется по закону Ома:

.

Если при определенных соотношениях между , L и C окажется, что

,

(47.2)

т.е. X_L = X_C, то сопротивление Z будет минимально:

,

и, следовательно, ток при данном напряжении на зажимах цепи будет иметь максимальное значение. Индуктивное напряжение U_L и емкостное U_C окажутся равными по величине, но сдвинутыми по фазе на 1/2 периода, а внешнее напряжение равно напряжению на активном сопротивлении U = U_R = I·R. Ток при этом по фазе совпадает с внешним напряжением, поскольку  = 0. Это явление носит название резонанса напряжений. Его иллюстрирует векторная диаграмма напряжений (рис. 47.2).

Рис. 47.2.

Условие резонанса выражено формулой (47.2). Оно выполняется при круговой частоте , где ₀ – собственная частота незатухающих колебаний колебательного контура, содержащего только L и C.

Если одновременно увеличить в n раз оба реактивных сопротивления, т.е. заменить X_L и X_C сопротивлениями X_L′ и X_C′:

X_L′ = n·X_L и X_C′ = n·X_C,

то сила тока в цепи не изменится, а падения напряжения на X_L′ и X_C′ возрастут в n раз и достигнут значений:

U_L′ = n·U_L и U_C′ = n·U_C.

Таким образом, можно безгранично увеличивать оба реактивных напряжения, а сила тока в цепи при этом останется неизменной:

I = U/R.

Практически предел повышению реактивных напряжений положит пробой изоляции между обкладками конденсатора или витками катушки.

При резонансе реактивная мощность равна нулю, полная мощность равна активной мощности, и коэффициент мощности cos = 1.

В электроэнергетических установках в большинстве случаев резонанс напряжений – явление нежелательное, связанное с возникновением напряжений, в несколько раз превышающих рабочее напряжение установки (перенапряжений). А в электротехнике связи явление резонанса напряжений широко используется для настройки цепи на определенную частоту.

Метод исследования и описание установки

Электрическая схема измерений представлена на рис. 47.3. В настоящей работе резонанс достигается изменением индуктивности L катушки, снабженной выдвижным железным сердечником, при постоянных круговой частоте  и емкости конденсатора C. Реальная катушка, кроме индуктивного сопротивления X_L, обладает также активным сопротивлением, но для изучения влияния на резонанс возрастания активного сопротивления в схему включен реостат R.

Рис. 47.3.

Источником переменной ЭДС служит вторичная обмотка понижающего трансформатора Тр. Во вторичную цепь последовательно включают катушку индуктивности L, реостат R, конденсатор C и амперметр A. Параллельно нагрузкам включают три вольтметра: V₀ – для измерения входного напряжения U₀; V₁ – для измерения падения напряжения на активно-индуктивной нагрузке U₁ и V₂ – для измерения падения напряжения на емкостной нагрузке U₂.

Порядок выполнения работы

1. Собрать электрическую схему (рис. 47.3).

2. Установить ползунковый реостат в первое положение (реостат полностью выведен).

3. При полностью вдвинутом в катушку сердечнике включить сеть. По вольтметру V₀ измерить подаваемое на схему напряжение U₀.

4. Постепенно выдвигая сердечник, добиться явления резонанса напряжений. При этом ток в цепи имеет максимальное значение (I)₃.

5. Записать показания всех приборов в табл. 47.1 на строку 3.

Таблица 47.1.

№ п/п	I, A	U0, В	U1, В	U2, В
	Первое положение реостата
1
…
5
	Второе положение реостата
1
...
5

6. Продолжая выдвигать сердечник, установить ток в цепи, равный I₂ и I₁ (по указанию преподавателя). Записать показания приборов в табл. 47.1 (строки 2 и 1).

7. Вернуть сердечник в положение, соответствующее резонансу.

8. Продолжая вдвигать сердечник, установить ток в цепи, равный I₄ и I₅ (по указанию преподавателя). Записать данные в строки 4 и 5 табл. 47.1.

9. Повторить измерения пунктов 4 – 8 при другом положении движка реостата (реостат введен на 1/5 всей длины) и занести данные в табл. 47.1 (по указанию преподавателя).

Обработка результатов измерений

1. По полученным данным на миллиметровой бумаге построить векторные диаграммы напряжений (рис. 47.4).

Рис. 47.4.

За исходный принимается вектор тока I. От его начала откладывают вектор U₂ падения напряжения на емкости, который отстает от вектора тока на угол . Затем в выбранном масштабе циркулем делают засечку из начала координат радиусом, равным U₀, а из конца вектора U₂ – радиусом, равным U₁. Пересечение этих двух засечек дает третью вершину векторного треугольника напряжений (см. рис. 47.4,a):

U₀ = U₁ + U₂.

Угол  сдвига фаз между вектором тока I и вектором внешнего напряжения U₀ определяется транспортиром. Затем вектор U₁ переносится параллельно самому себе так, чтобы его начало совпало с началом координат, и транспортиром определяется угол ₁ сдвига фаз между I и вектором U₁ падения напряжения на активно-индуктивной нагрузке (рис. 47.4,b).

Затем вектор U₁ раскладывается на два: вектор U_L падения напряжения на чисто индуктивной нагрузке, опережающий по фазе вектор I на угол , и вектор U_R падения напряжения на активной нагрузке, совпадающий по фазе с I. Вектор U_R включает в себя падение напряжения на активной составляющей импеданса катушки и на реостате.

Примечания:

а) еще раз напомним, что при построении диаграмм необходим единый масштаб для U₀, U₁ и U₂;

б) поскольку U₀ в ходе работы не изменяется, то все векторные диаграммы можно, в принципе, привести на одной схеме.

2. Построить векторные диаграммы напряжений для использованных в работе параметров электрической цепи.

3. Из векторных диаграмм определить углы  и ₁.

4. Полное Z, активное R и реактивное X сопротивления определить по формулам

Z = U₀/I;

R = Z·cos;

Х = Z·sin.

5. Индуктивную U_L и активную U_R составляющие напряжения U₀ определить из векторных диаграмм по проекциям на оси. Емкостная составляющая U_C = U₂.

6. Индуктивную, емкостную и активную составляющие полного сопротивления (импеданса) найти по формулам:

X_L = U_L/I;

X_C = U_C/I;

R = U_R/I.

Сравнить R и Х = X_L – X_C со значениями, полученными в п.4.

7. Индуктивность цепи в каждом опыте и емкость цепи (постоянную в данной работе величину) найти по формулам:

;

,

где  = 2·f – круговая частота, f = 50 Гц – частота переменного тока.

8. Определить угол сдвига фаз между I и U₀ по формуле (47.1) для разных опытов и сравнить это значение со значением  из п. 3 (по указанию преподавателя).

9. Рассчитать резонансную частоту по формуле:

.

10. Рассчитать коэффициент перенапряжений в случае резонанса по формуле:

    .

11. Построить графики функциональных зависимостей I₀ = f(L), U_L = f(L), U_C = f(L).

Определение погрешностей измерений

Погрешности измеренных величин I, U₀, U₁ и U₂ определяются по классам точности соответствующих приборов. Погрешности вычисляемых величин определяются по формулам переноса ошибок (см. методические указания «Математическая обработка результатов измерений») и рассчитываются по указанию преподавателя. Кроме того, графический метод векторных диаграмм вносит дополнительную погрешность. Для ее уменьшения необходимо строить диаграммы в возможно большем масштабе.

Если в работе используются одинаковые по точности вольтметры V₁ и V₂, то, методом переноса ошибок, получаем упрощенную формулу для погрешности резонансной частоты

.

Содержание отчета

1. Электрическая схема измерений.

2. Табл. 47.1 с результатами измерений.

3. Векторные диаграммы для всех случаев и определенные по ним углы  и ₁ и напряжения U_R и U_L.

4. Табл. 47.2 с рассчитанными в работе величинами. При ее заполнении пункты с 1-го по 5-й должны соответствовать пунктам табл. 47.1.

Таблица 47.2.

№ п/п		1	Z, Ом	r, Ом	X, Ом	UC, В	UL, В	UR, В	XL, Ом	XC, Ом	L, Гн	C, мкФ	cos	sin	cos1
	Первое положение реостата
1
...
5
	Второе положение реостата
1
...
5

5. Графики зависимостей: I = f(L), U_L = f(L), U_C = f(L) для двух положений реостата.

6. Расчет k, f и f для резонанса.

7. Объясните полученные графики функциональных зависимостей.

Контрольный вопрос

• Как можно увеличить коэффициент мощности cos в электрических цепях?

Лабораторная работа 48

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА И ПОСТРОЕНИЕ ТРЕУГОЛЬНИКОВ МОЩНОСТЕЙ

Задачи работы

1. Определение коэффициента мощности, а также других параметров цепи переменного тока с помощью расчетов и векторных диаграмм для различных нагрузок.

2. Построение треугольников мощностей.

Физическое обоснование эксперимента

Прежде чем приступить к выполнению работы, необходимо ознакомиться с главами «Переменный электрический ток», «Построение векторных диаграмм», «Мощность переменного тока».

Метод исследования и описание установки

Электрическая схема для измерений изображена на рис. 48.1. В нее входят: источник питания – лабораторный автотрансформатор (ЛАТР), вольтметр V, амперметр А, ваттметр W и нагрузка Z. В качестве нагрузки используются различные комбинации омического сопротивления R, индуктивности L и емкости С.

Р

ис. 48.1.

Автотрансформатор представляет собой трансформатор, у которого вторичной обмоткой служит часть первичной обмотки. У лабораторного автотрансформатора число витков вторичной обмотки может плавно регулироваться путем перемещения подвижного контакта по обмотке. Это дает возможность регулировать напряжение в данной лабораторной работе от 0 до 127 В.

ВНИМАНИЕ! В автотрансформаторе имеется прямое электрическое соединение вторичной и первичной обмоток. Поэтому даже при низком выходном напряжении прикосновение к оголенным частям схемы опасно! В связи с этим при замене нагрузки, а также по окончании работы необходимо вывести до нуля выходное напряжение ЛАТРа и выключить его из сети!

Ваттметр имеет две катушки: «токовую», включаемую, как амперметр, последовательно измеряемому объекту и «вольтовую», которая подсоединяется параллельно объекту измерения, как вольтметр (подробнее об устройстве и принципе действия ваттметра см. «Ваттметр»). Начало каждой обмотки отмечено звездочкой. Эти клеммы необходимо присоединить к одному полюсу источника. В таком случае токи в обеих обмотках будут течь в одном и том же направлении, что обеспечит отклонение стрелки прибора в нужную сторону. Для простоты отмеченные звездочкой клеммы закорачивают (соединяют друг с другом), поэтому к полюсу источника достаточно присоединить только одну из них.

Используемый в данной работе ваттметр имеет раздельные переключатели пределов измерения для токовой и вольтовой обмоток. Номинальное значение по мощности (предел измерения в ваттах) равно произведению пределов измерения по току в амперах и напряжению в вольтах.

Постановка задачи

Схема, представленная на рис. 48.1, дает возможность измерить активную мощность Р и действующие значения тока I и напряжения U на нагрузке Z. Это позволяет рассчитать ряд величин:

а) Полную мощность S = U·I,

б) Коэффициент мощности cos = P/S,

в) Реактивную мощность ,

г) Импеданс Z, для определения которого следует применить обобщенный закон Ома Z = U₀/I₀, перейдя от амплитуд I₀, U₀ к действующим значениям тока и напряжения,

д) Активное сопротивление нагрузки r

Р

ис. 48.2.

Из векторной диаграммы напряжений (рис. 48.2), представляющей собой прямоугольный треугольник, катеты которого равны действующим значениям падений напряжения на активном и реактивном сопротивлениях U_r и U_x, а угол  совпадает со сдвигом фаз между общим напряжением U, подаваемым в цепь, и током, имеем следующее:

Ur = U cos.

(48.1)

Тогда выражение для активной мощности может быть преобразовано таким образом:

P = I·U·cos = I·Ur.

(48.2)

Учитывая, что по закону Ома U_r = I·r, то из (48.2) нетрудно получить формулу, связывающую между собой величины P, I и r, откуда и выразить активное сопротивление нагрузки r.

Примечание. Активным сопротивлением обладает не только омическое сопротивление R, но также катушка и конденсатор. Активное сопротивление катушки обусловлено омическим сопротивлением ее обмотки, активное сопротивление конденсатора связано с потерями в диэлектрике. Определяемое активное сопротивление нагрузки r равно сумме активных сопротивлений всех элементов, составляющих данную нагрузку, а также соединительных проводов.

Реактивное сопротивление нагрузки:

.

Запишем выражение для импеданса в виде

.

(48.3)

Для определения Х из формулы (48.3) достаточно воспользоваться вычисленными ранее значениями Z и r.

Индуктивность катушки L и емкость конденсатора С:

Найдя реактивное сопротивление нагрузки, учтем, что оно равно:

X = ·L	в случае, если в качестве нагрузки выбрана катушка индуктивности или комбинация омического сопротивления R и катушки;
	в случае, если в качестве нагрузки выбран конденсатор или комбинация омического сопротивления R и конденсатора.

Значение круговой частоты определяется по формуле:  = 2·f, где f – частота тока в герцах (f = 50 Гц).

На рис. 48.3 показаны различные виды нагрузок, с которыми следует произвести измерения в работе.

Рис. 48.3.

В качестве нагрузки VIII используется катушка индуктивности, в которую поэтапно вводится сердечник из ферромагнитного материала. При каждом измерении сердечник постепенно вдвигают в катушку на 1/5 всей его длины. Индуктивность катушки при этом будет возрастать. Увеличиваться начнут и потери мощности при измерениях из-за возникновения токов Фуко в сердечнике. Нагревание сердечника и катушки проявляется в увеличении активного сопротивления катушки. Расчеты производятся для всех 5 положений вдвигаемого в катушку сердечника. По этой части работы необходимо построить график зависимости cos от L. (Как он должен выглядеть и почему?)

а	б
Рис. 48.4.

Для нагрузок II  VII требуется построить треугольник напряжений (рис. 48.4,а). В выбранном масштабе на горизонтальной оси следует отложить активное напряжение, вычисляемое по формуле U_r = P/I, которая следует из (48.2). Затем из точки O радиусом, равным величине общего напряжения U, поданного в цепь, проводим дугу. Из конца вектора U_r (точка А) восстанавливаем перпендикуляр до пересечения с дугой (точка В). Катет АВ дает в масштабе падение напряжения на реактивном сопротивлении U_Х, что позволяет определить реактивное сопротивление Х вторым способом – графическим, воспользовавшись соотношением Х = U_X/I. Графически можно также получить значение коэффициента мощности (cos), измерив угол АOВ транспортиром.

Если все стороны треугольника напряжений умножить на величину общего тока I, получится треугольник мощностей (не векторный) (рис. 48.4,б). Таким образом, графическое получение величин полной S и реактивной Q мощностей сводится к построению треугольника, подобного треугольнику АOВ. (Строим угол , на одном луче которого откладываем в масштабе активную мощность Р и восстанавливаем перпендикуляр до пересечения с другим лучом.)

Примечание. Вначале следует построить векторные диаграммы для нагрузок II и III (или IV и V). При этом необходимо учесть, что векторы напряжения на индуктивности U_X = U_L и емкости U_X = U_С образуют с вектором U_r углы /2 и –/2, соответственно. Поэтому их нужно откладывать в противоположных направлениях (рис. 48.5). В случае нагрузок VI и VII вектор U_X, длина которого дает общее напряжение на катушке и конденсаторе, следует направить в ту же сторону, что и более длинный из векторов U_L и U_C, построенных ранее (объясните почему). Диаграммы мощностей строятся в соответствии с тем, что условно принято считать Q_L  0, а Q_С  0 (рис. 48.5).

Р

ис. 48.5.

Порядок выполнения работы

1. Собрать электрическую схему (см. рис. 48.1).

Сначала соединяют все элементы схемы, включаемые последовательно, начиная с одного из зажимов источника тока (ЛАТР); последний провод подсоединяют ко второму полюсу источника. (У ваттметра на этом этапе подключаются токовые клеммы, причем клемма, помеченная звездочкой, подсоединяется к источнику). Затем подключают вольтметр и вольтовую обмотку ваттметра параллельно нагрузке. (Фактически подсоединяется только не помеченная звездочкой клемма вольтовой обмотки, так как «звездочка», закороченная с токовой обмоткой, уже подключена). К каждой клемме нагрузки следует присоединять не более одного провода. Все параллельные подключения целесообразно выполнять на клеммах приборов (ЛАТР, амперметр, ваттметр). Это облегчит смену нагрузки, поскольку в таком случае понадобится отсоединять меньшее число проводов.

2. Измерить величины P, U, I для различных нагрузок.

Начинать необходимо с первой нагрузки – омического сопротивления, при этом произведение тока на напряжение должно быть равно мощности, определяемой по ваттметру (Почему?). Этим проверяется правильность расчета цены деления каждого прибора.

Все измерения производятся однократно, при токе в цепи I = 2 А для нагрузок I – VII и при максимально возможном токе для нагрузки VIII. Величина тока, зависящая от подаваемого в цепь напряжения, регулируется ЛАТРом.

Снятые показания представить в виде таблицы.

3. Получить формулы для расчета cos, S, Q, Z, r, X, L и С.

4. Произвести вычисления по этим формулам для нагрузок I – VIII (нагрузка VIII – пять положений). Подумайте, все ли перечисленные величины можно найти для каждой конкретной нагрузки и почему.

5. Для нагрузок II – VII определить величины cos, S, Q, Х графически. Сравнить их с расчетными.

Результаты вычислений привести в таблице (расч – расчетные значения, граф – определенные графически, L₁ – L₅ – пять положений катушки с сердечником).

Таблица 48.1.

Нагрузка	cos		S		Q		Z	r	X		L	C
	Расч	Граф	Расч	Граф	Расч	Граф	Расч	Расч	Расч	Граф	Расч	Расч
I: R
II: L
III: C
IV: RC
V: RL
VI: LC
VII: RLC
VIII: L1
VIII: L2
VIII: L3
VIII: L4
VIII: L5

6. Построить график зависимости cos от L.

7. Рассчитать погрешность r в случае нагрузки 1 и коэффициента мощности в случае нагрузок 2 – 7, для чего записать класс точности всех приборов, а также номинальные значения P, U, I (см. «Определение погрешности измерения на ЭИП. Класс точности прибора.»).

Расчет погрешностей измерений

1. Погрешности при прямых измерениях (т.е. погрешности измерения P, I, U) определяются по классу точности измерительных приборов.

2. Величины r и cos вычисляются как функции от U, I и P, U, I соответственно. Поэтому r и cos представляют собой погрешности косвенных измерений (см. методические указания «Математическая обработка результатов измерений»). Для их расчета удобно воспользоваться формулой относительной погрешности произведения (частного).

Содержание отчета

1. Формулы для расчета cos, S, Q, Z, r, X, L и C, а также R и cos.

2. Результаты измерений и вычислений, записанные в таблицах.

3. Векторные диаграммы напряжений и треугольники мощностей для нагрузок 2-7.

4. График зависимости cos от L для нагрузок 8.1-8.5.

5. Величины r (для нагрузки 1) и cos (для нагрузок 2-7) с погрешностями.

Контрольные вопросы

• Можно ли определить сдвиг фаз между током и напряжением в цепи, имеющей индуктивную или емкостную нагрузку, если известен коэффициент мощности?

• Как будет изменяться коэффициент мощности в цепи переменного тока при увеличении омического сопротивления в этой цепи?

Лабораторная работа 50

ИЗУЧЕНИЕ СВОЙСТВ ФЕРРОМАГНИТНЫХ ВЕЩЕСТВ С ПОМОЩЬЮ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА

Физическое обоснование эксперимента

Ферромагнетиками называют вещества, обладающие в определенном температурном диапазоне особыми свойствами:

• сильное намагничивание в магнитном поле;

• сохранение намагниченного состояния при отсутствии внешнего магнитного поля;

• нелинейная зависимость магнитной проницаемости и магнитной индукции от напряженности магнитного поля.

Эти особые свойства ферромагнетиков нашли объяснение в квантовой теории. У ферромагнитных веществ имеются неспаренные (ответственные за ферромагнетизм) электроны, спины которых в сравнительно больших областях ориентируются в одном направлении. Каждая из таких областей или, как их обычно называют, доменов, намагничена до насыщения. Разные состояния намагниченности всего образца отличаются взаимной ориентацией векторов намагниченности отдельных доменов: в размагниченном веществе они расположены хаотически, а в намагниченном направлены в одну сторону.

Магнитная индукция B и напряженность магнитного поля H связаны в системе СИ соотношением:

B = 0··H,

(50.1)

где ₀ – магнитная постоянная,  – магнитная проницаемость среды.

Если размагниченный ферромагнитный образец поместить во внешнее магнитное поле Н и произвести полный цикл перемагничивания (т.е. изменить напряженность магнитного поля от 0 до Н, затем до Н и от Н до Н), то значения магнитной индукции B будут изменяться по кривой, называемой петлей гистерезиса (рис. 50.1).

Кривая 0А – основная кривая намагничивания. Отрезок 0Д определяет величину остаточной индукции В_ост в образце (при Н = 0). Изменив направление напряженности магнитного поля, можно снять остаточную индукцию в образце. Отрезок 0С определяет то значение напряженности магнитного поля Н_К, при котором индукция в образце равна нулю. Величина напряженности Н_К называется коэрцитивной силой.

Рис. 50.1.

Для изготовления постоянных магнитов применяют магнитные вещества с большим остаточным намагничиванием и большой коэрцитивной силой (жесткие стали). Для изготовления сердечников трансформаторов применяют мягкие магнитные материалы с малым остаточным намагничиванием и малой коэрцитивной силой.

Метод исследования и описание установки

Данная работа заключается в исследовании кривой гистерезиса ферромагнитного образца на экране электронного осциллографа. Электрическая схема состоит из лабораторного автотрансформатора (ЛАТР 1) в первичной цепи, резистора R₁, намагничивающей катушки L₁, намотанной на рамку (образец K), вторичной измерительной катушки L₂ на том же образце, резистора R₂, конденсатора С. Электрическая схема установки (рис. 50.2) собрана постоянно в специальном корпусе.

Рис. 50.2.

Чтобы получить петлю гистерезиса на экране осциллографа, необходимо по намагничивающей катушке L₁ пропустить переменный намагничивающий ток I₁. Проходя по сопротивлению, включенному в первичную цепь, ток создает падение напряжения U_X на резисторе R₁, которое подается на усилитель горизонтально отклоняющих пластин электронно-лучевой трубки. Ток I₁ в намагничивающей катушке L₁, будет пропорционален напряженности магнитного поля Н. На вертикально отклоняющие пластины осциллографа подается напряжение, пропорциональное индукции поля В в образце K (вход Y). Тогда за один период изменения синусоидального тока в катушке L₁ электронный луч на экране опишет гистерезисную петлю, а каждый последующий период повторит ее.

Если ток I₁ постепенно уменьшать, то каждому значению тока I₁, будет соответствовать своя петля гистерезиса (частные циклы) – см. рис. 50.3,а (1 – полный цикл; 2 – частный цикл).

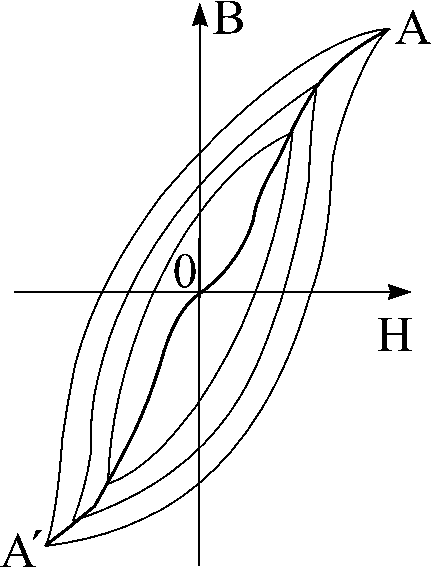
а б

Рис. 50.3.

Вершины всех петель гистерезиса будут лежать на основной кривой намагничивания (рис. 50.3, б).

Напряжение U_x снимается с резистора R₁, соединенного последовательно с катушкой L₁ в намагничивающей цепи. Ток в намагничивающей цепи:

.

(50.2)

Напряженность магнитного поля в образце:

,

(50.3)

где N₁ и l₁ – число витков и длина намагничивающей катушки. Для одного витка катушки l₁ = 2·r, где r – радиус катушки. Подставим (50.2) в (50.3):

.

(50.4)

Из формулы (50.4) видно, что напряженность магнитного поля пропорциональна падению напряжения U_X на резисторе R₁.

На вертикально отклоняющие пластины подается напряжение U_Y, снимаемое с конденсатора С, которое будет пропорционально индукции магнитного поля.

ЭДС, возникающая при изменении магнитного потока Ф в катушке, охватывающей образец, равна

.

(50.5)

Пусть катушка плотно охватывает образец, и индукция В в образце однородна. В этом случае

Ф = S·N2·B,

(50.6)

где N₂ – число витков в обмотке L₂, а S – площадь витка. Подставим (50.6) в (50.5):

(50.7)

или

E·dt = –d(S·N2·B).

После интегрирования этого выражения мы получаем:

.

(50.8)

Таким образом, для определения В нужно проинтегрировать сигнал, наведенный в обмотке L₂ меняющимся магнитным полем первичной катушки. Для интегрирования сигнала применяют разного рода интегрирующие схемы. Простейшая из них состоит из соединенных последовательно резистора и конденсатора, и называется RC-цепоч кой (рис. 50.4). Она выполняет свое назначение, если выходной сигнал значительно меньше входного: U_вых << U_вх.

Рис. 50.4.

В самом деле, при выполнении этого условия I₂ = U_вх/R₂ и

.

(50.9)

Мы видим, что выходной сигнал R₂C цепочки действительно пропорционален интегралу от входного сигнала. Этот вывод тем ближе к истине, чем больше постоянная времени цепочки R₂C превосходит характерное время процесса, например, его период. Так как

,

то, подставляя это в (50.9), получаем

.

(50.10)

В формуле (50.10) N₂ – число витков катушки L₂, S – площадь поперечного сечения сердечника образца K.

В описываемой установке R₁ = 0,28 Ом, R₂ = 513 кОм, С = 1мкФ. В данной работе используется электронный осциллограф С1-83, в котором определенное отклонение луча трубки по оси X и по оси Y сразу можно установить регулятором чувствительности отклонения луча по экрану (В/см). Но указанное на осциллографе напряжение дается в амплитудном значении этой величины. Для использования в дальнейшем этой чувствительности необходимо ее перевести в действующее или эффективное значение напряжения, т.е. разделить на .

Таким образом, в этой работе специальной градуировки отклонения луча осциллографической трубки по напряжению не требуется.

Порядок выполнения работы

Электрическая схема работы (см. рис. 50.2) собрана постоянно в специальном корпусе, на верхней крышке которого имеется ее изображение со всеми параметрами. Внутри корпуса находятся 4 изучаемых ферромагнитных образца, которые могут последовательно подключаться к схеме с помощью специального переключателя.

Рис. 50.5.

Вход усилителя X-пластин осциллографа С1-83 включается параллельно резистору R₁, включенному последовательно с катушкой намагничивания L₁ образца. Вход усилителя Y-пластин включается параллельно конденсатору C интегрирующей цепочки.

Передняя панель осциллографа С1-83 схематически представлена на рис. 50.5.

В начале работы необходимо включить осциллограф кнопкой 8 (питание), вытянув эту кнопку на себя (слева от кнопки загорится сигнальная лампочка). Дать прогреться осциллографу 3–5 минут. После чего сфокусировать электронный луч на экране трубки регулятором 9 (Яркость) и регулятором 10 (Фокусировка). При этом нельзя получать на экране очень интенсивное светлое пятно, так как можно прожечь люминофор экрана трубки. Вывести луч на центр экрана трубки при помощи вытянутого на себя регулятора 4 и утопленного регулятора 12. Затем нажать квадратные кнопки 6 и 7 (X–Y).

Регуляторы каналов I(X) и II(Y) (переключатели 1 и 3) в криволинейной прорези установить на переменный ток (~). Чувствительность канала I(X): большую ручку поставить на деление 50 mV, а малую ручку – до упора вправо. При этом кнопка переключателя 2 должна быть утоплена (×10).

Отрегулировать чувствительность канала II(Y) (переключатель 3): большую ручку установить в положение 1 mV, а малую рукоятку до упора вправо. Множитель чувствительности (регулятор 4) должен быть вытащен на себя до упора (×1).

Переключателем на крышке коробки включить образец 1. Затем включить ЛАТР 1 в сеть 220 В и получить гистерезисную кривую на экране осциллографа, увеличивая снимаемое напряжение с ЛАТР 1 таким образом, чтобы по оси X отклонение луча было бы приблизительно равно 8 большим делениям экрана. Если гистерезисная кривая будет иметь вид зеркального отражения нормальной кривой, то необходимо переключить полярность исходной цепи переключателем 5 (нажать его или вытянуть). Включить поворотом вправо регулятора II подсветку экрана осциллографа.

Приложить к экрану осциллографа лист кальки размером 12,5×10,5 см с заранее начерченной на ней сеткой, имеющейся на экране (размер квадрата 12×12 мм), и перевести карандашом гистерезисную кривую на кальку. Затем, уменьшая напряжение на схеме ЛАТР 1, зарисовать ход вершин гистерезисной кривой при уменьшении напряжения до нуля. Это и будет основная кривая намагничивания данного образца.

Выполнить аналогичную работу для следующих трех образцов, имеющихся в данной коробке. Перед переключением образцов необходимо выводить ЛАТР 1 на нулевое напряжение.

На полученных гистерезисных кривых образцов необходимо рассчитать масштабы по осям X и Y, т.е. по оси абсцисс необходимо оценить величину напряженности магнитного поля Н, соответствующую максимальному отклонению луча, а по оси ординат оценить максимальную индукцию магнитного поля в образце.

Максимальное значение напряженности магнитного поля Н в образце определяется по формуле

,

где U_X – двойное амплитудное значение максимального падения напряжения на резисторе R₁, которое равно

UX = mX·nX,

где m_X – чувствительность отклонения луча по оси X в В/дел, а n_X – число делений сетки шкалы, соответствующее максимальному отклонению луча. Тогда

(А·м-1) (в системе СИ),

(50.12)

где N₁ – число витков первичной обмотки L₁, l₁ – длина этой обмотки в метрах, R₁ – ее сопротивление (R₁ = 0,28 Ом).

Максимальное значение индукции магнитного поля В в образце определяется по формуле

(Тл),

(50.13)

где S – площадь поперечного сечения образца K в м², N₂ – число витков вторичной обмотки L₂, R₂ = 5,13·10⁵ Ом, С = 1·10^-6 Ф, m_Y – чувствительность отклонения электронного луча по оси Y в В/дел, n_Y – число делений сетки шкалы, соответствующее максимальному отклонению луча по оси Y (двойному амплитудному значению напряжения).

Для максимального значения индукции магнитного поля В для данного образца находим соответствующую величину магнитной проницаемости образца по формуле

,

(50.14)

где ₀ – магнитная постоянная, ₀ = 4·10^-7 Гн/м.

Содержание отчета

1. Электрическая схема установки.

2. Максимальное амплитудное значение напряжения, подаваемое по оси X, U_X = m_Xn_X для каждого данного образца.

3. Максимальное амплитудное значение напряжения, подаваемое по оси Y U_Y = m_Yn_Y для каждого данного образца.

4. Максимальное значение напряженности магнитного поля Н и индукции магнитного поля В для каждого исследованного образца.

5. Значение максимальной величины магнитной проницаемости для всех образцов.

6. Основная кривая намагничивания для всех исследуемых образцов.

7. Формы кривых гистерезиса для всех изученных образцов в рассчитанных масштабах.

Данные ферромагнитных образцов в работе №1

Образец № 1:	l1 = 3,3·10-2 м	S1 = 1,36·10-4 м2	N1 = 96	N2 = 7
Образец № 2:	l2 = 4,0·10-3 м	S2 = 0,72·10-4 м2	N1 = 1	N2 = 140
Образец № 3:	l3 = 7,8·10-4 м	S3 = 3,90·10-4 м2	N1 = 200	N2 = 14
Образец № 4:	l4 = 2,4·10-2 м	S4 = 1,19·10-4 м2	N1 = 44	N2 = 8

Данные ферромагнитных образцов в работе №2

Образец № 1:	l1 = 2,4·10-2 м	S1 = 0,39·10-4 м2	N1 = 25	N2 = 50
Образец № 2:	l2 = 8,0·10-2 м	S2 = 0,4·10-5 м2	N1 = 210	N2=1060
Образец № 3:	l3 = 6,3·10-2 м	S3 = 0,18·10-4 м2	N1 = 40	N2 = 180
Образец № 4:	l4 = 2,5·10-2 м	S4 = 1,12·10-4 м2	N1 = 25	N2 = 15

Контрольные вопросы

• В чем заключается основное отличие ферромагнитных веществ от диамагнитных и парамагнитных?

• Чем объясняются особые свойства ферромагнитных веществ?

• В каких единицах измеряется В в системах СГСМ, Гауссовой и СИ? Какое соотношение между этими единицами?

• Какое соотношение между эрстедом и единицей напряженности магнитного поля в системе СИ?

ПРИЛОЖЕНИЯ

Аналоговые электроизмерительные приборы

Аналоговые ЭИП представляют собой важнейшую группу приборов для электрических измерений. Они отличаются относительной простотой, дешевизной, высокой надежностью, разнообразием применения. Аналоговые приборы выпускаются разных классов точности.

Любой аналоговый ЭИП состоит из измерительной цепи и измерительного механизма. Измерительная цепь служит для преобразования измеряемой величины в другую, непосредственно воздействующую на измерительный механизм. Измерительная цепь может быть весьма сложной и служить также для усиления слабого измеряемого сигнала, как, например, в электрометрических усилителях, предназначенных для измерения слабых токов (< 10^-9 А).

Измерительный механизм состоит из подвижной и неподвижной частей и служит для преобразования подводимой электрической энергии в механическую энергию перемещения подвижной части. Принцип действия стрелочных измерительных приборов независимо от их назначения сводится к следующему: электрический ток, проходя через прибор, вызывает появление вращающего момента, под воздействием которого преодолевается противодействие спиральных пружин. Если бы спиральных пружин не было, то подвижная часть при любом значении измеряемой величины поворачивалась бы до упора. Для того чтобы угол поворота подвижной части зависел от измеряемой величины, с помощью спиральных пружин создается противодействующий момент. Подвижная часть поворачивается на определенный угол, при этом указатель, переместившись по шкале, показывает измеряемую величину. Когда прибор отключается, вращающий момент исчезает, и подвижная часть, вследствие упругости пружин, возвращается в исходное положение.

При изменении температуры окружающей среды упругость пружин меняется, что приводит к некоторому повороту подвижной части. Перед началом измерений стрелка прибора должна располагаться против нулевого деления шкалы. Установку стрелки на ноль производят с помощью корректора.

Подвижная система прибора должна быстро успокаиваться, что обеспечивается применением воздушных, жидкостных или магнитных успокоителей (демпферов).

Каждый прибор снабжен отсчетным устройством, состоящим из шкалы и указателя. В качестве указателя используется стрелка или световой луч. Использование светового луча значительно увеличивает чувствительность прибора. В приборах высокой чувствительности имеется арретир – устройство, закрепляющее подвижную часть.

Аналоговые измерительные приборы различаются:

а) По назначению.

Приборы подразделяются на амперметры (А), вольтметры (V), омметры (R), ваттметры (W), частотомеры и др. В скобках приведены значки, которые обычно нанесены на шкале соответствующего измерительного прибора.

б) По роду измеряемого тока.

Многие измерительные приборы можно применять в цепях только постоянного (–) или только переменного (~) тока. Однако существуют приборы, которые могут быть включены как в цепь постоянного, так и в цепь переменного тока.

в) По принципу действия.

По принципу действия приборы ЭИП относят к следующим наиболее распространенным системам:

Электромагнитной Магнитоэлектрической Электродинамической Индукционной Электростатической Вибрационной

г) По степени точности.

По степени точности ЭИП делятся на 8 классов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5, 4,0 (цифры указывают основную погрешность прибора в процентах). Приборы классов точности 0,05 и 0,1 называются контрольными, 0,2 и 0,5 – лабораторными, 1,0; 1,5 и 2,5 – техническими, 4,0 – учебными. Контрольные приборы имеют зеркальную шкалу и ножевидную стрелку. У лабораторных приборов имеется ножевидная стрелка, но может не быть зеркальной шкалы. Технические и учебные приборы не имеют зеркальной шкалы, и стрелка у таких приборов имеет копьевидную форму.

Зеркальная шкала обеспечивает высокую точность снятия показаний. При определении показаний приборов, имеющих зеркальную шкалу, глаз наблюдателя должен быть расположен так, чтобы стрелка закрывала свое изображение в зеркале.

д) По положению при измерениях.

Приборы делятся на вертикальные (), горизонтальные (—) и устанавливаемые под углом ().

е) По характеру применения.

Выпускаются электроизмерительные приборы трех эксплуатационных групп: А, Б, В. Буквы характеризуют допустимую температуру окружающей среды, при которой их можно использовать.

А:	от	0 °С	до	+35 °С
Б:	от	–30 °С	до	+40 °С
В:	от	–50 °С	до	+60 °С

Принадлежность к эксплуатационным группам Б и В обычно указывается на шкале. Приборы группы А обозначений на шкале обычно не имеют.

На шкале измерительных приборов условными значками и цифрами указываются следующие данные: назначение, род тока, система прибора, напряжение, при котором испытана изоляция, положение при измерениях, класс точности, а также год выпуска, номер прибора и его принадлежность к эксплуатационной группе.

Значки на шкале прибора позволяют дать полную техническую характеристику ЭИП. ЭИП, шкала которого приведена на рис. 26, представляет собой вольтметр электромагнитной системы для измерения переменного напряжения в пределах от 0 до 150 В. При измерениях прибор должен быть расположен вертикально. Класс точности 1,0; изоляция прибора испытана при 2 кВ; эксплуатационная группа Б (от –30 °C до +40 °C); год выпуска 1995; заводской номер 2132.

Рис. 26.

Краткая характеристика электроизмерительных приборов наиболее распространенных систем

1. Приборы электромагнитной системы применяются для измерения как постоянного, так и переменного тока и напряжения.

Достоинства – простота, дешевизна, надежность, способность выдерживать кратковременные перегрузки.

Недостатки – сравнительно малая точность (класс точности 1,0; 1,5; 2,5), неравномерность шкалы, довольно большая потребляемая мощность, зависимость показаний от частоты тока и влияния внешних магнитных полей.

2. Приборы магнитоэлектрической системы применяются для измерений тока и напряжения только в цепях постоянного тока. Приборы полярны – имеют положительный и отрицательный зажимы (клеммы). В цепях переменного тока не дают показаний.

Достоинства – высокая точность, большая чувствительность, равномерная шкала, малое потребление энергии, быстрое успокоение подвижной системы, малая чувствительность к внешним магнитным полям. Приборы магнитоэлектрической системы самые точные и чувствительные приборы постоянного тока.

Недостатки – чувствительность к перегрузкам, сравнительно высокая стоимость.

3. Приборы электродинамической системы применяются для измерения силы тока, электрического напряжения, мощности и т.д. в цепях переменного и постоянного тока. Работа приборов основана на взаимодействии магнитных полей подвижной и неподвижной катушек с токами.

Достоинства – высокая точность. Самые точные приборы переменного тока. Шкала, начиная с 20% номинального значения почти равномерная.

Недостатки – большое собственное потребление мощности при измерении токов и напряжений, чувствительность к внешним магнитным полям и перегрузкам, высокая стоимость.

4. Приборы индукционной системы применяются для измерения расхода электрической энергии в цепях переменного тока (электрические счетчики).

Достоинства – нечувствительность к внешним магнитным полям, способность выдерживать значительные перегрузки.

Недостатки – пригодны только для переменного тока, низкая точность, чувствительность к колебаниям частоты.

5. Приборы вибрационной системы предназначены для измерения частоты переменного тока.

Достоинства – независимость показаний от напряжения сети.

Недостатки – зависимость показаний от механических вибраций, невозможность измерения высоких частот.

Измерительные трансформаторы тока и напряжения

Измерительные трансформаторы тока и напряжения используются в цепях переменного тока для расширения пределов измерения ЭИП и для изоляции этих приборов от токопроводящих частей, находящихся под высоким напряжением. Измерительные трансформаторы преобразуют большие переменные токи и напряжения в относительно малые токи и напряжения, допустимые для измерения приборами с небольшими пределами измерения.

Трансформаторы напряжения представляют собой обычные трансформаторы малой мощности. Коэффициент трансформации трансформатора выбирается таким, чтобы при номинальном первичном напряжении напряжение вторичной обмотки было 100 В. Первичная обмотка трансформатора напряжения включается в два линейных провода сети, а во вторичную обмотку включается вольтметр или «вольтовая» обмотка ваттметра.

Рис. 27.

Трансформаторы тока служат для преобразования переменного тока и изготавливаются так, чтобы при номинальном токе в первичной обмотке ток во вторичной обмотке был 5 А. Первичная обмотка трансформатора включается в разрыв линейного провода последовательно с нагрузкой, ток которой измеряется, во вторичную обмотку включается амперметр или «токовая» обмотка ваттметра. Режим работы трансформатора тока близок к режиму короткого замыкания (подробнее о режиме короткого замыкания – см. работу 46). На рис. 27 показаны условные обозначения трансформаторов тока (Б) и напряжения (А).

ПОСТРОЕНИЕ ВЕКТОРНЫХ ДИАГРАММ

При сложении колебаний типа x = A·sin(ωt + φ) удобно каждое из них представлять в виде радиус-вектора А, вращающегося во времени с угловой скоростью  против часовой стрелки. Тогда проекция вектора А на ось Y будет соответствовать написанному виду колебаний. При t = 0 вектор А составит с осью X угол . Это начальная фаза колебаний.

Поскольку взаимная ориентация векторов сохраняется в любой момент времени (т.е. не зависит от времени), то для построения векторных диаграмм токов и напряжений достаточно указать их фазовые углы в момент t = 0. Это утверждение можно пояснить другим способом. Если всю систему координат вращать с угловой скоростью  против часовой стрелки, то радиус-векторы в такой вращающейся системе координат будут неподвижны вместе со своими начальными фазами.

При построении векторных диаграмм величина радиус-вектора выражается не в амплитудном, а в эффективном (или действующем) значении тока или напряжения, которое непосредственно измеряется стрелочными электроизмерительными приборами.

Метод векторных диаграмм основан на том, что проекция геометрической суммы векторов на любую ось равна алгебраической сумме их проекций на ту же ось. Поэтому задача сложения выражений типа y = A·sin(ωt + φ) сводится к графической задаче сложения векторов. Этот метод особенно полезен при численных расчетах, так как все вычисления заменяются построением и измерением углов и отрезков. Он позволяет наглядно изобразить результаты измерений и расчетов и выявить важные закономерности (например, ответить на вопрос: принципиально можно или нельзя сбалансировать мост на переменном токе при том или ином расположении активных и реактивных сопротивлений в его плечах, не прибегая ни к каким расчетам).

Рассмотрим основные приемы построения векторных диаграмм, а в некоторых случаях, пользуясь векторными диаграммами, как наглядным пособием, дадим аналитический вывод для ряда важных величин.

Последовательная цепь

Поскольку по всем элементам цепи (рис. 28) протекает один и тот же ток, то построение начинают с вектора тока I.

Рис. 28.

Начало отсчета и направление вектора тока I выбирается произвольно.

Сопоставим начало отсчета вектора тока I с точкой «а» на рис. 28. (Здесь и далее везде под величиной тока I подразумевается его эффективное значение).

Если величина тока известна (измерена), то эту величину в виде вектора откладывают в подходящем масштабе в выбранном направлении (рис. 29).

Рис. 29.

Начало отсчета 0 совмещено с точкой «а» схемы, изображенной на рис. 28.

Если же величина тока не известна, а рассчитывается из известной величины, например, из общего напряжения, то току сначала приписывается произвольное (удобное) значение.

Далее поступают чисто формально. Обходя цепь (рис. 28) от точки «а» до точки «b», строят последовательно друг за другом векторы падения напряжений с учетом их начальных фаз (рис. 29). Напряжения на индуктивности, опережают ток на /2, поэтому вектор U_L1 строят вертикально вверх из точки 0 (U_L1 = ·L₁·I). На активном сопротивлении падение напряжения U_R1 совпадает с направлением тока (U_R1 = R₁·I). Вектор U_R1 строится параллельно направлению тока от конца вектора U_L1. Напряжение на емкости С₁ отстает по фазе от тока на /2. Вектор U_C1 = I/C₁ строится вниз от конца вектора U_R1. Вектор напряжения U_L2 = ·L₂·I строится вверх по той же линии, по которой был построен вектор U_C1, от его конца. На рис. 29 оба указанных вектора для наглядности построены параллельно друг другу.

К концу вектора U_L2 пристраивается вектор U_R2 и т.д. Конец вектора U_R3 = R₃·I будет соответствовать точке «b» (см. рис. 28). Таким образом, геометрическая сумма векторов изобразится вектором U, т.е. общим напряжением, приложенным к цепочке в точках «a» и «b».

Из векторной диаграммы видно, что общее напряжение U отстает от тока I на некоторый угол . Это означает, что вся цепочка носит емкостный характер.

Если ток с самого начала был известен, то из векторной диаграммы можно сразу найти величину напряжения U и сдвиг фазы .

Если величина тока заранее не была известна, и току произвольно приписывалась определенная величина, то после построения векторной диаграммы величина результирующего вектора напряжения должна быть равной напряжению приложенному ко всей цепочке. Сопоставляя эти два напряжения по их величине, находят коэффициент пересчета, с помощью которого находится истинное значение тока (и, разумеется, всех падений напряжений на элементах цепочки) и определяется (измеряют) угол .

Полное сопротивление (импеданс) цепи Z подсчитывается через активные и реактивные сопротивления элементов цепи по теореме Пифагора.

Элементы цепи могут располагаться в любом порядке. Можно сосредоточить все индуктивные сопротивления в одном месте цепочки, емкостные – в другом, активные – в третьем. От этого общий результат не изменится. На рис. 30 представлена схема, эквивалентная ранее рассмотренной на рис. 28.

Рис. 30.

Векторная диаграмма для рис. 30 строится точно так же, как было показано на рис. 29. Обе диаграммы называются векторной диаграммой напряжений.

Параллельная цепь

Изобразим те же элементы схемы на рис. 31.

U

(

a

)

L

2

R

1

C

1

R

2

C

2

R

3

L

1

(

b

)

Рис. 31.

Как видно из рисунка, ко всем нагрузкам (т.е. элементам схемы) приложено одно и тоже напряжение, однако токи, прошедшие через них, будут различны.

Построение векторной диаграммы в этом случае надо начинать с вектора напряжения (рис. 32).

Рис. 32.

Затем строят векторы силы токов поочередно для каждой нагрузки с учетом их фазовых углов аналогично предыдущему построению. Только теперь ток на индуктивном сопротивлении будет отставать, а на емкостном – опережать напряжение на угол /2. Во всем остальном (вместе с замечаниями) построение векторной диаграммы ничем не отличается от разобранного в предыдущем параграфе. Геометрическая сумма векторов определит величину и фазу искомого тока I .

Из рис. 32 видно, что вся нагрузка носит емкостный характер, так как ток опережает напряжение на угол .

Такая диаграмма называется диаграммой токов.

При сложении гармонических колебаний одинаковой частоты, описывающих ток или напряжение в сложных электрических цепях, совсем не обязательно представлять суммарные колебания в тригонометрическом виде. Для таких цепей важны окончательные значения величин токов и напряжений и углов сдвига между ними.

Разветвленная цепь

Построение векторной диаграммы для цепи, изображенной на рис. 28 начинают с контура (рис. 33). Ко всем элементам контура приложено одно и тоже напряжение U_bc.

Обозначим токи, текущие по ветвям контура, через I₁, I₂, I₃. Тогда общий ток, протекающий через весь контур, будет: I = I₁ + I₂ + I₃ (разумеется, этот же ток I будет протекать и через конденсатор С₂).

Рис. 33.

Прежде чем строить диаграмму токов для контура, необходимо построить диаграмму напряжений для тех его ветвей, где элементы цепи соединены последовательно¹ (рис. 34 – для левой ветви контура, рис. 35 – для правой ветви контура).

Рис. 34.

Рис. 35.

Теперь строят диаграмму токов для всего контура.

Выбирают направление вектора напряжения U (рис. 36) и вдоль него откладывают вектор напряжения U_bc.

Рис. 36.

Длина вектора U_bc соответствует величине приложенного к контуру напряжения. К вектору напряжения U_bc пристраивают ранее полученные треугольники напряжений (рис. 34 и рис. 35), изменив величину их сторон так, чтобы гипотенузы треугольников соответствовали длине вектора на диаграмме токов, сохранив при этом углы ₁ и ₂. Величины токов I₁ и I₂ также должны быть пересчитаны:

,
.

Затем векторно складывают токи I₁ и I₂.

Для этого к концу вектора I₂ (точка L) пристраивают вектор тока I₁ (изображен отрезком OК) в своем первоначальном направлении (LM = OK). Величина суммарного тока I′ изобразится отрезком OМ (на рисунке он не обозначен, чтобы не перегружать диаграмму лишними линиями).

Далее из точки O вверх по оси ординат строят вектор тока I₃ на емкости С₁.

Его величина равна I₃ = ·C₁·U_bc. Он изображен отрезком ON. Перенеся этот отрезок из точки O в точку М параллельно самому себе (МР = ON), закончим построение общего тока I, протекающего через весь контур. Величина тока I изображена отрезком OР. Углом  обозначен угол сдвига между построенным током и напряжением U_bc, поданным на контур.

Но тот же ток I протекает и через емкость С₂ (последовательное соединение). Поэтому для емкости С₂ и контура строят диаграмму напряжений.

Построение начинают с точки С. Из нее на направление вектора тока I опускают перпендикуляр. Вдоль его направления от точки С строят вниз вектор напряжения U_ab, так как напряжение на емкости отстает от тока на . Величина вектора напряжения равна: U_ab = и изображена на рис. 36 отрезком СR.

Вектор, соединяющий точки O и R, будет соответствовать вектору напряжения U, приложенному ко всей цепочке (рис. 28), а его длина – величине напряжения U. Найденный угол (обозначим его ) между током I и напряжением U дает величину искомого сдвига фаз.

На этом построение векторной диаграммы для всей цепи закончено, получены величина тока I и угол сдвига . Отметим, что вся цепочка носит индуктивный характер, так как напряжение U опережает ток I на угол .

ЛИТЕРАТУРА

• Благовещенский В.В., Зароченцева Е.П., Холмогоров В.Е., Шишкин Ю.Г. Электричество (Переменный ток). Описание лабораторных работ. Часть V. Работы № 42-51. Л., 1990.

• Детлаф А.А., Яворский Б.М. Курс физики. М., 1989.

• Зисман Г.А., Тодес О.М. Курс общей физики. М., 1972.

• Калашников С.Г. Электричество. М., 1977.

• Касаткин А.С., Немцов М.В. Электротехника. 4-е изд. М., 1983.

• Поливанов К.М. Линейные электрические цепи с сосредоточенными постоянными. М., 1972.

• Савельев И.В. Курс общей физики: Учеб. пособие. В 3-х т. 3-е изд., испр. М., 1987.

• Сивухин Д.В. Общий курс физики. М., 1990.

• Соловьев В.А., Яхонтова В.Е. Основы измерительной техники. Руководство к лабораторным работам по физике. Учеб. пособие. Л., 1980.

• Физическая энциклопедия / Гл. ред. А.М. Прохоров. Ред. Кол. Д.М. Алексеев, А.М. Балдин, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др. М., 1988-98.

ОПИСАНИЯ ЛАБОРАТОРНЫХ РАБОТ

УЧЕБНОЙ ЛАБОРАТОРИИ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА

ФИЗИЧЕСКОГО ФАКУЛЬТЕТА СПбГУ.