
топология / Прасолов В. В., Элементы комбинаторной и дифференциальной топологии
.pdf§ 4. Топология подмножеств евклидова пространства |
71 |
наименьшее целое число m, для которого по крайней мере одна точка x X принадлежит m элементам покрытия U и никакая точка x X не принадлежит более чем m элементам покрытия U. Будем говорить, что топологическая размерность компактного подмножества X Rn равна k, если k – наименьшее неотрицательное целое число, обладающее следующим свойством: для любого ε > 0 существует конечное покрытие множества X замкнутыми множествами диаметра меньше ε, имеющее порядок k + 1.
|
Т е о р е м а 4.7 |
(Лебег). Топологическая размерность n-мерного |
||||||||||||
симплекса |
n равна n. |
|
|
|
|
|
|
|
|
|
||||
|
Д о к а з а т е л ь с т в о |
(Шпернер |
[122]). |
Сначала |
докажем, что |
|||||||||
если U – конечное покрытие симплекса |
n замкнутыми множествами |
|||||||||||||
достаточно малого |
диаметра, то |
порядок |
U |
не меньше |
n + 1. Пусть |
|||||||||
n−1 |
, . . . , |
n−1 |
– |
(n − 1)-мерные грани |
|
|
n |
, ai – верши- |
||||||
0 |
|
n |
симплекса |
|
|
|||||||||
на |
симплекса |
n, |
противолежащая |
грани |
n−1. В топологическом |
|||||||||
|
|
|
|
|
|
|
|
|
n−1 |
|
i |
|
|
|
пространстве |
n |
подмножества |
n |
\ |
являются открытыми. Ясно |
|||||||||
|
|
|
|
|
|
|
|
i |
|
|
n |
. Пусть ε > 0 – |
||
также, что эти множества полностью покрывают |
|
|||||||||||||
число Лебега этого nоткрытого покрытия. Покажем, что |
если U – ко- |
|||||||||||||
нечное покрытие |
|
замкнутыми множествами диаметра меньше ε, |
||||||||||||
то |
порядок |
покрытия U |
не меньше |
n + 1. |
Пусть |
U = {U0, . . . , Um}. |
||||||||
Из того, что диаметр множества Uj меньше ε, следует, что Uj целиком лежит в некотором множестве n \ , т. е. Uj не пересекает грань
. Каждая вершина ai принадлежит некоторому множеству Uj. При этом множество Uj уже не может содержать других вершин симплекса n.
Каждому множеству Ui сопоставим грань |
n−1 |
– одну из тех граней, |
ϕ(i) |
которую Ui не пересекает. Получим соответствие ϕ : {0, . . ., m}→{0, . . . , n}. Для k = 0, . . . , n рассмотрим Ak – объединение тех множеств Ui, для ко-
|
n |
m |
n, ak Ak и Ak ∩ |
kn−1 = . |
|
торых ϕ(i) = k. Ясно, что k=0 Ak = i=0 Ui = |
|||||
|
замкнутости множеств A ) с помощью леммы Шпер |
|
|||
Из этих условий (и |
S |
S |
k |
|
- |
нера (см. с. 92) можно вывести, что множества Ak имеют общую точку x. В самом деле, пометим все точки симплекса n по следующему правилу: каждой точке сопоставим наименьший номер k множества Ak, которому она принадлежит. Согласно лемме Шпернера среди симплексов p-го барицентрического подразделения симплекса n есть симплекс с полным набором пометок. Выберем в нём произвольную точку xp. Из последовательности {xp} выберем сходящуюся подпоследовательность {xpq }. Точка
x = lim xpq принадлежит всем множествам Ak. В самом деле, каждому
q→∞
множеству Ak принадлежит одна из вершин симплекса, в котором мы

72 Глава II. Топология в евклидовом пространстве
выбирали точку xpq , а длина ребра такого симплекса стремится к нулю
при q → ∞. |
n |
замкнутыми |
Остаётся построить пример покрытия симплекса |
|
множествами сколь угодно малого диаметра, имеющего порядок n + 1. Рассмотрим (m + 1)-е барицентрическое подразделение симплекса n. Для каждой вершины m-го барицентрического подразделения рассмотрим множество, состоящее из содержащих ее замкнутых n-мерных симплексов (m + 1)-го барицентрического подразделения. Эти множества образуют требуемое покрытие. Чтобы убедиться в этом, достаточно рассмотреть первое барицентрическое подразделение. Барицентр принадлежит n + 1 множествам, а все остальные точки принадлежат меньшему
числу множеств. |
2 |
В определении топологической размерности участвует метрическая величина – диаметр множеств покрытия. Тем не менее, топологическая размерность действительно является топологическим инвариантом, т. е. сохраняется при гомеоморфизмах.
Т е о р е м а 4.8. Пусть X и Y – гомеоморфные компактные подмножества евклидова пространства. Тогда их топологические размерности равны.
Д о к а з а т е л ь с т в о. Пусть топологические размерности X и Y равны kX и kY . По условию существует гомеоморфизм h: X → Y . Для данного ε > 0 рассмотрим покрытие пространства Y открытыми шарами диаметра ε и рассмотрим также покрытие пространства X прообразами этих шаров при отображении h. Пусть δ – число Лебега этого открытого покрытия компактного пространства X. Согласно определению топологической размерности существует покрытие пространства X замкнутыми множествами U1, . . . , Um диаметра меньше δ, име-
ющее |
порядок kX + 1. Тогда {h(U1), . . . , h(Um)} – покрытие простран- |
|
ства |
Y замкнутыми |
множествами диаметра меньше ε, имеющее по- |
рядок kX + 1. Таким |
образом, kY 6 kX . Аналогично доказывается, что |
|
kX 6 kY . |
2 |
|
Теперь мы можем доказать знаменитую теорему Брауэра об инва-
риантности размерности [43]. |
|||
м а 4.9 |
(Брауэр). Если m = n, то открытое подмноже- |
||
Т е о р е m |
|
6 |
|
ство U Rn |
. |
не может быть гомеоморфно открытому подмноже- |
|
ству V R |
|
|
|
Д о к а з а т е л ь с т в о. Пусть h: U m→ V – гомеоморфизм. Множе- |
|||||||||
ство U содержит m-мерный симплекс |
. Топологическая размерность |
||||||||
m |
) R |
n |
равна m.n |
|
|
h( |
m) содер |
|
|
множества h( |
|
Компактное множество |
n |
|
|
- |
|||
жится в некотором симплексе |
. Покрытие симплекса |
|
замкнутыми |
||||||
множествами малого диаметра, имеющее порядок n, индуцирует покрытие
§ 4. Топология подмножеств евклидова пространства |
73 |
симплекса h( m) замкнутыми множествами малого диаметра, имеющее
порядок n. Поэтому m 6 n. Аналогично m > n. |
2 |
4.4.Канторово множество
Каждое число x [0, 1] можно записать в виде x = a13−1 + a23−2 +
+ . . . , где ai = 0, 1 или 2 (троичная |
запись |
числа x). Канторовым |
|||||
множеством называют множество C |
|
[0, 1], состоящее из тех чисел, |
|||||
|
|
|
|
3 |
−1 |
= |
|
у которых есть троичная запись без цифр 1. Например, число 1 |
· |
|
|||||
= 2 · 3−2 + 2 · 3−3 + 2 · 3−4 + . . . входит в C. |
|
|
|
|
|||
Пусть Ck – множество чисел x [0, 1], у которых есть троичная за-
пись с цифрой 0 или 2 на k-м месте.∞Например, C1 = h0, |
1 |
i h |
2 |
, 1i. |
|
3 |
3 |
||||
Каждое множество Ck замкнуто и C = |
Ck, поэтому множество C тоже |
||||
замкнуто. |
= |
|
|
|
|
kT1 |
|
|
|||
Т е о р е м а 4.10. Любое замкнутое подмножество A C является ретрактом пространства C, т. е. существует непрерывное отображение r : C → A, ограничение которого на A тождественно.
Д о к а з а т е л ь с т в о. Замкнутое множество A [0, 1] компактно, поэтому для любой точки c C существует точка a A, для которой d(c, A) = d(c, a). Таких точек a не может быть больше двух. Рассмотрим сначала случай, когда для точки c C существуют две такие точки a1 и a2, причем a1 < a2. В таком случае a1 < c < a2. Дополнение множества C всюду плотно, поэтому можно выбрать y 6C так, что a1 < y < c < a2. Для каждой точки x C ∩ [a1, y) положим r(x) = a1, а для каждой точки x C ∩ (y, a2] положим r(x) = a2. Построим таким образом отображе-
ние r для всех точек c C, для которых d(c, A) = d(c, a1) = d(c, a2). Построенное отображение определено корректно, потому что интервал
(a1, a2) не содержит точек множества A, а значит, отрезок [a1, a2] для точки c и отрезок [a01, a02] для точки c0 6= c не могут пересекаться.
Предположим, что c C – точка, для которой отображение r пока ещё не построено. Тогда существует ровно одна точка a A, для которой d(c, A) = d(c, a). Положим r(c) = a.
Для точки a A отображение r может определяться либо первым
способом, либо вторым, но в обоих случаях r(a) = a. |
2 |
С помощью теоремы 4.10 можно доказать следующее весьма неожиданное утверждение.
Т е о р е м а 4.11 (Александров [1]). Любое непустое компактное множество X Rn является образом канторова множества C при некотором непрерывном отображении.

74 |
Глава II. Топология в евклидовом пространстве |
Д о к а з а т е л ь с т в о. Пусть U1, U2, . . . – счётная база открытых множеств топологического пространства X. Для c C рассмотрим тро-
ичное разложение 0, c1c2c3 . . . , не содержащее цифр 1 (оно единственно).
|
|
|
|
∞ |
Точке c сопоставим множество P(c) = |
ϕi (c), где |
|||
|
|
|
|
iT1 |
|
(X Ui, |
= |
||
ϕi (c) = |
если ci = 2. |
|||
|
|
|
|
если ci = 0; |
|
Ui, |
|||
\
Легко проверить, что множество P(cx) состоит не более чем из одной точки. В самом деле, пусть a, b X и a 6= b. Тогда существует такое i,
что a Ui и b 6 Ui . Если ϕi (c) = Ui, то b 6 ϕi (c), а если ϕi (c) = X \ Ui, то a 6 ϕi (c). Поэтому множество P(c) не может одновременно содержать
обе точки a и b.
Если P(c) состоит из одной точки, то положим g(c) = P(c). Отобра-
|
c C |
∞ |
ϕi (c) 6= . |
жение g определено на множестве A = |
|
||
i=1 |
|||
|
|
T |
|
|
|
|
|
Легко проверить, что отображение g : A → X сюръективно. В самом
деле, для точки x X положим |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
ci |
0, |
|
|
если x |
Ui , |
|
|
|
|
|
||
|
|
|
|
|
= (2, |
|
|
если x |
Ui . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
Тогда c = 0, c1c2 . . . C и g(c) = x. |
|
|
|
|
|
|
|
||||||||||
Проверим |
теперь, что |
отображение g непрерывно. Пусть заданы |
|||||||||||||||
c = 0, c1c2 . . . A |
(ci 6= 1) |
и ε > 0. Выберем |
множество Uk |
так, что |
|||||||||||||
g(c) |
|
U и диаметр множества |
U |
|
|
меньше ε. Возьмем произвольную точ |
|||||||||||
|
k |
. . . |
|
|
|
|
k |
|
c |
a |
−2k |
|
- |
||||
ку a = 0, a1a2 |
|
A (ai = 1), для которой |
< 3 |
. Из неравенства |
|||||||||||||
|
|
−2k |
|
|
6 |
|
|
|
|
|
| − |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|c − a| < 3 |
следует, что |
ck = ak. Поэтому |
g(a) ϕk (a) = ϕk (c) = Uk. |
||||||||||||||
Таким образом, kg(a) − g(c)k < ε, а значит, отображение g непрерывно в точке c.
Покажем, наконец, что множество A замкнуто в C, т. е. множество
C \A открыто в C. Пусть c C \A. Тогда |
∞ |
ϕi (c) = , т. е. |
∞ |
(X \ϕi (c)) = |
= |
= |
|||
|
iT1 |
iS1 |
||
= X. Множества X \ ϕi (c) образуют открытое покрытие пространства X. Из этого покрытия можно выбрать конечное подпокрытие, поэтому
m |
(X \ ϕi (c)) = X для некоторого m > 1. В таком |
|
|
|
m |
||
i=1 |
случае ϕi (c) = . |
||||||
|
|
для которой |
c |
|
|
=1 |
|
S |
|
|
|
a <iT3−2m. Тогда |
|||
Пусть |
a C – произвольная точка, |
m |
| |
− |
|
| |
|
ai = ci |
для i = 1, . . . , m. Поэтому |
= ϕi (a) = , |
т. е. |
a C \ A. Это |
|||
|
|
|
iT1 |
|
|
|
|
означает, что множество C \ A открыто.

§ 5. Кривые на плоскости |
75 |
Мы построили непрерывное отображение g : A→X, где A C – замкнутое подмножество. Согласно теореме 4.10 существует непрерывная
r |
g |
ретракция r : C → A. Композиция отображений C −→ A −→ X является |
|
требуемым отображением. |
2 |
С л е д с т в и е (Пеано). Существует сюръективное отображение отрезка I на k-мерный куб Ik.
Д о к а з а т е л ь с т в о. Сначала построим непрерывное отображение f : C → Ik. Канторово множество C замкнуто, поэтому по теореме Титце отображение f можно продолжить до непрерывного отображения
F : I → Ik. |
2 |
§ 5. Кривые на плоскости
5.1.Теорема Жордана
Жордановой кривой называют образ C окружности S1 при непрерывном инъективном отображении f : S1 → R2. Инъективность означает, что f(x1) 6= f(x2) при x1 6= x2. В «Курсе анализа» [77] Жордан попытался доказать, что множество R2 \ C несвязно и состоит в точности из двух линейно связных компонент (теорема Жордана). Его доказательство было не вполне строгим. Первое полное доказательство теоремы Жордана предложил Веблен [134].
Мы уже доказывали теорему Жордана в том случае, когда кривая C представляет собой конечнозвенную ломаную (см. с. 19). Из кусочно-
линейной теоремы Жордана можно выве- |
|
|
|
|
сти общую теорему Жордана, аппроксими- |
|
|
|
|
|
|
|||
руя кривую C конечнозвенными ломаны- |
|
|
|
|
|
|
|
|
|
ми. Такое доказательство приведено в [129]. |
|
|
|
|
Мы, следуя [126], приведём доказательство |
|
|
|
|
|
|
|
||
теоремы Жордана, основанное на том, что |
|
|
|
|
|
|
|
|
|
граф K3,3 непланарен (теорема 1.3 на с. 21; |
|
|
|
|
напомним, что при доказательстве этой тео- |
|
|
|
|
|
|
|
|
|
ремы используется лишь кусочно-линейная |
Рис. 35. Жорданова кривая |
|||
теорема Жордана). Сначала мы докажем, |
и граф K3,3 |
|
|
|
что жорданова кривая разбивает плоскость. |
|
|
|
|
Т е о р е м а 5.1. Если C – жорданова кривая, то множество R2 \ C не является линейно связным.
Д о к а з а т е л ь с т в о. Проведём к кривой C опорные прямые и выберем на них точки A1 и A2, лежащие на кривой C. На двух дугах кривой C, заданных точками A1 и A2, можно выбрать точки B1 и B2 так,

76 Глава II. Топология в евклидовом пространстве
что отрезок B1B2 не будет пересекать кривую C (рис. 35); действительно, каждая из этих двух дуг является компактным множеством, поэтому пересечение дуги с любой прямой, параллельной опорным прямым, компактно. На отрезке B1B2 выберем точку A3. Если бы точки A3 и B3 можно было бы соединить путём, не пересекающим кривую C, то мы получили
бы вложение графа K3,3 в плоскость, чего не может быть. |
2 |
Докажем теперь следующее вспомогательное утверждение: незамкнутая дуга кривой не разбивает плоскость.
Т е о р е м а 5.2. Пусть A – простая дуга на плоскости, т. е. образ отрезка I при непрерывном отображении f : I → R2. Тогда мно-
жество R2 \ A связно.
Д о к а з а т е л ь с т в о. Пусть x, y R2 \ A. Множество A компактно, поэтому можно выбрать положительное число d так, что расстояния от x и y до A больше 3d. Отображение f равномерно непрерывно, поэтому A можно разбить на дуги A1, . . . , Ak (дуга Ai соединяет точки ai и ai+1) так, что расстояние от точки ai до любой точ-
ки дуги Ai |
не превосходит d (здесь i = 1, . . . , k). Пусть минимальное |
|
расстояние0 |
между0 |
точками дуг Ai и Aj, где 1 6 i 6 j − 2 6 k − 2, равно |
d . Ясно, что d 6 d. Каждую дугу Ai разобьём на дуги Ai1, . . . , Aiki (дуга Aij соединяет точки aij и ai,j+1) так, что расстояние от точки aij до любой точки дуги Aij меньше d0/4. Пусть Gi – граф, образованный сторонами квадрата с центрами в точках aij ; стороны всех этих квадратов параллельны двум фиксированным прямым и длины сторон квадратов равны d0/2. Графы Gi и Gj пересекаются тогда и только тогда, когда |i − j| 6 1.
Граф G = G1 . . . Gk разбивает плоскость на связные области, среди которых есть ровно одна неограниченная область F. Каждая точка дуги A принадлежит какой-то ограниченной области, поэтому A не пересекает F. Следовательно, достаточно доказать, что x, y F.
Предположим, что точка x принадлежит ограниченной области графа G. Граф G является 2-связным, поэтому в G найдётся цикл C, внутри которого лежит точка x. Выберем цикл C так, что он принадлежит графу Gi Gi+1 . . . Gj, причем разность j − i минимальна. Покажем, что в таком случае j − i 6 1. Предположим, что j − i > 2. Можно считать, что число рёбер цикла C, не принадлежащих Gj−1, минимально. Цикл C содержит по крайней мере по одному ребру из непересекающихся графов Gj−2 и Gj (имеются в виду ребра, не принадлежащие Gj−1). Кроме того, после выбрасывания всех рёбер графа Gj−1 нарушается связность цикла C. Это означает, что цикл C содержит по крайней мере два непересекающихся участка, проходящих по графу Gj−1. Эти два участка можно соединить путём γ, проходящим по рёбрам графа Gj−1. Путь γ разбивает
§ 5. Кривые на плоскости |
77 |
цикл C на два цикла. Точка x лежит внутри одного из этих циклов. Но у каждого из этих циклов число рёбер, не принадлежащих Gj−1, строго меньше, чем у цикла C. Получено противоречие.
Итак, точка x принадлежит внутренней области графа Gi Gi+1. Но этого не может быть, так как точка x лежит вне круга радиуса 3d с центром ai , а граф Gi Gj+1 лежит внутри этого круга. Полученное противоречие означает, что точка x принадлежит неограниченной области графа G. Точка y принадлежит той же самой области, поэтому x и y
можно соединить путём, лежащим в R2 \ A. |
2 |
Мы уже доказали, что жорданова кривая разбивает плоскость. Теперь можно доказать оставшуюся часть теоремы Жордана.
Т е о р е м а 5.3. Жорданова кривая C разбивает плоскость в точности на две линейно связные области, причем границей обеих этих областей служит кривая C.
Д о к а з а т е л ь с т в о. Пусть Ω – одна из линейно связных областей, на которые кривая C разбивает плоскость, c – произвольная точка кривой C. Если из кривой C выбросить сколь угодно малую дугу δ, содержащую точку c, то оставшаяся дуга A = C \ δ не разбивает плоскость. Поэтому точку x Ω можно соединить с точкой y, лежащей в другой компоненте связности, путём γ, не пересекающим A. Путь γ должен пересекать кривую C, поэтому он пересекает дугу δ. У пути γ есть участок, который соединяет точку x с точкой дуги δ и целиком принадлежит области Ω (за исключением точки дуги δ). Таким образом, граница области Ω содержит всюду плотное подмножество кривой C, а значит, она содержит и всю кривую C, поскольку граница – замкнутое множе-
ство. |
|
|
|
|
|
Остаётся |
доказать, что |
количество |
|
|
|
связных областей множества |
R2 \ C не мо- |
||||
|
|
||||
|
|
||||
жет быть больше 2. Предположим, что |
|
|
|||
точки x1, x2, x3 принадлежат трём раз- |
|
|
|||
личным областям Ω1, Ω2, Ω3 множества |
|
|
|||
R2 \ C. Пусть δ1, δ2, δ3 – попарно непере- |
|
|
|||
секающиеся |
дуги кривой C. В области |
|
|
||
|
|
||||
Ω1 точку x1 можно соединить путём γ1j с некоторой точкой дуги δj. При этом можно добиться, чтобы пути γ11, γ12 и γ13 пе-
ресекались только в точке x1. Для этого в окрестности точки пересечения эти пути нужно перестроить так, как показано на рис. 36.
Для точек x2 и x3 пути γ2i и γ3i определим аналогично. Добавив к путям γij, где i, j = 1, 2, 3, части дуг δi, получим вложение графа K3,3
в плоскость, чего не может быть. |
2 |
78 |
Глава II. Топология в евклидовом пространстве |
5.2.Теорема Уитни–Грауштейна
Пусть S1 = {e2πis |
т. е. γ (s) = (x(s), y(s)), dγ (s)
s R} и γ : S1 → R2 – гладкая замкнутая кривая, где x и y – непрерывно дифференцируемые функ-
ds
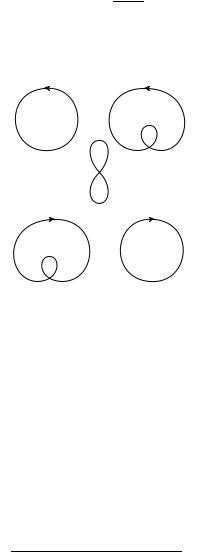
кривой γ число оборотов вектора v(s) при изменении s от 0 до 1. При этом каждый оборот против часовой стрелки считается со знаком плюс, а каждый оборот по часовой стрелке считается со знаком минус. Примеры
кривых малых степеней изображены на рис. 37. |
|
|
|
||||||||
|
|
|
|
|
|
|
Будем говорить, что гладкие замкну- |
||||
|
|
|
|
|
|
|
тые кривые γ0 и γ1 регулярно гомотоп- |
||||
|
|
|
|
|
|
|
ны, если существует семейство гладких |
||||
|
|
|
|
|
|
|
замкнутых кривых γt , гладко зависящее |
||||
= |
|
= |
|
|
от t [0, 1] |
(имеется в виду, что γt = γ0 |
|||||
|
|
|
|
|
|
|
при t = 0 и γt = γ1 |
при t = 1). Гладкая |
|||
|
|
|
|
|
зависимость от t означает, что отоб- |
||||||
|
|
|
|
|
|
|
ражение (s, t) 7→γt (s) является непре- |
||||
|
|
= |
|
|
|
|
рывно дифференцируемым отображени- |
||||
|
|
|
|
|
|
ем из [0, 1] × [0, 1] в R2. |
|
||||
|
|
|
|
|
|
|
Т е о р е м а |
5.4 |
(Уитни–Грауштейн |
||
|
|
|
|
|
|
|
[145]). Кривые γ0 и γ1 регулярно гомо- |
||||
|
|
|
|
|
|
|
топны тогда и только тогда, когда |
||||
= |
− |
= |
− |
|
их степени равны. |
|
|
||||
|
|
Д о к а з а т е л ь с т в о. |
Пусть кри- |
||||||||
Рис. 37. Примеры кривых ма- |
вые γ0 и |
γ1 |
регулярно |
гомотопны |
|||||||
лых степеней |
|
|
|
|
и Nt – степень гладкой кривой γt . Ясно, |
||||||
что Nt – целое число, причем Nt непрерывно зависит от t. Поэтому Nt – константа и N0 = N1.
Предположим теперь, что γ0 и γ1 – гладкие замкнутые кривые, степени которых равны N. С помощью регулярной гомотопии кривые γ0 и γ1 можно заменить на кривые длины 1, для которых γ0 (0) = γ1 (0) = (0, 0) и γ00 (0) = γ10 (0) = (1, 0). В таком случае можно считать, что s [0, 1] – натуральный параметр, т. е. kγ00 (s)k = kγ10 (s)k = 1 при всех s.
Запишем векторы скоростей кривых γ0 и γ1 в виде v0 (s) = e
и v1 (s) = eiϕ1 (s) , где ϕ0 (0) = ϕ1 (0) = 0 и ϕ0 (1) = ϕ1 (1) = 2πN. Положим ϕt (s) = (1 − t)ϕ0 (s) + tϕ1 (s) и рассмотрим кривую γht с вектором скорости
Z s
vt (s) = eiϕt (s) : γht (s) = eiϕt (τ) dτ . При t 6= 0, 1 кривая γht не обязательно
0
) Степень гладкой замкнутой кривой – это совсем не то же самое, что степень алгебраической кривой.

§ 5. Кривые на плоскости |
79 |
замкнутая, но с помощью этой кривой можно построить замкнутую кри-
|
t |
|
|
|
t |
− |
t |
s |
|
d− |
1 |
e |
|
d |
d |
|
. |
|
d |
|||
|
|
|
|
Z0 |
|
Z0 |
|
|
|
|||||||||||||
вую γ |
|
(s) |
= γh (s) |
|
sγh (1) = |
eiϕt (τ) dτ |
s |
|
iϕt (τ) |
|
τ |
|
Нужно лишь |
|||||||||
проверить, что кривая γt |
гладкая, т. е. |
|
γt (1) = |
|
γt (0) |
и |
|
γt (s) 6= 0. |
||||||||||||||
ds |
ds |
ds |
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ясно, что |
|
d |
γt (s) = eiϕt (s) − Z0 |
eiϕt (τ) dτ = vt (s) − γht (1). Равенство ско- |
||||||||||||||||||
|
ds |
|||||||||||||||||||||
ростей при s = 0 и при s = 1 следует из того, что vt (0) = vt (1), поскольку |
||||||||||||||||||||||
ϕt (0) = 0 |
и |
ϕt (1) = 2πN. Для |
доказательства |
того, |
что |
vt (s) 6= γht (1), |
||||||||||||||||
достаточно заметить, что kvt (s)k = 1, а kγht (1)k < 1, поскольку kγht (1)k =
= |
|
Z0 |
1 eiϕt (τ) dτ |
|
6 Z0 |
1 |
|
eiϕt (τ) |
|
dτ 6 1, причем eiϕt (τ) – не постоянная |
||||
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Наметим |
|
|
|
|
|
|
|
|
– |
|
- |
|
функция. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ещё один подход к доказательству теоремы Уитни |
|
Грау |
|
|||||||
штейна. После малого шевеления можно считать, что кривая имеет лишь конечное число точек самопересечения. Назовём простой петлёй часть ω кривой γ, обладающую следующими свойствами: 1) ω начинается и кончается в точке самопересечения кривой γ; 2) ω не имеет самопересечений (но она может пересекать другие части кривой γ). Легко доказать, что любая гладкая кривая с конечным (ненулевым) числом точек самопересечения имеет простую петлю. Далее, для простой петли ω кривой γ существует регулярная гомотопия, при которой изменяется только ω, причём после гомотопии мы получаем новую простую петлю ω0, которая не пересекает γ. В конце концов мы получим окружность с маленькими петельками – внешними и внутренними. Эти петельки можно менять местами, протаскивая одну петельку через другую. Кроме того, несложно построить регулярную гомотопию, которая уничтожает пару петелек, одна из которых внутренняя, а другая внешняя.
Т е о р е м а 5.5 (см. [137] и |
[73]). Степень гладкой замкнутой |
|||||
несамопересекающейся кривой γ равна ±1. |
|
|||||
Д о к а з а т е л ь с т в о |
(Хопф |
[73]). |
После |
регулярной гомотопии |
||
можно считать, что длина |
кривой γ равна 1 и |
отображение γ : S1 = |
||||
= {e2πis } → R2 таково, что |
|
dγ |
|
= 1 при |
всех |
s [0, 1]. Пусть T – |
|
|
|
|
|
|
|
ми 0 6 x 6 y 6 1. |
|
|
|
|
|
|
треугольник на плоскости с координатами x и y, заданный неравенстваРассмотрим отображение f : T → S1, заданное формулой
γ (y) − γ (x) ,
kγ (y) − γ (x)k
f(x, y) = γ0 (x),
−γ0 (0),
если 0 < y − x < 1;
если x = y;
если x = 0 и y = 1.

80 Глава II. Топология в евклидовом пространстве
(Отметим, что если x = y, то γ0 (x) = γ0(y), а если если x = 0 и y = 1,
то |
− |
γ0 |
(0) = |
− |
γ0 |
(1).) Для накрытия p : |
R |
1 |
→ |
S1 |
, заданного формулой |
||
|
|
2πis |
|
|
|
|
|
|
|||||
p(s) = e |
|
, существует поднятие отображения f, т. е. такое отображение |
|||||||||||
F : T → R1, что pF = f. При этом 2π deg γ = F(1, 1) − F(0, 0) = [F(1, 1) − − F(0, 1)] + [F(0, 1) − F(0, 0)].
Разность F(1, 1) − F(0, |
1) соответствует углу поворота вектора γ (1) − |
− γ (x) = γ (0) − γ (x) = v(x) |
при изменении x от 0 до 1 (верхняя сторона |
треугольника T). Если в качестве γ (0) выбрать точку касания кривой γ |
|
с какой-либо опорной прямой (рис. 38), то этот угол поворота будет равен |
|
|
|
|
±π (знак совпадает со знаком чис- |
|
|
|
|
ла deg γ). Разность F(0, 1) − F(0, 0) |
|
|
|
|
соответствует углу поворота векто- |
|
|
|
γ |
ра γ (y) − γ (0) = −v(y) при измене- |
|
|
|
|
нии y от 0 до 1. Этот угол поворота |
|
|
γ |
|
||
|
тоже равен ±π, причем знак снова |
|||
|
|
|
||
Рис. 38. |
|
совпадает со знаком deg γ, посколь- |
||
Выбор точки γ (0) |
ку векторы v и −v вращаются в од- |
|||
|
|
|
ном направлении. |
2 |
Пусть γ : S1 → R2 – гладкая замкнутая кривая с конечным числом точек самопересечения, причем все её точки самопересечения двукратные. Выберем на кривой γ точку x0, не являющуюся точкой самопересечения. Для точки самопересечения xi с номером i определим число Wi по следующему правилу. Будем идти из точки x0 вдоль кривой γ в направлении, согласованном с её ориентацией. Когда мы будем первый раз проходить через точку xi, нарисуем касательный вектор v1, соответствующий направлению движения; когда мы будем проходить через эту точку второй раз, нарисуем второй касательный вектор v2. Если репер (v1, v2) ориентирован отрицательно, то Wi = 1, а если этот репер ориентирован поло-
жительно, то Wi |
= −1. Числом Уитни называют число W(γ, x0) = Wi, |
|||
где суммирование ведётся по всем точкам самопересечения кривойP. |
||||
|
|
|
|
γ |
Т е о р е м а |
5.6 (Уитни |
[145]). Если |
deg γ – степень кривой γ, |
|
а W(γ, x0) – число Уитни, то deg γ = W(γ, x0) ± 1. |
|
|||
γ |
|
γ |
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
|
|
|
Рис. 39. Перестройка кривой γ
