
топология / Прасолов В. В., Элементы комбинаторной и дифференциальной топологии
.pdfПредисловие |
11 |
ни. С помощью взрезанного джойна доказывается, что некоторые n-мер- ные симплициальные комплексы нельзя вложить в R2n.
Вглаве IV обсуждаются весьма разнообразные темы – двумерные поверхности, накрытия, локальные гомеоморфизмы, графы на поверхностях (род графа, раскраски карт на графах), расслоения, гомотопические группы.
Вглаве V мы обращаемся к дифференциальной топологии. Здесь обсуждаются гладкие многообразия и приложения гладких отображений в топологии. Сначала вводится основная техника (гладкие разбиения единицы, теорема Сарда) и обсуждается важный для всей топологии пример – многообразия Грассмана. Затем обсуждаются понятия, связанные с касательным пространством: векторные поля и дифференциальные формы. После этого доказываются важные для работы с гладкими многообразиями теоремы о существовании вложений и погружений (в том числе и о вложениях некомпактных многообразий в качестве замкнутых подмножеств). Помимо этого доказывается, что замкнутое неориентируемое многообразие размерности n нельзя вложить в Rn+1 и выясняется, какие двумерные поверхности вкладываются в RP3. Далее вводится гомотопический инвариант – степень гладкого отображения. С помощью степени определяется индекс особой точки векторного поля. Доказывается теорема Пуанкаре–Хопфа о гомотопической классификации отображений Mn → Sn. Приводится конструкция Понтрягина, интерпретирующая
πn+k (Sn) как множество классов оснащённо кобордантных многообразий размерности k в Rn+k. Глава завершается теорией Морса, которая связывает топологическое строение многообразия с локальными свойствами особых точек невырожденной функции на данном многообразии. Приводятся явные примеры функций Морса на некоторых многообразиях, в том числе и на многообразиях Грассмана.
Глава VI посвящена явным вычислениям фундаментальной группы некоторых пространств и приложениям фундаментальной группы. Прежде всего доказывается теорема о задании фундаментальной группы CW -комплекса образующими и соотношениями и приводятся некоторые примеры применения этой теоремы. Иногда фундаментальную группу более удобно вычислять с помощью точной последовательности расслоения. Так обстоит дело, например, с фундаментальной группой SO(n). При вычислении фундаментальной группы нередко бывает полезна теорема ван Кампена о строении фундаментальной группы объединения двух открытых множеств. Её можно использовать, например, для вычисления фундаментальной группы дополнения узла. В конце главы приводится
другая теорема ван Кампена – о вычислении фундаментальной группы дополнения алгебраической кривой в CP2. Соответствующие вычисления
12 |
Предисловие |
для конкретных кривых довольно сложные; здесь есть много интересных результатов, но многое пока остаётся не до конца понятным.
Одна из главных целей книги состоит в том, чтобы продвинуться в изучении свойств топологических пространств (и особенно многообразий) столь далеко, сколь это возможно без привлечения сложной техники. Этим она отличается от большинства книг по топологии.
Книга рассчитана на читателей, знакомых с основными понятиями геометрии, линейной алгебры и анализа. В частности, предполагается некоторое знакомство с открытыми, замкнутыми и компактными множествами в евклидовом пространстве.
Для самостоятельного обдумывания в книге предлагаются три вида заданий. 1) Упражнения, которые не должны вызвать затруднений; их решения не приводятся. 2) Задачи, которые уже не столь просты, а потому в конце книги приведены их решения. 3) Задачи «со звёздочкой», каждая из которых составляет содержание отдельной научной статьи. В качестве задач эти утверждения сформулированы для того, чтобы не перегружать основной текст книги. Решения этих задач тоже приведены в конце книги. Задачи составлены по материалам семинаров по топологии для студентов I и II курса Независимого московского университета, которые автор вёл в 2002 г.
Во время работы над этой книгой я получал финансовую поддержку от Российского фонда фундаментальных исследований согласно проекту 01–01–00660.
Основные определения
Для начала нам потребуются лишь основные понятия топологии. Приведём их определения.
Топологическим пространством называют множество X, в котором выделена система подмножеств τ , обладающая следующими свойствами:
1)пустое множество и всё множество X принадлежат τ ;
2)пересечение конечного числа элементов τ принадлежит τ ;
3)объединение любого семейства элементов τ принадлежит τ . Множества, принадлежащие τ , называют открытыми. Окрестно-
стью точки x X называют любое открытое множество, содержащее x. Множества, дополнения которых открыты, называют замкнутыми.
Важнейшим примером топологического пространства служит евклидово пространство Rn. Открытыми множествами в Rn являются шары
Dan,ε = {x Rn | kx − ak < ε0 |
} и всевозможные их объединения. |
|
Семейство множеств τ |
τ называют базой топологии τ , если0 |
любой |
элемент системы τ является объединением элементов системы τ . |
|
|
У п р а ж н е н и е 1. Докажите, что семейство множеств τ 0 τ яв- |
||
ляется базой топологии τ тогда и только тогда, когда для любой точки x и для любой её окрестности U найдётся такое множество V τ 0, что x V U.
У п р а ж н е н и е 2. Докажите, что семейство множеств τ 0 является базой некоторой топологии тогда и только тогда, когда для любых двух множеств U, V τ 0 и для любой точки x U ∩ V найдется такое множество W τ 0, что x W U ∩ V .
Топологическое пространство X называют пространством со счётной базой, если у него есть база, состоящая из счётного семейства множеств.
Например, открытые шары Dan,ε, где число ε и все координаты точки a рациональны, образуют счётную базу пространства Rn.
Если X – топологическое пространство, то на любом его подмножестве Y можно ввести индуцированную топологию, считая открытыми множествами пересечения Y с открытыми подмножествами X. Это позволяет снабдить сферу Sn = {x Rn+1 | kxk = 1} структурой топологического пространства.
Отображение одного топологического пространства в другое называют непрерывным, если прообраз любого открытого множества от-

14 Основные определения
крыт. Эквивалентное условие: прообраз любого замкнутого множества замкнут.
При доказательстве того, что отображение f непрерывно, часто бывает удобно пользоваться следующим критерием непрерывности: отображение f : X → Y непрерывно тогда и только тогда, когда для любой точки x X и для любой окрестности U точки f(x) существует окрестность V(x) точки x, образ которой целиком лежит в U. Действительно, если выполняется второе условие, то множество f−1 (U), где U – открытое множество, можно представить в виде
f−1 (U) = |
V(x), поэтому оно открыто. В другую сторону утвержде- |
||||||||||
x fS1 |
(U) |
|
−1 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
ние очевидно: в качестве V(x) можно взять f |
|
(U). |
|
|
|
n |
|
m непре |
|
||
У п р а ж н е н и е 3. Докажите, что |
отображение f : |
R |
→ R |
- |
|||||||
|
|
|
n |
|
|
|
|||||
рывно тогда и только тогда, тогда для любого x R |
|
и для любого ε > 0 |
|||||||||
существует такое δ > 0, что если kx − ak < δ, то kf(x) − f(a)k < ε.
Втопологии довольно часто используется следующее утверждение
осклейке непрерывных отображений.
Т е о р е м а 0.1. Пусть X = X1 . . . Xn, причём множества X1,
. . . , Xn замкнуты. Рассмотрим отображение f : X → Y и его ограничения fi = f|Xi . Отображение f непрерывно тогда и только тогда, когда непрерывны все отображения fi .
Д о к а з а т е л ь с т в о. Ясно, что если отображение f непрерывно, то все отображения fi тоже непрерывны. Предположим, что все отоб-
ражения f |
|
непрерывны и C |
Y – произвольное замкнутое множество. |
|||||||||||||||
|
i |
|
|
|
−1 |
(C)0 |
|
−1 |
(C) ∩ Xi |
замкнуто0 в Xi , т. е. существует |
||||||||
Тогда множество Ci = fi |
= f |
|
||||||||||||||||
замкнутое0 |
в X множество Ci |
, для которого Ci = Ci ∩ Xi . Оба множества |
||||||||||||||||
Ci и Xi замкнуты в X, поэтому множество Ci тоже замкнуто в X. Следо- |
||||||||||||||||||
вательно, множество f−1 (C) = C1 . . . Cn замкнуто в X. |
2 |
|||||||||||||||||
Отображение f : X |
→ |
Y называют гомеоморфизмом, если оно вза |
- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|||
имно однозначно и оба отображения f и f |
|
|
непрерывны. Топологические |
|||||||||||||||
пространства X и Y называют в таком случае гомеоморфными. |
|
|
||||||||||||||||
У п р а ж н е н и е 4. |
Докажите, что пространства Rn и Sn \ {x0} го- |
|||||||||||||||||
меоморфны. |
|
Докажите, что Sn+m−1 |
|
Sn−1 |
|
|
|
Sm−1. (Предпо |
|
|||||||||
З а д а ч а 0.1. |
|
≈ R |
n |
× |
- |
|||||||||||||
лагается, что сфера |
S |
n−1 |
|
|
|
|
|
\n+m−1 |
|
|
|
|||||||
|
|
расположена в S |
|
стандартно.) |
|
|
||||||||||||
Топологическое пространство X называют дискретным, если любое его подмножество открыто (эквивалентное определение: любое его подмножество замкнуто). Топологию дискретного топологического пространства называют дискретной. Если X – дискретное топологическое пространство, а Y – произвольное топологическое пространство, то любое отображение f : X → Y непрерывно.
Основные определения |
15 |
Топологическое пространство X называют связным, если оно не содержит собственных подмножеств, которые одновременно открыты и замкнуты. Иными словами, если множество A X одновременно открыто
изамкнуто, то либо A = , либо A = X.
Уп р а ж н е н и е 5. Докажите, что пространство Rn связно.
Уп р а ж н е н и е 6. Докажите, что если X – связное топологическое пространство, а Y – дискретное топологическое пространство, то любое непрерывное отображение f : X → Y постоянно, т. е. f(X) состоит из одной точки.
Множество X называют метрическим пространством, если для любых двух точек x, y X определено число d(x, y) > 0, причем выполняются следующие свойства:
1)d(x, y) = d(y, x);
2)d(x, y) + d(y, z) > d(x, z) (неравенство треугольника);
3)d(x, y) = 0 тогда и только тогда, когда x = y.
Число d(x, y) называют расстоянием между точками x и y.
Для любого метрического пространства X открытые шары Dan,ε = = {x X | d(x, a) < ε} образуют базу некоторой топологии. Эту топологию называют топологией, индуцированной метрикой d. Если X – топологическое пространство, топология которого индуцируется некоторой метрикой, то в таком случае X называют метризуемым топологическим пространством.
Топологическое пространство называют компактным, если из любого его покрытия открытыми множествами можно выбрать конечное подпокрытие.
Уп р а ж н е н и е 7. Докажите, что сфера Sn компактна, а пространство Rn некомпактно.
Уп р а ж н е н и е 8. Докажите, что непрерывный образ компактного пространства компактен.
З а д а ч а 0.2. Пусть K – компактное метрическое пространство с метрикой ρ. Предположим, что f : K → K – непрерывное отображение, для которого ρ f(x), f(y) < ρ(x, y) для любых x, y K, x 6= y. Докажите, что отображение f имеет неподвижную точку.
На прямом произведении X × Y топологических пространств X и Y
можно задать топологию прямого произведения. Для этого нужно считать открытыми множествами в X × Y прямые произведения открытых множеств в X и Y , а также всевозможные их объединения.
Топология прямого произведения возникает из естественного требования непрерывности проекций pX (x, y) = x и pY (x, y) = y. В самом деле, чтобы эти отображения были непрерывны, множества U × Y и X × V , где U X и V Y – открытые множества, должны быть открытыми. Ми-
16 |
Основные определения |
|
|
|
|
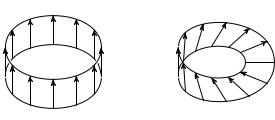
Рис. 1. Цилиндр и лист Мёбиуса
нимальная топология на множестве X × Y , включающая все указанные множества, совпадает с топологией прямого произведения.
Отметим, что прямым произведением S1 × I, где I – отрезок [0, 1], является цилиндр (рис. 1 (а)), а не лист Мёбиуса (рис. 1 (б)). Дело в том, что хотя и для листа Мёбиуса можно указать естественную проекцию на S1, но естественную проекцию на I для него указать не удаётся.
Для любого подмножества Y топологического пространства X можно определить факторпространство X/Y , отождествив все точки множества Y друг с другом. При этом точками пространства X/Y служат все точки множества X \ Y и одна точка Y . Множество в X/Y является открытым тогда и только тогда, когда его прообраз при естественной проекции p : X → X/Y открыт.
Факторпространство можно определить также и в том случае, когда на множестве X задано отношение эквивалентности . А именно, точками факторпространства X/ служат классы эквивалентности; множество в X/ открыто тогда и только тогда, когда его прообраз при естественной проекции p : X → X/ открыт. (Если x1 x2 тогда и только тогда, когда x1, x2 Y X, то мы получаем предыдущую конструкцию.)
Глава I
Графы
В этой главе теория графов обсуждается существенно более подробно, чем это обычно делается в курсах топологии. При этом § 1 и 3 относятся собственно к теории графов и в дальнейшем не используются. Поэтому читатель, у которого нет интереса к теории графов, может их пропустить.
§ 1. Топологические и геометрические свойства графов
Возьмём в пространстве R3 несколько точек A1, . . . , An и соединим некоторые из них попарно непересекающимися кривыми. Полученное множество с индуцированной из R3 топологией называют графом, или 1-мерным комплексом. Точки A1, . . . , An называют при этом вершинами, или 0-мерными клетками, а соединяющие их кривые называют рёбрами, или 1-мерными клетками. Количество рёбер, выходящих из вершины графа, называют степенью вершины. В том случае, когда из любой вершины графа можно пройти по его рёбрам в любую другую вершину, граф называют связным.
Граф может иметь петли (рёбра, начало и конец которых совпадают) и двойные рёбра (несовпадающие рёбра, имеющие одну и ту же пару вершин).
Последовательность попарно различных вершин v1, . . . , vn, соединённых рёбрами v1v2, v2v3, . . . , vnv1, называют циклом.
1.1.Планарные графы
Граф G называют планарным, если его можно расположить на плоскости так, чтобы его рёбра попарно не пересекались. При этом, вообще говоря, рёбра могут быть произвольными кривыми линиями, но легко убедиться, что рёбра можно считать конечнозвенными ломаными. Более того, Вагнер [135] и Фари [55] независимо доказали следующее утверждение.
18 |
Глава I. Графы |
Т е о р е м а 1.1. |
Любой планарный граф можно так вложить |
вплоскость, что все его рёбра будут прямолинейными отрезками.
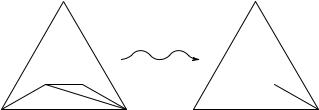
До к а з а т е л ь с т в о. Требуемое утверждение достаточно доказать для максимальных планарных графов. (Планарный граф называют максимальным, если после добавления любого дополнительного ребра он перестает быть планарным.) Ясно, что у максимального планарного графа все грани (области, на которые он разбивает плоскость) содержат ровно
по три ребра. Пусть G – максимальный планарный граф, содержащий v > 4 вершин (при v < 4 утверждение очевидно). Выберем в графе G произвольную вершину V1, отличную от вершин криволинейного треугольника, ограничивающего граф G. Пусть G1 – граф, который получается из графа G после выбрасывания вершины V1 и выходящих из неё рёбер. В графе G1 все грани, кроме грани F1, которой принадлежала выброшенная вершина V1, являются треугольными. Грань F1 ограничена циклом C1. Среди вершин цикла C1 выберем вершину V2, отличную от вершин треугольника, ограничивающего граф G, и рассмотрим граф G2, который получается из графа G1 после выбрасывания вершины V2 и выходящих из нее рёбер. В графе G2 грань F2, которой принадлежала вершина V2, не обязательно ограничена циклом (соответствующий пример приведён на рис. 2).
Чтобы грань F2 была ограничена некоторым циклом C2, вершину V2 нужно выбрать специальным образом. А именно, пусть цикл C1 содержит вершину V степени 2 (имеется в виду степень вершины в графе G1), причём V отлична от вершин ограничивающего граф G треугольника. Тогда в качестве V2 мы выбираем именно эту вершину V . Концы рёбер, выходящих из вершины V , соединены ребром, поэтому после выбрасывания вершины V мы получим цикл C2. Если же цикл C1 не содержит вершин степени 2, то в качестве V2 можно выбрать произвольную вершину.
Продолжая аналогичные операции, получим последовательность графов G, G1, G2, . . . , Gv−3, где Gv−3 – граф, состоящий из трёх вершин, попарно соединённых рёбрами; при этом граница каждой грани Fi – цикл.
Рис. 2. Граница грани – не цикл
§ 1. Топологические и геометрические свойства графов |
19 |
Рис. 3. Область видимости для |
Рис. 4. Область видимости для |
невыпуклого четырёхугольника |
одной из новых граней |
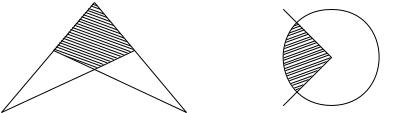
Построим теперь последовательно требуемое вложение графа G, начиная с графа Gv−3. В качестве вложения графа Gv−3 возьмём произвольный треугольник. В качестве вершины Vv−3 возьмём произвольную точку внутри этого треугольника. Точку Vv−3 нужно соединить с двумя или тремя вершинами треугольника. После этого треугольник разобьется либо на 3 треугольные области, либо на треугольную и невыпуклую четырёхугольную. Если вершину Vv−4 нужно поместить в треугольную область, то это делается произвольным образом. Если же вершину Vv−4 нужно поместить в невыпуклую четырёхугольную область, то поместим её в область, заштрихованную на рис. 3. Это – область, из которой видны все вершины цикла. В дальнейшем, исходя из области видимости, мы на каждом шаге снова будем получать некоторую область видимости – непустое открытое множество (рис. 4). Вершину Vi−1 нужно каждый раз помещать в область
видимости. |
2 |
Для доказательства непланарности графов обычно используется простейший вариант теоремы Жордана – для конечнозвенных ломаных.
Т е о р е м а 1.2 (кусочно-линейная теорема Жордана). Пусть C – замкнутая несамопересекающаяся конечнозвенная ломаная на плоскости R2. Тогда R2 \ C состоит ровно из двух связных областей, причём границей каждой из них служит C.
Д о к а з а т е л ь с т в о. Выберем некоторый фиксированный круг D, пересекающий ломаную C по отрезку. Из каждой точки множества R2 \ C можно сколь угодно близко подойти к ломаной C, не пересекая ее. Затем, идя вдоль ломаной C, можно войти в круг D. Ломаная C делит круг D на две части, поэтому количество областей не больше двух.
Остаётся доказать, что множество R2 \ C несвязно. Пусть x R2 \ C
иl – произвольный луч с началом x. Пересечение луча l с ломаной C состоит их нескольких точек и отрезков. Каждой такой точке (или отрезку) сопоставим 0 или 1 в зависимости от того, как расположены входящее
ивыходящее звенья ломаной C по отношению к лучу l: если они расположены по одну сторону от l (или если луч l касается C), то сопоставим 0,

20 Глава I. Графы
а если по разные стороны – сопоставим 1. Чётность (остаток от деления на 2) суммы всех сопоставленных чисел при повороте луча изменяется непрерывно, поэтому чётность постоянна. Ясно также, что во всех точках связной области множества R2 \ C чётность должна быть одной и той же. С другой стороны, если некоторый отрезок пересекает ломаную C ровно в одной точке, то в его концах чётность принимает разные зна-
чения. |
2 |
С л е д с т в и е. Пусть a, b, c, d – точки замкнутой несамопересекающейся ломаной C, расположенные в указанном порядке. Предположим, что точки a и c соединены ломаной L1, а точки b и d соединены ломаной L2, причём обе эти ломаные лежат в одной и той же из двух областей, образованных ломаной C. Тогда ломаные L1 и L2 пересекаются в некоторой точке.
Д о к а з а т е л ь с т в о. Точки a и c разбивают ломаную C на две части. Ломаные C и L1 разбивают плоскость на три области: границей одной из этих областей служит C, а границами двух других областей служит L1 и дуги ломаной C (для доказательства этого утверждения можно рассмотреть концы отрезка, пересекающего ломаную L1 в одной точке и не пересекающего ломаную C). По условию ломаная L2 лежит в той же области множества R2 \ C, что и ломаная L1. Поэтому точки ломаной L2, близкие к точкам b и d, лежат в разных областях, образо-
ванных ломаными C и L1. |
2 |
Простейшими примерами непланарных графов служат графы K3,3 и K5, изображённые на рис. 5 (вершинами этих графов являются только выделенные точки: у графа K3,3 шесть вершин, а у графа K5 пять вершин). Аналогично можно определить графы Kn и Kn,m. Граф Kn (полный граф с n вершинами) состоит из n вершин, попарно соединённых рёбрами. Граф Kn,m состоит из n + m вершин, разбитых на два подмножества из n вершин и из m вершин; рёбрами соединены все пары вершин из разных множеств.
|
|
Рис. 5. Графы K3,3 и K5
