
топология / Прасолов В. В., Элементы комбинаторной и дифференциальной топологии
.pdf§ 11. |
Двумерные поверхности |
|
|
|
|
|
|
|
|
|
161 |
|||||
во втором случае |
v˜ − e˜ + f˜ |
= v − e + f + 1. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
(2) |
|||||||||
|
обоих случаях величина 2 |
− |
v + e |
− |
f уменьшается при переходе от M2 |
|||||||||||
В h2 |
|
|
|
|
|
|
|
|
|
|
2 |
следует, что для |
||||
к M |
, поэтому из минимальности этой величины для M |
|
||||||||||||||
h |
2 |
утверждение теоремы верно, а значит, |
|
|
|
|
|
|||||||||
M |
|
|
|
|
|
|
||||||||||
|
|
|
h |
2 |
|
0 |
|
2 |
или |
h2 |
0 |
2 |
. |
|
(3) |
|
|
|
|
M |
|
≈ m T |
|
M |
≈ n P |
|
|
||||||
Поверхность M2 получается из Mh2 достаточно простым преобразованием. В первом случае M2 ≈ Mh2 # T 2 или M2 ≈ Mh2 # K2 (приклеивается либо ручка, либо перекрученная ручка). Во втором случае M2 ≈ Mh2 # P2. Во всех случаях
|
|
|
M2 ≈ mT 2 или |
M2 ≈ nP2. |
|
h2) = 2 |
|
|
|
(4) |
||
Легко0 |
проверить,0 |
|
χ |
h2 = |
0 |
χ |
− |
n0 (здесь |
||||
что если |
|
(M ) |
2 − 2m или |
|
(M 2 |
|
2m или |
|||||
числа m |
|
и n определяются равенством (3)), то χ(M ) = 2 |
− |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
||
χ(M ) = |
2 − n (здесь числа m и n определяются равенством |
(4)). Для |
||||||||||
этого нужно воспользоваться равенствами (1) и (2), а также тем, что
h2 |
2 |
h2 |
2 |
h2 |
h2 |
2 |
h2 |
2 |
χ(M |
# T ) = χ(M |
# K ) = χ(M ) − 2 и χ(M |
# P ) = χ(M ) − 1. |
|||||
11.3.Завершение классификации двумерных поверхностей
Чтобы завершить классификацию замкнутых двумерных поверхно-
стей, остаётся доказать следующее утверждение. |
|
|
|||
Т е о р е м а |
11.5. |
Поверхности S2, mT 2, m = 1, 2, . . . , |
и nP2, n = |
||
= 1, 2, . . . , попарно не гомеоморфны. |
|
|
|||
Д о к а з а т е л ь с т в о. |
Пусть M12 и M22 – замкнутые |
двумерные |
|||
поверхности, h: M2 |
M2 |
гомеоморфизм. Покажем, что в таком слу |
- |
||
2 |
2 1 → |
2 – |
|
|
|
чае χ(M1) = χ(M2). |
|
|
|
|
|
На M22 есть два графа, а именно, граф G2, образованный рёбрами M22,
играф G1 – образ графа, состоящего из рёбер M21. Пусть v1, e1 и f1 – число вершин, рёбер и граней для графа G1 на поверхности M22; v2, e2 и f2 – аналогичные числа для графа G2. Оставляя эти числа неизменными, граф G1 можно изменить так, чтобы он стал кусочно-линейным
иего рёбра трансверсально пересекали рёбра графа G2. Рассмотрим граф
G = G1 G2. Пусть v, e и f – число вершин, рёбер и граней для графа G на поверхности M22. Покажем, что v − e + f = v2 − e2 + f2. Рассмотрим для этого произвольную грань графа G2 (т. е. 2-симплекс псевдомногообразия M22). Пусть vα, eα и fα – число вершин, рёбер и граней графа G, принадлежащих этой грани. Согласно формуле Эйлера vα − eα + fα = 1 (в формуле Эйлера вместо 1 стоит 2, но в ней учитывается ещё и неограниченная область, которая в нашем случае отсутствует). Запишем vα
162 |
Глава IV. Двумерные поверхности. Накрытия. Расслоения... |
||||||||||
и e |
в виде v |
α |
= v0 |
+ v00 |
и e |
α |
= e0 |
+ e00 |
, где v0 |
и e0 |
– число вершин |
α |
|
α |
α |
|
α |
α |
α |
α |
|
||
ирёбер, принадлежащих краю рассматриваемой грани, vα00 и eα00 – число внутренних вершин и рёбер. Ясно, что vα0 = eα0 , поэтому vα00 − eα00 + fα = 1. Это означает, что если мы уничтожим все внутренние вершины, рёбра
играни, то эйлерова характеристика не изменится. А из равенства vα0 = eα0 следует, что можно также уничтожить все вершины, лежащие на рёбрах
графа G2; эйлерова характеристика при этом тоже не изменится. Таким образом, v − e + f = v2 − e2 + f2. Граф G можно рассматривать и как
|
2 |
поэтому v |
− |
e + f = v |
1 − |
e |
+ f |
, а значит, |
граф на |
поверхности M1, |
2 |
2 |
1 |
1 |
|
||
v1 − e1 + f1 = v2 − e2 + f2, т. е. χ(M1) = χ(M2). |
|
|
|
|
||||
Итак, |
эйлерова характеристика двумерной поверхности не зависит |
|||||||
от выбора триангуляции, поэтому можно рассмотреть простейшие три-
ангуляции и убедиться, что |
χ(S2) = 2, |
χ(T 2) = 0 и χ(P2) = 1. Легко |
||||||||||||
также2 |
проверить, |
что |
χ2(M2 # N2) = χ(M2) + χ(N2) − 2. |
Следовательно, |
||||||||||
χ |
(mT ) |
= |
2 − 2m и |
χ |
(nP ) |
= |
n. Одинаковые эйлеровы характеристи |
- |
||||||
|
|
|
|
2 − 2 |
|
2 |
|
|
||||||
ки имеют лишь поверхности mT |
и 2mP |
. Поэтому остаётся доказать, |
||||||||||||
что эти поверхности не гомеоморфны (при m > 1).
Поверхности S2 и T 2 с простейшими триангуляциями являются ориентируемыми псевдомногообразиями, поэтому поверхность mT 2 с неко-
торой |
триангуляцией является ориентируемым псевдомногообразием. |
||||
|
|
|
|
|
С другой стороны, поверхность P2 с простей- |
|
|
|
|
шей триангуляцией является неориентируемым |
|
|
|
|
|
|
|
|
|
|
псевдомногообразием. А именно, на поверхно- |
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
сти P2 есть замкнутый путь abca, изображён- |
|
|
|
|
|
|
ный на рис. 69 пунктиром, при обходе вдоль |
|
|
|
|
|
которого изменяется ориентация (2-симплек- |
|
|
|
сы с общей стороной 23 приобрели несогла- |
||
|
|
|
|
|
|
|
|
|
|
|
сованные ориентации). На поверхности nP2, |
|
|
|
n > 1, с некоторой триангуляцией есть такой |
||
|
|
|
|
|
|
же замкнутый путь (состоящий из 6 звеньев),
трансверсально пересекающий рёбра 6 симплексов и изменяющий ориентацию. Это озна-
Рис. 69. Путь на проек- |
чает, что nP2 (n > 1) – неориентируемое псев- |
тивной плоскости, ме- |
домногообразие. |
няющий ориентацию |
Остаётся лишь проверить, что понятие |
|
|
|
ориентируемости двумерной поверхности ин- |
вариантно относительно гомеоморфизмов, т. е. понятие ориентируемости двумерной поверхности можно определить, не обращаясь к триангуляциям.
Пусть M2 – замкнутая двумерная поверхность, γ : I = [0, 1] → M2 – некоторый путь. Покроем M2 открытыми множествами Ui , гомеоморф-

§ 11. Двумерные поверхности |
163 |
ными R2. Задав ориентацию в одной точке x Ui , мы задаём тем самым ориентацию во всех точках множества Ui; под ориентацией мы здесь подразумеваем направление обхода вокруг точки x.
Связные компоненты множеств γ−1 (Ui) образуют открытое покрытие компактного множества I. Выберем из этого покрытия конечное подпокрытие W1, . . . , Wn. Мы будем предполагать, что 0 W1, Wj ∩ Wj+1 6= и 1 Wn. Если в точке x γ (Wj) задана ориентация, то эту ориентацию можно распространить на все точки множества γ (Wj). Учитывая, что γ (Wj) ∩ γ (Wj+1) 6= , эту ориентацию можно распространить и на все точки множества γ (Wj+1). Так можно перенести вдоль пути γ ориентацию из точки γ (0) в точку γ (1). Результат переноса не зависит от того, какое именно конечное подпокрытие мы выбираем из покрытия {γ−1 (Ui)}. Действительно, отождествим одну из областей Ui с R2 и рассмотрим часть кривой γ, расположенную в Ui = R2. Множество Uj ∩ Ui представляет собой открытое подмножество в R2. Перенос ориентации вдоль связной компоненты множества γ ∩ (Uj ∩ Ui) при посредстве Uj даёт тот же самый результат, что и перенос ориентации вдоль γ в R2.
Назовём двумерную поверхность M2 ориентируемой, если перенос ориентации вдоль любого замкнутого пути не изменяет ориентацию, т. е. перенесённая вдоль замкнутого пути ориентация совпадает с исходной. Ясно, что псевдомногообразие, гомеоморфное двумерной поверхности, ориентируемо тогда и только тогда, когда ориентируема эта поверхность. Это означает, в частности, что неориентируемое псевдомногообразие nP2 не может быть гомеоморфно ориентируемому
псевдомногообразию mT 2. |
2 |
У п р а ж н е н и е 2. Докажите, что поверхности nT 2 |
и mP2 можно |
получить из 4n-угольника и 2m-угольника, отождествляя их стороны так, как показано на рис. 70.
З а д а ч а 11.1. а) Докажите, что на поверхности nP2 существует замкнутая кривая γ, после разрезания вдоль которой поверхность становится ориентируемой.
|
− |
|
|
|
|
− |
|
|
|
|
|
||
− |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
|
|
|
|
|||
|
|
|
|
|
Рис. 70. Склеивание поверхностей из многоугольников
164 Глава IV. Двумерные поверхности. Накрытия. Расслоения...
б) Докажите, что если n чётно, то окрестность кривой γ гомеоморфна цилиндру, а если n нечётно – то листу Мёбиуса.
З а д а ч а 11.2. Пусть M21 и M22 – негомеоморфные двумерные поверхности с краем. Могут ли пространства M22 × I и M21 × I быть гомеоморфными?
11.4.Риманово определение рода поверхности
Риман определял род замкнутой ориентируемой двумерной поверхности M2 следующим образом. Предположим, что на поверхности M2 можно расположить p несамопересекающихся замкнутых кривых C1, . . . , Cp так, чтобы они попарно не пересекались и множество M2 \ (C1 ∩ . . . ∩ Cp) было связно, но любые p + 1 такие кривые разбивают M2 на части. Тогда род поверхности M2 равен p.
Покажем, что так определённое число p действительно совпадает с родом g поверхности M2. Несложно привести пример, показывающий, что p > g (см. рис. 71). Остаётся доказать, что если на поверхности M2 расположены кривые C1, . . . , Cp, не разбивающие M2 на части, то p 6 g. Проведём разрезы по кривым C1, . . . , Cp. В результате получим связную ориентируемую поверхность, край которой содержит 2p связных компонент. Заклеим каждую компоненту диском. В результате получим
замкнутую ориентируемую поверхность Mh2, эйлерова характеристика которой равна χ(M2) + 2p = 2 − 2g + 2p. Но χ(Mh2) 6 2, поэтому p 6 g.
Рис. 71. Кривые на двумерной поверхности
З а д а ч а 11.3. Докажите, что на замкнутой неориентируемой поверхности nP2 можно расположить n попарно непересекающихся листов Мёбиуса, но нельзя расположить n + 1 попарно непересекающихся листов Мёбиуса.
§ 12. Накрытия
Фундаментальную группу и накрытия мы подробно рассматривали только для одномерных комплексов, но определили их для произволь-

§ 12. Накрытия |
165 |
ных линейно связных топологических пространств. При доказательстве свойств фундаментальной группы и накрытий мы почти нигде не пользовались специальными свойствами одномерных комплексов. Исключение составляют лишь существование и единственность поднятия пути с данным началом и теорема о существовании и единственности накрытия, соответствующего данной подгруппе фундаментальной группы базы.
Для накрытий произвольных линейно связных пространств существование и единственность поднятия пути не столь очевидны, как для накрытий одномерных комплексов, но доказываются достаточно просто. Для каждой точки пути γ нужно выбрать окрестность, участвующую в определении накрытия. Из компактности отрезка следует, что можно выбрать конечное покрытие пути γ такими окрестностями. С помощью этого конечного набора окрестностей и их прообразов можно построить поднятие пути γ с заданным началом. Это поднятие, очевидно, единственно.
Ситуация с накрытиями, соответствующими данной подгруппе фундаментальной группы, сложнее. Приведённая в теореме 2.9 на с. 52 конструкция существенно использует структуру одномерного комплекса. Более того, для пространств общего вида соответствующая теорема неверна; она верна лишь при определённых ограничениях. Прежде чем перейти к формулировке и доказательству этой теоремы, рассмотрим простейший пример – универсальное накрытие замкнутой ориентируемой двумерной поверхности.
12.1.Универсальные накрытия двумерных поверхностей
Напомним,h |
что накрытие p : Xh → X называют универсальным, ес- |
ли π1 (X) = 0. |
|
Тор T 2 можно получить, отождествив точки (x + m, y + n) и (x, y) для всех пар целых чисел m, n. Поэтому универсальное накрытие тора имеет вид p : R2 → T 2.
Универсальное накрытие сферы с g ручками, где g > 2, проще всего построить с помощью геометрии Лобачевского. Рассмотрим на плоскости Лобачевского H2 правильный 4g-угольник с углом 2πg . Пусть G –
группа движений плоскости Лобачевского, порождённая сдвигами, при которых совмещаются пары противоположных сторон рассматриваемого 4g-угольника. Образы 4g-угольника под действием группы G замощают плоскость Лобачевского. Поэтому отображение p : H2 → H2/G ≈ ≈ M2g является универсальным накрытием сферы с g ручками M2g.

166 Глава IV. Двумерные поверхности. Накрытия. Расслоения...
(Необходимые для этой конструкции сведения из геометрии Лобачевского можно найти в книге [18].)
Описание геометрического строения универсального накрытия поверхности M2g без использования геометрии Лобачевского приведено
в[81].
За д а ч а 12.1. а) Докажите, что универсальное накрывающее пространство плоскости R2, из которой выколото несколько точек, гомеоморфно R2.
б) Пусть ij = {(z1, . . . , zn) Cn | zi = zj} и Σ = Cn \ |
ij . Докажи- |
|
S |
|
i6= j |
те, что для Σ универсальное накрывающее пространство гомеоморфно Cn.
12.2.Существование накрывающего пространства с заданной фундаментальной группой
Пусть H – некоторая подгруппа в группе π1 (X, x0). Прежде чем попытаться построить накрытие p : Xh → X, для которого p π1 (Xh, x˜ 0) = H, посмотрим, какими свойствами должно обладать пространство Xh. Пусть γ1 и γ2 – пути в X из точки x0 в точку x, γh1 и γh2 – поднятия этих путей с началом x˜ 0. Пути γh1 и γh2 заканчиваются в одной и той же точке тогда и только тогда, когда класс петли γ1γ2−1 лежит в H.
Это наблюдение приводит к следующей конструкции пространства Xh. Пусть задано линейно связное пространство X с отмеченной точкой x0 X, и в группе π1 (X, x0) задана подгруппа H. Рассмотрим множество всех путей в X с началом в точке x0. Будем считать пути γ1 и γ2 эквивалентными, если класс петли γ1γ2−1 лежит в H. Точками пространства Xh будем считать классы эквивалентных путей; топология в пространстве Xh будет определена чуть позже. Проекция p : Xh → X сопоставляет пути γ его конец.
Из линейной связности пространства X следует, что отображение p сюръективно.
Предложенная конструкция не всегда приводит к желаемому результату. Но если пространство X локально линейно связно и локально односвязно, т. е. для любой точки x X и для любой окрестности U 3 x существует линейно связная односвязная окрестность V U, то эта конструкция даёт нужный результат. В дальнейшем мы будем предполагать, что пространство X локально линейно связно и локально односвязно. Кроме того, под окрестностью точки пространства X будем подразумевать односвязную линейно связную окрестность. Ясно, что такие окрестности образуют базу топологии пространства X.

§ 12. Накрытия |
167 |
Топология пространства Xh. |
Чтобы определить топологию про- |
странства Xh, достаточно задать базу открытых множеств. Пусть точка x˜ Xh и окрестность U X таковы, что px˜ U. Точка x˜ является классом
эквивалентных путей. Пусть |
γ – один |
|
|
|
из путей (с началом в точке x0), ле- |
|
|
|
|
жащих в этом классе. Сопоставим па- |
|
γ |
|
|
ре U, x множество (U, x) Xh, |
состоя- |
|
ω− |
|
щее из классов эквивалентности продол- |
|
|
ω |
|
жений пути γ путями, целиком лежащими |
|
|
|
||
в U. Ясно, что множество (U, x) не за- |
|
|
висит от выбора пути γ. Кроме того, это |
γ |
|
множество не зависит от выбора точки x˜ |
||
|
в следующем смысле: если x˜ 2 (U, x˜ 1), то (U, x˜ 2) = (U, x˜ 1). Чтобы доказать это, рассмотрим точки x1 = px˜ 1 и x2 = px˜ 2. Соединим точки x1 и x2 путём ω, лежащим
в U (рис. 72). Предположим, что γ1γ – продолжение пути γ1, соединяющего x1 с x0, некоторым путём γ, лежащим в U. Ему можно сопоставить путь γ1ωω−1γ, который является продолжением пути γ1ω, соединяющего x0 с x2, путём ω−1γ, лежащим в U. Пути γ1γ и γ1ωω−1γ гомотопны, поэтому сопоставление γ1γ 7→γ1ωω−1γ задаёт взаимно однозначное со-
ответствие между (U, x˜ 1) и (U, x˜ 2).
В качестве базы топологии пространства Xh выберем все множества вида (U, x˜ ). Нужно проверить, что непустое пересечение двух множеств
базыhсодержит непустоеh |
множество базы. Предположим,h |
что x˜ |
h h |
, |
|
U ∩ V |
|||||
гдеh Uh= (Uh |
, x˜ 1h) и V = (V , x˜ 2). Пусть W = U ∩ V и W = (W , x˜ ). Тогда |
||||
W = U ∩ V |
и W – множество базы. |
|
|
|
|
Непрерывность проекции p. Прообраз окрестности U (связной и односвязной) состоит из набора базисных открытых множеств, поэтому он открыт.
Линейная связность пространства Xh. Пусть x˜ – произвольная точка пространства Xh, т. е. некоторый класс эквивалентных путей. Выберем в этом классе эквивалентности произвольный путь γ (t) в пространстве X. Рассмотрим семейство путей γs (t) = γ (st), где 0 6 s, t 6 1. Пути γs соответствует некоторая точка x˜ (s) Xh. В результате получаем путь в пространстве Xh, соединяющий точки x˜ (0) = x˜ 0 и x˜ (1) = x˜ .
Проекция – локальный гомеоморфизм. Пусть p : (U, x˜ ) → U –
ограничение отображения p на множество (U, x˜ ), где U – связная

168 |
Глава IV. Двумерные поверхности. Накрытия. Расслоения... |
односвязная окрестность. Линейная связность U влечёт сюръективность отображения p, а односвязность U влечет инъективность отображения p. Чтобы доказать непрерывность отображения p, рассмотрим произвольную связную односвязную окрестность V U. Прообразом этой окрестности является открытое множество (U, x˜ ).
Образ группы πi (Xh, x˜ 0) при отображении p совпадает с H.
Пусть γ – петля в X с началом и концом в точке x0, γh – поднятие этой петли с началом в точке x˜ 0. Подгруппа p π1 (Xh, x˜ 0) состоит из гомотопических классов тех петель γ, для которых путь γh замкнут. По построению путь γh замкнут тогда и только тогда, когда класс эквивалентности пути γ соответствует точке x˜ 0, т. е. гомотопический класс петли γ лежит в H.
12.3.Единственность накрывающего пространства с заданной фундаментальной группой
Для доказательства единственности накрывающего |
пространства |
с заданной группой p π1 (Xh, x˜ 0) π1 (X, x0) не нужна |
локальная од- |
носвязность пространства X; нужна лишь его локальная линейная связ- |
|
ность. Доказательство единственности опирается на следующую лемму. Л е м м а. Пусть q : Y˜ → Y – накрытие, f : X → Y – некоторое (непрерывное) отображение, причём пространство X линейно связно и локально линейно связно. Тогда если f π1 (X, x0) q π1 (Y˜ , y˜ 0), то существует единственное поднятие f˜ : X → Y отображения f
(имеется в виду, что q f˜ |
= f и f˜ (x0) = y˜ 0). |
Д о к а з а т е л ь с т в о. |
Рассмотрим произвольный путь γ в про- |
странстве X, соединяющий точку x0 с некоторой точкой x. При отображении f он переходит в путь fγ. Пусть γh – поднятие пути fγ с началом в точке y˜ 0. Положим f˜ (x) = y˜ , где y˜ – конец пути γh. Нужно проверить, что y˜ не зависит от выбора пути γ. Иными словами, если γ1 и γ2 – пути из x0 в x, а ω – петля, составленная из путей γ1 и γ2, то поднятие петли fω с началом y˜ 0 должно быть замкнутым путём в Y˜ . Это означает, что класс петли fω должен лежать в q π1 (Y˜ , y˜ 0). Иными словами, f π1 (X, x0) q π1 (Y˜ , y˜ 0). Это выполняется по условию.
Остается доказать непрерывность отображения f˜ . Для этого нам понадобится локальная линейная связность пространства X. Пусть x X и y˜ = f˜ (x). Для точки y = q(y˜ ) выберем линейно связную окрестность U, участвующую в определении накрытия. Пусть Uh – линейно связная компонента множества p−1 (U), содержащая точку y˜ . Из непрерывности отображения f следует, что f−1 (U) содержит некоторую окрестность V точки x. Пространство X локально линейно связно, поэтому можно
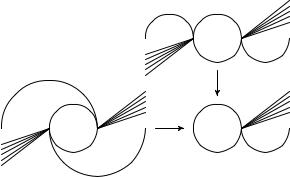
§ 12. Накрытия |
|
|
|
169 |
||
что окрестность V линейно связна. В таком случае |
˜ |
|
h |
|||
f (V) |
|
U, |
||||
считать, ˜ −1 |
h |
V |
|
|
|
|
т. е. V f |
(U). В самом деле, любую точку x1 |
можно соединить |
||||
с точкой x путём γ, лежащим в V . Образ fγ пути γ лежит в U, поэтому
путь |
|
|
h |
fγ поднимается до пути, целиком лежащего в U. Это означает, что |
|||
˜ |
= y˜ |
h |
2 |
f (y) |
U. |
||
С помощью этой леммы легко доказать единственность накрывающего пространства с заданной фундаментальной группой. А именно, пусть pi : Xhi → X (i = 1, 2) – накрытия линейно связного и локально линейно
связного пространства X, причём (p1) π1 (Xh1, x˜ 1) (p2) π1 (Xh2, x˜ 2). Тогда существует такой гомеоморфизм h: Xh1 → Xh2, что p2h = p1 и h(x˜ 1) = x˜ 2.
Отображение h строится как поднятие отображения p1, а отображение h−1 строится как поднятие отображения p2.
Из доказательства леммы видно, что поднятие f˜ существует и единственно для любого линейно связного пространства X. Но если X не является локально линейно связным, то отображение f˜ не обязательно непрерывно. Это показывает следующий пример.
П р и м е р (Зиман). Пусть топологическое пространство X R2 состоит из окружности, дуги AB и бесконечного набора отрезков I1, I2, . . . , один конец которых находится в точке A, а другой конец стремится к точке B (рис. 73). Топологические пространства Xh1 и Xh2 устроены так, как показано на том же рисунке. Накрытия pi : Xhi → X устроены следующим образом. Окружность пространства Xhi дважды обматывается вокруг окружности пространства X, отрезки отображаются изометрично, а дуги отображаются гомеоморфно. Тогда
(p1) π1 (Xh1) = (p2) π1 (Xh2) = 2Z Z = π1 (X),
но у отображения p1 нет непрерывного поднятия h, для которого p2h= p1.
|
|
|
h |
|
|
|
|
|
|
|
h |
|
|
Рис. 73. Пример Зимана

170Глава IV. Двумерные поверхности. Накрытия. Расслоения...
Всамом деле, поднятие h существует и единственно (если задан образ
одной точки при отображении h), но отображение h разрывно в точках P и Q, лежащих в p1−1 (B).
З а д а ч а 12.2. Докажите, что mn-листное накрытие p : Xh → X можно представить в виде композиции
Xh −p→1 Y −p→2 X,
где p1 – некоторое m-листное накрытие и p2 – некоторое n-листное накрытие, тогда и только тогда, когда прообраз p−1 (x) некоторой точки x X можно разбить на m-элементные множества I1, . . . , In так, что для любого замкнутого пути в X все его поднятия, начинающиеся в одном и том же множестве Ii , заканчиваются в одном и том же множестве Ij .
Используя технику накрытий, с помощью теоремы Борсука–Улама можно доказать следующее утверждение, из которого сама теорема Бор- сука–Улама легко выводится.
Т е о р е м а 12.1. Пусть m > n > 1. Тогда не существует отоб-
ражения |
g : RPm → RPn, |
индуцирующего изоморфизм фундамен- |
||||||||||||||||||
тальных групп. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Д о к а з а т е л ь с т в о. |
Пусть |
|
p |
m |
: Sm |
→ |
RPm и pn : Sn |
→ |
RPn – |
|||||||||||
|
|
|
|
|
|
|
|
|
|
f : S |
m |
|
S |
n |
|
|
|
|||
двулистные накрытия. Построим |
отображение |
|
→ |
|
, для которого |
|||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|||||||
gpm = p |
n |
f. Фиксируем точку x |
0 |
|
S |
|
, выберем из двух точек множества |
|||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
x S |
m |
путём γ, |
||||||
pn |
g(x0) |
одну точку y0, соединим точку x0 с точкой |
|
|||||||||||||||||
рассмотрим поднятие пути |
gpmγ |
с |
началом |
y0 и |
положим |
g(x) = y, |
||||||||||||||
где y – конец этого поднятия. Корректность этого определения следует из того, что в Sm любая петля стягиваема, поскольку m > 2.
Из равенства gpm = pn f следует, что f(−x) = ±f(x). Знак выясняется следующим образом. Пусть αm и αn – образующие групп π1 (RPm) и π1 (RPn) (здесь мы пользуемся тем, что π1 (RP1) = Z и π1 (RPm) = Z2
при m |
|
2). Пусть, далее, g |
km |
|
k n (здесь k Z2 |
при n |
|
|
2 и k Z |
||||||||
|
> |
|
α |
|
= |
α |
|
|
|
|
|
|
> |
|
|
|
|
при n = 1). Тогда f(−x) = (−1) |
f(x), поскольку kαn – образ дуги, соеди- |
||||||||||||||||
няющей точки x и −x, при отображении gpm. |
m |
|
n |
|
|
|
|
|
|
||||||||
Итак, если существует отображение g : RP |
|
m→ RPn |
|
, для |
которого |
||||||||||||
g αm = ±αn, то существует |
отображение f : S |
→ S |
|
, |
для |
|
которого |
||||||||||
f(−x) = −f(x). |
|
|
|
|
|
|
m |
|
|
n |
|
|
|
2 |
|||
Отметим, что если существует отображение f : S |
|
→ S , |
для кото |
||||||||||||||
|
|
m |
→ RP |
n- |
|||||||||||||
рого f(−x) = −f(x), то можно рассмотреть отображение g : RP |
|
, |
|||||||||||||||
заданное формулой {x, −x} 7→{f(x), −f(x)}. Для этого отображения выполняется равенство g αm = kαn, где k нечётно. Если n > 2, то αn Z2, поэтому g – изоморфизм. Если же n = 1, то g является ненулевым
