
топология / Прасолов В. В., Элементы комбинаторной и дифференциальной топологии
.pdf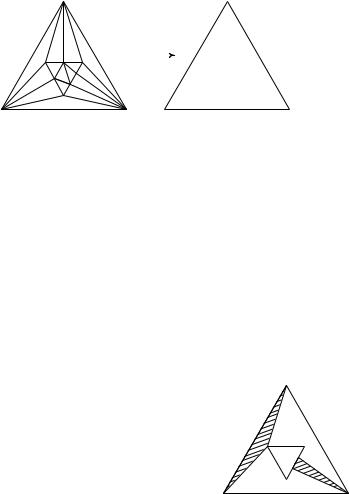
§ 8. Симплициальные комплексы |
|
|
121 |
|||
|
|
|
|
|
|
|
|
|
|
ψ |
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|||||
|
Рис. 44. Построение комплекса K1 |
|
||||
Д о к а з а т е л ь с т в о. Пусть |
v0, v1, . . . , vn – вершины симплек- |
|||||
са L, m – его центр масс, точка ai |
выбрана так, что m лежит на отрезке |
|||||
[ai , vi] и |aim| = k|mvi|, где k > 0 – фиксированное число. Если k достаточно велико, то симплекс L = [v0, . . . , vn] лежит внутри симплек-
са [a0, . . . , an].
Рассмотрим симплициальный комплекс K1, вершинами которого являются точки a0, . . . , an и вершины комплекса K (напомним, что K – триангуляция L); симплексами K1 являются симплексы K и симплексы, одной из вершин которых служит ai, а остальными вершинами служат вершины симплекса из K, расположенного на грани [v0, . . . , vˆ i, . . . , vn].
Пример построения комплекса K1 при n = 2 приведён на рис. 44. Определим симплициальное отображение ψ : K1 → L так, чтобы оно совпадало с ϕ на K K1 и переводило ai в vi. Поме-
тим каждую вершину a комплекса K1, сопо- |
|
|
|
|
ставив ей номер i вершины vi = ψ (a). Такой |
|
|
|
|
набор пометок удовлетворяет лемме Шпер- |
|
|
|
|
нера, поэтому ψn = 1. Остаётся доказать, что |
|
|
|
|
ψn = ϕ0 − ϕ1 + ϕ2 − . . . + (−1)nϕn. |
|
|||
Рассмотрим сначала для наглядности слу- |
|
|
|
|
чай n = 2 (рис. 45). Каждой вершине vi K1, |
|
|
|
|
помеченной числом i, соответствует симплекс |
|
|
||
[vi , aj, ak] в K1 с полным набором пометок. |
|
|||
Рис. 45. Ориентации сим- |
||||
Этот симплекс ориентирован положительно |
||||
(т. е. так же, как и симплекс [a0, a1, a2]). Если |
плексов |
|
|
|
одномерный симплекс [x, y] в K1 с пометками p и q даёт вклад в ϕ1, то он по условию лежит на отрезке [vp, vq]. Ребру [x, y] соответствует симплекс [x, y, ar], r 6= p, q, с полным набором пометок. Ориентация этого симплекса противоположна ориентации ребра [x, y] на ребре [vp, vq], потому что ориентации симплексов [a0, a1] и [v0, v1] противоположны (эти симплексы расположены на параллельных прямых, поэтому име-
122 |
Глава III. Топологические пространства |
ет смысл говорить о согласованности их ориентаций). Наконец, если симплекс [x, y, z] в K1 даёт вклад в ϕ2, то он имеет полный набор пометок. При этом ориентации симплекса [x, y, z] относительно [v0, v1, v2]
иотносительно [a0, a1, a2] совпадают, поскольку симплексы [v0, v1, v2]
и[a0, a1, a2] одинаково ориентированы.
Для произвольного n рассуждения аналогичны. Чередование знаков
происходит из-за того, что симплексы [vi0 , vi1 , . . . , vik ] и [ai0 , ai1 , . . . , aik ] одинаково ориентированы при чётном k и противоположно ориентирова-
ны при нечётном k. |
2 |
8.5.Нерв покрытия
Произвольному семейству подмножеств U = {Uα } множества X можно сопоставить симплициальный комплекс N = N(U), вершины {vα} которого находятся во взаимно однозначном соответствии с множествами {Uα }, причём набор vα0 , . . . , vαk является симплексом тогда и только тогда, когда Uα0 ∩ . . . ∩ Uαk 6= . Если X – топологическое пространство и U – его покрытие (не обязательно открытое), то N называют нервом покрытия U.
П р и м е р. Пусть K – симплициальный комплекс с вершинами {vα}, Uα = st vα – звезда вершины vα, т. е. объединение внутренностей всех симплексов, содержащих vα. Тогда нерв покрытия {Uα } совпадает с K.
Д о к а з а т е л ь с т в о. Вершины vα0 , . . . , vαk образуют симплекс
k тогда и только тогда, когда st vα0 ∩ . . . ∩ st vαk = st k 6= . |
2 |
Будем называть открытое покрытие U пространства X стягивае- |
|
мым, если все непустые конечные пересечения Uα0 ∩ . . . ∩ Uαk |
стягива- |
емы. Нерв стягиваемого покрытия несёт много информации о гомотопическом строении пространства X. Например, справедливо следующее утверждение.
Т е о р е м а 8.10. Пусть U = {Uα } – стягиваемое локально конечное покрытие паракомпактного пространства X. Тогда нерв
N= N(U) гомотопически эквивалентен X.
До к а з а т е л ь с т в о. Стягиваемость покрытия и паракомпактность пространства используются в разных местах доказательства. Поэтому будем считать, что U – произвольное локально конечное открытое покрытие произвольного пространства X. Построим вспомогательное пространство XU следующим образом. Для каждого непустого
пересечения |
Uα0 |
. . . |
∩ |
Uαn |
= Uα0 ...αn рассмотрим прямое произведе- |
|||
ние |
Uα0...αn × |
n ∩ |
|
где |
n |
вершинами α0, . . . , |
||
α0...αn , |
|
α0...αn – симплекс с |
||||||
αn. |
Затем |
в |
дизъюнктном |
объединении таких |
топологических про- |
|||
странств произведём следующую склейку: отождествим точку (x, y), где
§ 8. Симплициальные комплексы |
|
|
123 |
||||
x Uα0...αn |
и y [α0 . |
. . αˆ i |
. . . αn] |
αn |
0 |
...αn , с соответствующей точкой |
|
пространства Uα0 αˆ i |
αn × |
n−1 |
; |
|
здесь мы пользуемся тем, что |
||
α0...αˆ i ...αn |
|
||||||
Uα0 ...αn Uα0 |
...αˆ i ...αn . |
|
|
|
|
|
|
Ш а г 1. |
Если пространство X паракомпактно, то X XU . |
||||||
Пусть |
p : XU → X –nотображение, |
|
индуцированное естественными |
||||
проекциями Uα0...αn × |
α0... |
αn → Uα0... |
αn . Это отображение непрерывно, |
||||
поскольку покрытие U открытое. Каждую точку множества p−1 (x) можно записать в виде суммы P tαxα , где tα > 0, P tα = 1 и xα = x для Uα 3 x.
α
Эта сумма конечная, поскольку покрытие локально конечное.
Из паракомпактности пространства X следует, что существует разби-
ение единицы {ϕα }, подчинённое покрытию {Uα }, т. е. supp ϕα Uα . Построим отображение s : X → XU следующим образом: s(x) = P ϕα (x)xα ; здесь имеется в виду, что если ϕα (x) = 0, то соответствующее слагаемое нулевое, а если ϕα (x) 6= 0, то x Uα и мы полагаем xα = x. Ясно, что p ◦ s = idX . Нужно лишь проверить, что s ◦ p idXU . Пусть точка x принадлежит множествам Uα0 , . . . , Uαn и не принадлежит никаким другим множествам Uα . Тогда точки y = P tαxα и s p(y) = P ϕαxα принадлежат симплексу с вершинами xα0 , . . . , xαn . Требуемая гомотопия строится следующим образом: мы соединяем точки y и s p(y) отрезком и равномерно подтягиваем точку s p(y) к точке y.
Ш а г 2. Если покрытие U стягиваемое, то XU |N(U)|.
Возьмём пространство XU . Сначала над каждой вершиной α стянем в точку множество Uα, затем над каждой внутренней точкой ребра [α, β] стянем в точку множество Uα,β , затем над каждой внутренней точкой симплекса [α, β, γ] стянем в точку множество Uα,β,γ и т. д. В итоге получим
пространство |N(U)|. |
2 |
8.6.Псевдомногообразия
Конечный симплициальный комплекс K называют n-мерным псевдомногообразием, если выполняются следующие условия:
–однородность: каждый симплекс из K является гранью некоторого n-мерного симплекса ;
–неразветвлённость: каждый (n − 1)-мерный симплекс из K является гранью не более чем двух n-мерных симплексов ;
– сильная связность: для любых двух n-мерных симплексов |
an и |
||||||||||||
n найдётся последовательность симплексов |
n = |
n |
, |
n, . . . , |
n = |
n, |
|||||||
b |
|
|
|
|
n |
|
n |
1 |
a |
|
2 |
k |
b |
в которой соседние члены |
|
|
|
|
− 1)-мерную грань. |
||||||||
|
i и |
i+1 имеют общую (n |
|||||||||||
Объединение всех |
(n |
− |
1) |
- |
мерных симплексов n мерного псевдом |
||||||||
ногообразия M |
n |
|
|
|
|
|
- |
|
|
- |
|||
|
, которые |
являются гранью |
ровно |
одного n-мерного |
|||||||||

124 Глава III. Топологические пространства
симплекса, называют краем и обозначают ∂Mn. Если ∂Mn = , то псевдомногообразие Mn называют замкнутым. В замкнутом псевдомногообразии Mn любой (n − 1)-мерный симплекс является гранью ровно
двух n-мерных симплексов. |
симплекса |
n |
|
n |
семейство всех одинако |
|||
Назовём ориентацией |
|
n |
|
|
R |
|
|
n- |
во ориентированных реперов в R |
|
с началами в точках симплекса |
. |
|||||
При n > 0 каждый симплекс имеет ровно две ориентации. Если симплекс снабжён ориентацией, то эту ориентацию называют положительной,
а противоположную ориентацию называют отрицательной. |
n−1 |
|
|
|||||||||||||
|
Ориентация симплекса |
|
n индуцирует ориентацию его грани |
|
||||||||||||
|
|
n |
следующим образом. Выберем в |
точке x |
n−1 |
|
|
|||||||||
|
|
|
положительно |
|||||||||||||
ориентированный репер, |
первые |
n |
− |
1 |
векторов которого принадле |
- |
||||||||||
жат |
|
n−1 |
, а |
последний |
вектор |
|
|
|
n |
|
|
|
||||
|
|
направлен внутрь |
|
. Ориентацию, |
||||||||||||
заданную |
в |
n−1 первыми |
n − 1 |
векторами, будем |
считать положи- |
|||||||||||
тельной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Псевдомногообразие Mn |
называют ориентируемым, если во всех |
||||||||||||||
его n-мерных симплексах можно выбрать ориентацию так, что любые два симплекса, имеющие общую (n − 1)-мерную грань, индуцируют на ней противоположные ориентации. Из условия сильной связности следует, что если псевдомногообразие ориентируемо, то его ориентацию можно выбрать ровно двумя способами. Ориентируемое псевдомногообразие Mn
сфиксированной ориентацией называют ориентированным.
Пр и м е р. Представим лист Мёбиуса в виде абстрактного симплициального комплекса с шестью вершинами (рис. 46). Реализовав этот абстрактный симплициальный комплекс в R5 (это можно сделать согласно теореме 8.4 на с. 116), получим неориентируемое псевдомногообразие.
П р и м е р. Пусть |
Mn |
1 |
Rm – псевдомногообразие |
(возможно, с |
||||||||||
краем). Вложим m в |
|
m |
и |
выберем в |
Rm |
|
1 |
|
Rm |
точку a. Объ |
- |
|||
|
R |
R |
|
+ |
|
|
|
|
+ |
|
\ |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||
единение всех отрезков вида [a, x], где x M |
|
, является (nn + 1)-мерным |
||||||||||||
псевдомногообразием. Его называют надстройкой над M и обозначают |
||||||||||||||
ΣMn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 46. Триангуляция листа Мёбиуса

§ 8. Симплициальные комплексы |
125 |
З а м е ч а н и е. Надстройка над обычным (топологическим или гладким) замкнутым многообразием Mn может быть многообразием лишь в том случае, когда Mn – гомологическая сфера. Таким образом, псев-
домногообразия |
образуют более |
широкий |
класс, чем многообразия. |
||||||
С другой стороны, если Mn – псевдомно- |
|
||||||||
гообразие и (Mn)n−2 – его (n |
− |
2)-мерный |
|
||||||
остов, то M |
n |
\ |
n n−2 |
|
|
много- |
|
||
|
(M ) |
|
является |
|
|||||
образием, т. е. псевдомногообразие стано- |
|
||||||||
вится многообразием после выбрасывания |
|
||||||||
множества коразмерности 2. |
|
|
|
|
|||||
П р и м е р. |
Надстройка |
над |
2-мер- |
|
|||||
ным псевдомногообразием, изображенным |
|
||||||||
на рис. 47, является 3-мерным псевдом- |
|
||||||||
ногообразием, |
край |
которого – не |
псев- |
Рис. 47. Край надстройки – |
|||||
домногообразие |
(не выполняется условие |
||||||||
сильной связности). |
|
|
|
|
|
не псевдомногообразие |
|||
8.7.Степень отображения в евклидово пространство
Пусть Mn – псевдомногообразие размерности n. Будем называть отображение f : Mn → Rm симплициальным, если ограничение f на каждый симплекс является линейным отображением (в аффинном смысле). Симплициальное отображение Mn → Rm полностью определяется ограничением на 0-мерный остов (Mn)0, причём любое отображение (Mn)0 → Rm продолжается до симплициального отображения Mn → Rm.
Рассмотрим симплициальное отображение f : Mn → Rn (размерности одинаковые). Назовём точку y Rn регулярным значением отображения f, если точка y не принадлежит образу (n − 1)-мерного остова псевдомногообразия Mn. Регулярные значения образуют в Rn всюду плотное подмножество.
Пусть Mn – ориентированное псевдомногообразие, f : Mn → Rn – симплициальное отображение и y – регулярное значение отображения f. Назовём степенью отображения f относительно точки y число
X
deg(f, y) = sgn Jf (x),
x f−1 (y)
где sgn Jf (x) – знак якобиана отображения f в точке x, т. е. sgn Jf (x) = 1, если симплекс n, внутри которого лежит точка x, отображается на симплекс f( n) Rn с сохранением ориентации; в противном случае sgn Jf (x) = −1.

126 |
Глава III. Топологические пространства |
Т е о р е м а 8.11. |
Пусть Mn – ориентированное псевдомного- |
образие, f : Mn → Rn |
– симплициальное отображение, y1 и y2 – |
регулярные значения отображения f. Тогда если точки y1 и y2 принадлежат одной и той же компоненте связности множества
Rn \ f(∂Mn), то deg(f, y1) = deg(f, y2).
Д о к а з а т е л ь с т в о. Образ (n − 2)-мерного остова псевдомногообразия Mn не разбивает Rn, поскольку (n − 2)-мерное подпространство в Rn не разбивает Rn. Поэтому в Rn существует конечнозвенная ломаная L с концами y1 и y2, которая не пересекает образ (n − 2)-мерного остова, не пересекает f(∂Mn) и пересекает образ (n − 1)-мерного остова лишь в конечном числе точек a1, . . . , ak. Множество f−1 (ai) не содержит точек, принадлежащих симплексам размерности 6 n − 2, поэтому множество f−1 (ai) является объединением конечного числа множеств, каждое из которых либо состоит из одной внутренней точки (n − 1)-мерной грани, либо представляет собой отрезок внутри n-мерной грани, соединяющий внутренние точки двух его (n − 1)-мерных граней.
По условию f−1 (ai) ∩ ∂Mn = , поэтому как внутренней точке (n − 1)-мерного симплекса, так и отрезку внутри n-мерного симплекса соответствуют два n-мерных симплекса. Если образы этих симплексов имеют одинаковые ориентации, то при прохождении через точку ai количество прообразов не изменяется и знаки якобианов в них тоже не изменяются: см. рис. 48 (а); при этом мы имеем в виду только прообразы, принадлежащие двум рассматриваемым симплексам. Если же образы симплексов имеют разные ориентации, то либо возникают, либо исчезают два прообраза с противоположными знаками якобиана
(рис. 48 (б)). Сумма знаков якобианов при этом не изменяется. |
2 |
Т е о р е м а 8.12. Пусть Mn – ориентированное псевдомногообразие, f, g : Mn → Rn – симплициальные отображения, ограничения которых на ∂Mn совпадают. Предположим, что y – регулярное значение отображений f и g. Тогда deg(f, y) = deg(g, y).
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 48. Прохождение через критическое значение

§ 8. Симплициальные комплексы |
|
|
|
|
|
127 |
|
Д о к а з а т е л ь с т в о. |
Рассмотрим |
семейство |
отображений |
ft = |
|||
= (1 −nt) f + tg. Ясно, что |
f0 = f, f1 = g |
и ограничение отображения ft |
|||||
на ∂M не зависит от t. |
|
|
n |
∂ |
n |
содержа |
|
Пусть X – компонента связности множества R |
|
\ ft ( |
M ), |
|
n- |
||
щая точку y (множество X не зависит от t, потому что множество ft (∂M ) не зависит от t). Множество X открытое, поэтому регулярные значения отображения ft образуют в нём всюду плотное подмножество. В частности, каждое отображение ft имеет регулярное значение yt X. Согласно теореме 8.11 deg(ft , yt) не зависит от выбора регулярного значения yt X, поэтому можно определить функцию ϕ(t) = deg(ft , yt).
Для любого регулярного значения yt X отображения |
ft существует |
ε > 0, обладающее следующими свойствами: при всех τ |
(t − ε, t + ε) ∩ |
∩ [0, 1] точка yt является регулярным значением отображения fτ и прообраз fτ−1 (yt) при всех τ состоит из одного и того же числа точек с одними и теми же знаками якобианов. Действительно, если yt – внутренняя точка образа n-мерного симплекса при линейном отображении в Rn, то при малом шевелении линейного отображения точка yt останется внутренней точкой образа. Итак, функция ϕ(t) постоянна на множестве Ut = (t − ε, t + ε) ∩ [0, 1]. Семейство множеств {Ut }, t [0, 1], образует открытое покрытие отрезка [0, 1]. Выбрав из этого покрытия конечное подпокрытие, легко убедиться, что функция ϕ(t) постоянна на всём
отрезке [0, 1], поэтому ϕ(0) = ϕ(1), т. е. deg(f, y1) = deg(f, y0). |
2 |
С помощью теоремы 8.12 легко доказывается лемма Шпернера, причём даже в уточнённой форме (теорема 6.9 на с. 95). Основная идея доказательства ясна уже в случае 2-мерных симплексов, поэтому мы ограничимся этим случаем (подробное доказательство для n-мерных симплексов приведено в [130]). Вложим триангулированный симплекс в больший симплекс и триангулируем этот новый объект (рис. 49). При этом нужно, чтобы не появилось новых симплексов с полными наборами поме-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 49. Дополнительная триангуляция симплекса
128 |
Глава III. Топологические пространства |
ток; этого легко добиться. Большой триангулированный симплекс является ориентированным псевдомногообразием. Рассмотрим симплициальное отображение f этого псевдомногообразия на фиксированный симплекс
вRn с полным набором пометок (вершина с номером i отображается
ввершину с номером i). На крае отображение f совпадает с тождественным отображением, поэтому его степень (относительно внутренней
точки симплекса ) равна 1. Но степень отображения f как раз и равна разности между количествами симплексов с полным набором пометок с положительной и отрицательной ориентациями. А по построению новых симплексов с полным набором пометок не появилось.
8.8.Теорема Борсука–Улама
В1933 г. К. Борсук [38] доказал следующее утверждение, предположение о справедливости которого высказал ранее С. Улам.
Т е о р е м а 8.13 (Борсук–Улам). Пусть f : S |
n |
→ R |
n |
|
n |
||
|
|
|
– непрерыв- |
ное отображение. Тогда f(x) = f(−x) для некоторой точки x S . Точки x и −x называют антиподами, поэтому теорему Борсука–
Улама иногда называют теоремой об антиподах.
Отображение g : Sn → Rn называют нечётным, или антиподаль-
ным, если |
g(−x) = −g(x). Легко видеть, что теорема Борсука–Улама |
||||||||||||||||||||||||||
эквивалентна следующему утверждению. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Т е о р е м а |
8.14. Пусть g : S |
n |
→ R |
n |
|
|
n |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
нечётное отображение. |
||||||||
Тогда g(x) |
= |
0 для |
некоторой точки x |
|
|
S . |
|
|
|
|
|
|
|||||||||||||||
|
если |
f : S |
n |
→ R |
n |
|
|
|
|
|
|
отображение, |
то |
||||||||||||||
Действительно, |
|
|
|
|
– произвольное |
|
|||||||||||||||||||||
отображение g(x) |
= |
f(x) − f(−x) |
нечётно, а |
равенство |
f(x) = f( x) |
эк |
- |
||||||||||||||||||||
|
|
|
|
n |
→ R |
n |
− |
|
|||||||||||||||||||
вивалентно равенству g(x) = 0. Наоборот, если g : S |
|
|
– нечётное |
||||||||||||||||||||||||
отображение и |
теорема Борсука |
|
Улама верна, то g(x) = g( x) для неко |
- |
|||||||||||||||||||||||
|
n |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||||||
торой точки x S |
|
. С другой стороны, g(−x) = −g(x), поэтому g(x) = 0. |
|||||||||||||||||||||||||
Теорему 8.14 мы выведем из следующего утверждения. |
|
|
|
|
|||||||||||||||||||||||
Т е о р е м а |
|
|
|
n−1 |
|
n |
|
|
Dn |
|
→ R |
n – отображение, |
|
|
|
||||||||||||
|
|
|
8.15. Пусть h: |
|
|
|
ограниче- |
||||||||||||||||||||
ние которого на S |
|
|
= ∂D нечётно. Тогда h(x) = 0 для некоторой |
||||||||||||||||||||||||
точки x Dn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
n |
||
Чтобы вывести теорему 8.14 из теоремы 8.15, нужно в качестве |
|
||||||||||||||||||||||||||
взять сечение шара Dn+1 (с краем Sn) плоскостью, проходящей через центр, а в качестве h взять композицию проекции Dn на полусферу
иотображения g.
До к а з а т е л ь с т в о т е о р е м ы 8.15. Вместо Dn мы будем рассматривать n-мерный куб In, где I = [−1, 1]. Этот куб симметричен относительно начала координат. Предположим, что ограничениеотображения
§ 8. Симплициальные комплексы |
129 |
h: In → Rn на ∂In нечётно и 0 6 h(In). Множество h(In) компактно, поэтому оно не пересекается с некоторым шаром с центром 0. Пусть r – радиус этого шара.
Из равномерной непрерывности отображения h следует, что для достаточно мелкой триангуляции куба In образ любого симплекса лежит в шаре диаметра ε < r. Для каждой вершины v такой триангуляции положим hε (v) = h(v) и продолжим отображение hε на каждый симплекс по линейности. Любая точка x In принадлежит какому-то симплексу триангуляции, поэтому точки h(x) и hε (x) принадлежат одному и тому же шару диаметра ε, а значит, kh(x) − hε (x)k 6 ε.
Триангуляцию куба In можно построить так, что она будет симметрична относительно начала координат. В таком случае ограничение отображения hε (x) на ∂In нечётно. Кроме того, из неравенства kh(x) − hε (x)k 6 ε следует, что 0 6 hε (In).
Чтобы прийти к противоречию, достаточно построить симплици-
альное отображение ϕ : In → Rn, |
ограничение которого на ∂In совпа- |
|||||||||||
дает с hε и для которого |
deg(ϕ, 0) – нечётное число. Действительно, |
|||||||||||
с одной стороны |
deg(hε, 0) = 0; |
с другой стороны, по |
теореме |
8.12 |
||||||||
deg(ϕ, 0) = deg(hε, 0). |
|
|
|
|
|
|
|
|
|
|
||
|
ϕ |
|
n |
|
n |
|
|
|
|
регу |
|
|
Ясно, что если |
: I |
|
→ R – нечётное отображение и 0 – его |
- |
||||||||
|
|
−1 |
|
|||||||||
лярное значение, то deg(ϕ, 0) – нечётное число. Действительно, ϕ |
|
(0) |
||||||||||
состоит из точки 0 и пар вида (x, |
− |
x), а чётность суммы |
P ± |
1 зависит |
||||||||
лишь от количества слагаемых. |
|
|
|
|
|
|||||||
Построить нечётное отображение ϕ совсем просто. Нужно взять внутренние вершины симметричной триангуляции, полученной при построении отображения hε, и произвольно отобразить симметричные вершины в симметричные точки Rn. При этом для вершины v ∂In полагаем ϕ(v) = hε (v). Затем продолжаем отображение ϕ по линейности.
Остаётся последняя чисто техническая трудность: точка 0 является вершиной триангуляции, поэтому 0 = ϕ(0) – не регулярное значение. Сделать точку 0 регулярным значением можно следующим образом. Пусть W – объединение всех симплексов с вершиной 0. Можно считать,
что W ∩ ∂In = . Для вершины v W положим ϕ(v) = v. Тогда ϕ|W – тождественное отображение, поэтому оно останется симплициальным при
любой триангуляции множества W . Теперь малым шевелением вершин,
не принадлежащих ∂In, можно добиться того, что точка 0 Rn |
будет |
регулярным значением отображения ϕ. |
2 |
Приведём ещё одно утверждение, эквивалентное теореме Борсука– Улама.
Т е о р е м а 8.16. Пусть m > n > 1. Тогда не существует нечётного отображения f : Sm → Sn.
130 |
Глава III. Топологические пространства |
Действительно, если m > n > 1, то нечётное отображение Sm → Sn является также и нечётным отображением Sm → Sn Rn+1 \ {0} Rm \ {0}. Поэтому из теоремы Борсука–Улама следует теорема 8.16. Наоборот, по нечётному отображению Sm → Rm \ {0} легко построить нечётное отображение Sm → Sm−1.
За м е ч а н и е. Весьма простое доказательство теоремы Борсука– Улама приведено в [95]. Приведённое нами доказательство теоремы 8.15 имеет много общего с [61].
За д а ч а 8.4.* а) (лемма Такера [127]) Пусть задана такая триангуляция n-мерного куба In, что его граница ∂In триангулирована симметрично относительно центра. Предположим, что вершины этой триангуляции помечены числами ±1, ±2, . . . , ±n, причём если v ∂In – вершина триангуляции, то вершины v и −v помечены числами, сумма которых равна 0. Докажите, что тогда существуют смежные (т. е. соединённые ребром) вершины триангуляции, помеченные числами, сумма которых равна 0.
б) Докажите теорему Борсука–Улама с помощью леммы Такера.
За м е ч а н и е. Чисто алгебраическое доказательство теоремы Бор- сука–Улама для полиномиальных отображений приведено в [16].
8.9.Следствия и обобщения теоремы Борсука–Улама
Из теоремы Борсука–Улама можно вывести много интересных следствий. Одно из них Борсук привёл в той самой статье [38], в которой он доказал теорему Борсука–Улама. Но ранее эту теорему уже доказали Люстерник и Шнирельман [9, с. 26].
Т е о р е м а 8.17 (Люстерник–Шнирельман). Пусть сфера Sn покрыта замкнутыми множествами F1, . . . , Fn+1. Тогда одно из них содержит пару диаметрально противоположных точек сферы.
Д о к а з а т е л ь с т в о. Обозначим через −Fi множество, симметричное Fi относительно центра сферы. Покажем, что если Fi ∩ (−Fi) =
при i = 1, . . . , n, то Fn+1 ∩ (−Fn+1) 6= .
Применив лемму Урысона (см. с. 67) к непересекающимся замкнутым множествам F1 и −F1, лежащим в Rn+1, можно построить непрерывную функцию ϕ1 : Sn → [0, 1], для которой ϕ1 (F1) = 0 и ϕ1 (−F1) = 1 (лемма Урысона даёт функцию f, для которой f(F1) = −1 и f(−F1) = 1; мы полагаем ϕ1 = (1 + f)/2). Аналогично построим функции ϕ2, . . . , ϕn. Рассмотрим отображение ϕ : Sn →Rn, заданное фор-
мулой ϕ(x) = (ϕ1 (x), . . . , ϕn (x)) |
. Согласно теореме Борсука–Улама су- |
|||
ществует точка |
x0 Sn, для |
которой |
ϕ(x0) = ϕ(−x0). Если |
x ±Fi, |
i = 1, . . . , n, то |
ϕi (x) − ϕi (−x) = ±1, |
поэтому ϕi (x) 6= ϕi (−x). |
Следо- |
|
