
топология / Tom Dieck T. Algebraic topology (EMS, 2008)
.pdf
48 Chapter 2. The Fundamental Group
We have the open covering of S1 C by X0 D S1 X f1g and X1 D S1 X f 1g with inclusions ik W X01 ! Xk and jk W Xk ! S1. The sets Xk are contractible, hence simply connected. Therefore there exists a single morphism .a; b/k W a ! b between two objects a; b of ….Xk /.
We have bijective maps f0 W 0; 1Œ ! X0 and f1 W 1=2; 1=2Œ ! X1 given by t 7! exp.2 it/. We define functors k W ….Xk / ! G by the identity on
1 |
|
D |
|
k |
|
|
|
|
k |
|
|
|
objects and by |
k .a; b/k |
|
.a; f |
1 |
.b/ |
f 1.a//. Moreover we have a functor |
||||||
W G ! ….S / which is the identity |
on objects and which sends the morphism .a; t/ |
|||||||||||
|
1 |
, |
|
7! |
a |
1 |
||||||
of G to the class of the path I |
! |
S |
|
s |
||||||||
|
|
|
a exp.2 its/ from |
|
to a exp.2 it/. |
|||||||
(The idea behind the definition of G is the fact that each path in S is homotopic to one of this normal form, see (2.7.9).) The following diagram is commutative.
|
….X0 |
/ |
|
…j0 |
|
|
|
|
…i0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
||
….X01/ |
|
|
|
|
|
|
|
|
|
|
|
G |
|
….S |
/ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…i1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…j1 |
|
|
|
|
|
….X1/ |
|
|
|
|
|||
(2.7.1) Proposition. The functor is an isomorphism.
Proof. We apply (2.6.1) to the pair . 0; 1/ and obtain a functor W ….S1/ ! G. The uniqueness property of a pushout solution shows D id. In order to showD id we note that the morphisms of G are generated by the images of 0 and 1. Given .a; t/ 2 G.a; b/, choose a decomposition t D t1 C C tm such that jtr j < 1=2 for each r. Set a0 D a and ar D a exp.2 i.t1 C C tr //. Then
.a; t/ D .am 1; tm/ ı ı .a1; t2/ ı .a0; t1/ in the groupoid G. Since jtr j < 1=2 there exists for each r a k.r/ 2 f0; 1g such that ar 1 exp.2 itr s/ 2 Xk.r/ for s 2 I . Then .ar 1; tr / D k.r/.ar 1; ar /k.r/. Thus G.a; b/ is generated by morphisms in the images of the k .
The unit circle S1 in the complex plane is the prototype of a loop. Typical elements in the fundamental group are obtained by running n times around the circle. Up to homotopy, there are no other possibilities. With (2.7.1) we have determined the fundamental group 1.S1; 1/, namely as the automorphism group in ….S1/ of the object 1. The automorphisms of the object 1 in G are the .1; n/; n 2 Z and.1; n/ is the loop t 7!exp.2 i nt/.
(2.7.2) |
Theorem. |
Let sn W |
I |
! |
S1 |
be the loop t |
exp.2 i nt/. The assignment |
||
|
1 |
|
|
|
|
7! |
|||
ı W Z ! 1.S |
|
; 1/, n 7!Œsn is an isomorphism. |
|
||||||
The circle S1 is a group with respect to multiplication of complex numbers. We show that the composition law in 1.S1; 1/ can also be defined using this multiplication.
2.7. The Fundamental Group of the Circle |
49 |
More generally, assume that X is a space with a continuous multiplication m W X X ! X; .x; y/ 7!m.x; y/ D xy
and neutral element up to homotopy e 2 X (the base point), i.e., the maps x 7!
m.e; x/ and x 7!m.x; e/ are both pointed homotopic to the identity. We call such an object a monoid in h-TOP. (We do not assume that m is associative or commuta-
tive.) We define a composition law on the pointed homotopy set ŒY; X 0, called the m-product, by Œf ; Œg 7!Œf m Œg D Œf g ; here f g W y 7!m.f .y/; g.y// is the ordinary pointwise multiplication. The constant map represents a two-sided unit for the m-product. In a similar manner we define by pointwise multiplication of loops the m-product on 1.X; e/. The set 1.X; e/ Š ŒS1; X 0 now carries two composition laws: the m-product and the -product of the fundamental group.
(2.7.3) Proposition. Let .X; m/ be a monoid in h-TOP. Then the -product and the m-product on 1.X; e/ coincide and the product is commutative.
Proof. Let k be the constant loop. Then for any two loops u and v the relations |
|
u v ' .u k/ .k v/ D .u k/ .k v// ' u v; |
|
u v ' u v ' .k u/ .v k/ D .k v/ .u k/ ' v u |
|
hold. In order to see the equalities, write down the definition of the maps. |
(2.7.4) Lemma. The map v W ŒS1; S1 0 ! ŒS1; S1 which forgets the base point is a bijection.
Proof. Given f W S1 |
! S1 we choose a path w W I ! S1 from 1 to f .1/ 1. |
|||||||
Then .x; t/ |
7!f |
|
|
1 |
|
1 |
|
|
|
|
|
.x/w.t/ is a homotopy from f to a pointed map, hence v is |
|||||
surjective. |
Let H W S |
|
I ! S |
|
be a homotopy between pointed maps; then |
|||
.x; t/ |
7! |
|
|
H.1; t/ 1 is a pointed homotopy between the same maps, i.e., |
||||
H.x; t/ |
|
|||||||
v is injective. |
|
|
|
|
|
|
||
If f; g W X ! S1 are continuous maps, then f g W x 7!f .x/g.x/ is again continuous. This product of functions is compatible with homotopies and induces the structure of an abelian group on ŒX; S1 .
(2.7.5) Theorem. From (2.7.2), (2.7.4) and (2.5.3) we obtain an isomorphism d ,
d W ŒS1; S1 Š ŒS1; S1 0 Š 1.S1; 1/ Š Z:
We call the integer d.fn/ D d.Œf / the degree of f W S1 ! S1. A standard map of |
|
degree n is n W z 7!z . A null homotopic map has degree zero. |
|
(2.7.6) Example. A polynomial function
g W C ! C; g.z/ D zn C a1zn 1 C C an has a root (n 1).
50 Chapter 2. The Fundamental Group
Proof. Suppose g.z/ 6D0 for jzj D 1. Then f W S1 ! S1, z 7!g.z/=jg.z/j is defined. Suppose g is non-zero for jzj 1. Then h.z; t/ D f .tz/ is a null homotopy of f . For t > 0 we have
k.z; t/ D zn C t.a1zn 1 C a2tzn 2 C C antn 1/ D tng.z=t/:
If g is non-zero for jzj 1, then H.z; t/ D k.z; t/=jk.z; t/j is a homotopy from
f to n. Thus if g has no root, then n is null homotopic; this contradicts (2.7.5).
The classical approach to 1.S1/ uses topological properties of the exponential function p W R ! S1, t 7!exp.2 it/. A lifting of w W Œa; b ! S1 along p is a map W W Œa; b ! R with pW D w; the value W .a/ is the initial condition of the
lifting. Liftings always exist and depend continuously on the path and the initial condition (see (2.7.8)).
(2.7.7) Proposition. Let f W S1 ! S1 be given. Let F W I ! R be a lifting of fp0 along p. Then F .1/ F .0/ is the degree of f .
Proof. Let g D f .1/ 1f . Then ı.d.f // D Œgp0 , by the definition of d in (2.7.5). There exists a 2 R such that f .1/ D exp.2 ia/ and F .0/ D a. Then ˆ D F a is a lifting of gp0 with initial condition 0. Hence F .1/ F .0/ D ˆ.1/ ˆ.0/ D ˆ.1/ D n 2 Z. The homotopy .x; t/ 7!.1 t/ˆ.x/ C txˆ.1/ is a homotopy of paths. Hence the loop gp0 is homotopic to sn. This shows ı.n/ D Œgp0 .
The next proposition will be proved in the chapter on covering spaces. It expresses the fact that p W R ! S1 is fibration.
(2.7.8) Proposition. Given a homotopy h W X I ! S1 and an initial condition a W X ! R such that pa.x/ D h.x; 0/. Then there exists a unique homotopy
H W X I ! R such that H.x; 0/ D a.x/ and pH D h.
(2.7.9) Example. Let w W Œ0; 1 ! S1 be a path with w.0/ D z D exp.2 ia/. Let W W Œ0; 1 ! R be a lifting of w with W .0/ D a. Suppose W .1/ D b. Then W is, by a linear homotopy, homotopic to t 7!a C t.b a/ and hence w homotopic to
the path in normal form t 7!z exp.2 i.b a/t/. |
Þ |
2.7.10 The winding number. Let x 2 C D R2. The map |
|
rx W C n fxg ! S1; z 7!.z x/=jz xj |
|
is an h-equivalence and therefore ŒS1; C n fxg ! ŒS1; S1 , Œf 7!Œrx f a bijection. The degree of rx f is the winding number of f with respect to x. We denote
it by W .f; x/. Maps f0; f1 W S1 ! C n fxg are homotopic if and only if they have the same winding number. If f W S1 ! C is given and w W I ! C a path with
|
|
2.7. The Fundamental Group of the Circle |
51 |
|
f .S |
1 |
/ \ w.I / D ;, then .x; t/ 7!rw.t/f is a homotopy. Therefore the |
|
1 |
|
|
|
winding |
|
numbers of f with respect to w.0/ and w.1/ are equal. The complement C n f .S / decomposes into open path components, and the winding number with respect to x
is constant as long as x stays within a component. |
|
|||||||
1 |
|
W |
I |
! C X f |
x |
g |
be a loop. Then there exists a unique continuous map |
|
Let u |
|
|
|
|||||
f W S |
! C X fxg such that f ı p0 D u. The winding number of f is then also |
|||||||
called the winding number of u, and we denote it by W .u; x/. |
Þ |
|||||||
The notion of the degree can be extended to other situations. Let h W S ! S1 be a homeomorphism and f W S ! S any map; the degree of hf h 1 is independent of the choice of a homeomorphism h and also called the degree d.f / of f .
Problems
1.Let p be a polynomial function on C which has no root on S1. Then the number of roots z with jzj < 1 (counted with multiplicities) is equal to the winding number W .pjS1; 0/. What is the winding number of the function 1=p with respect to 0?
2.(Properties of the degree.) d.f ı g/ D d.f /d.g/. A homeomorphism S1 ! S1 has
degree ˙1. If f W S1 ! S1 has degree d.f / ¤ 1, then there exists x 2 S1 such that f .x/ D x. The map z 7!zxhas degree 1.
Let u D exp.2 i=n/ be an n-th root of unity. Suppose h W S1 ! S1 satisfies h.uz/ D h.z/. Then d.h/ 0 mod n.
Let k; j 2 Z and assume that k is coprime to n. Let f W S1 ! S1 satisfy the functional equation f .uk z/ D uj f .z/. Then k d.f / j mod n. If, conversely, this congruence is satisfied with some integer d.f /, then there exists a map f of degree d.f / which satisfies the functional equation. In particular an odd map f , i.e., f . z/ D f .z/, has odd degree.
Suppose f . z/ ¤ f .z/ for all z; then the degree of f is odd. Suppose f .z/ ¤ g.z/
for |
all z; then d.f / |
D |
d.g/. Suppose d.g/ |
|
0 mod n for some n > 0; then there exists |
|||||||||||||||||||||||
|
1 |
! S |
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
h W S |
|
|
such that g D h |
|
. |
|
|
|
|
|
D C X 0 along the covering |
P W C |
! C |
|
, |
|||||||||||||
3. |
Let U W I ! C be a lifting of u W I ! C |
|
|
|
||||||||||||||||||||||||
z 7!exp.2 iz/. Then |
|
|
D |
U.1/ |
|
U.0/ |
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W .u; 0/ |
|
|
|
|
|
|
|
|
|
|
|
||||||
4. |
Let |
W |
Œ0; 1 |
! |
C |
1 be a |
continuously differentiable path with initial point 1 |
. Then |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d z |
|
|
|
|
|
|
|
|||||||||||
W Œ0; 1 ! C, t 7! |
|
jŒ0;t |
z is a continuously differentiable lifting of along P |
|||||||||||||||||||||||||
2 i |
||||||||||||||||||||||||||||
with initial point 0. |
|
|
|
R |
|
|
|
|
|
|
|
|
1 |
Ru |
dz |
|
|
|
||||||||||
5. |
If u W I ! C X fxg is a continuously differentiable loop, then W .u; x/ D |
|
|
|
. |
|
||||||||||||||||||||||
|
2 i |
z x |
|
|||||||||||||||||||||||||
6.Let A 2 GL2.R/. Then the winding number of lA W S1 7! R2 X 0, x 7!Ax with respect to the origin is the sign of the determinant det.A/.
7.Let v W ŒS1; X 0 ! ŒS1; X be the map which forgets about the base point (pointed homotopies versus free homotopies). Conjugate elements in the group ŒS1; X 0 have the same image under v. Hence v induces a well-defined map vxW ŒS1; X 0=. / ! ŒS1; X from the set of conjugacy classes. This map is injective, and surjective if X is path connected. Thus v is bijective if X is path connected and the fundamental group abelian.
52 Chapter 2. The Fundamental Group
2.8 Examples
The formal nature of the theorem of Seifert and van Kampen is simple, but the corresponding algebra can be complicated. The setup usually leads to groups presented by generators and relations. It may be difficult to understand a group presented in this manner. For an introduction to this type of group theory see [122]; also [171] and [39] are informative in this context. We report about some relevant algebra and describe a number of examples and different applications of the fundamental group.
2.8.1 Spheres. If a space X is covered by two open simply connected subsets with path connected intersection, then X is simply connected, since the pushout of two trivial groups is trivial. Coverings of this type exist for the spheres Sn for n 2. Hence these spheres are simply connected. Þ
2.8.2Removing a point. The inclusion Dn X 0 Dn induces for n 3 an
isomorphism of fundamental groups; actually both groups are zero, since Dn is contractible and Dn X 0 ' Sn 1.
Let M be a manifold of dimension n 3 and U M homeomorphic to Dn under a homeomorphism that sends x to 0. Then M is the pushout of M X fxg and U . Theorem (2.6.2) implies that M X fxg M induces an isomorphism of fundamental groups.
Often we view the space Sn as the one-point compactification Rn [ f1g of the
Euclidean space, see (2.3.2). Let K be a compact subset of Rn for n 3. Then the inclusion Rn X K Sn X K induces an isomorphism of fundamental groups. Þ
2.8.3Complements of spheres. Let S0m D SmCnC1 \ .RmC1 0/ and S1n D
SmCnC1 C1/. Then X D SmCnC1 X Sn is homeomorphic to Sm En.\ .0 Rn
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
A |
|
|
|
m |
|
n 1 |
m |
nE |
|
! X is .x; y/ 7!m |
1 n kyk |
x; y . The space |
|||||||||||
|
homeomorphism |
Sm |
|
|
n |
|
|
|
|
|
|
2 |
|
via .x; y; t/ |
|
||||||||
Y D S |
|
|
C C X .S0 [ S1 / is homeomorphic to S p S |
|
|
|
7! |
||||||||||||||||
|
|
0; 1Π|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y/. Therefore |
|
|
|
|
|
|
|
|
|
|
|
|||
.p1 |
|
|
|
|
|
t |
|
|
m n |
|
|
|
|
|
|
|
|
||||||
|
tx; p |
|
|
the complement X is h-equivalent to Sm and the com- |
|||||||||||||||||||
plement Y is h-equivalent to S |
|
3 S . |
1 |
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
fundamental group of S |
X .f0g S |
|
/ is isomorphic to Z. If we view |
||||||||||||||||
|
The 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
S |
|
D R |
|
[f1g, then we are considering the complement of the axis Z D f.0; 0; z/ j |
|||||||||||||||||||
z 2 Rg [ f1g. The generator of the fundamental group is |
a loop that runs once |
||||||||||||||||||||||
1 |
f0g. |
|
|||||||||||||||||||||
about the axis Z, represented by the standard sphere W D S |
|
|
|||||||||||||||||||||
It is impossible to span a 2-disk with boundary W in the complement of Z, because W represents a non-zero element in the fundamental group of the complement, see Figure 2.3. This is expressed by saying that W and Z are linked in S3.
Apply the stereographic projection (2.3.2) to S1 3 |
0 [ 0 S1 S3. The image |
||||||
yields W [ Z. The complement of W |
1[ Z |
1in R |
is therefore isomorphic to the |
||||
fundamental group |
Z Z |
of the torus S |
S . The reader should draw generators |
||||
|
3 |
|
|
||||
of 1.R |
|
X W [ Z/. |
|
|
|
Þ |
|
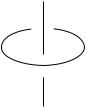
2.8. Examples |
53 |
1
W
Z
Figure 2.3. A standard circle in S3.
2.8.4 Presentation of groups by generators and relations. Let S be a set. A free group with basis S consists of a group F .S/ and a set map i W S ! F .S/ which has
the following universal property: For each set map ˛ W S ! G into a group G there exists a unique homomorphism A W F .S/ ! G such that A ı i D ˛. It turns out that i is injective. Let us consider i as an inclusion and set S 1 D fs 1 j s 2 Sg. A word in the alphabet X D S q S 1 is a sequence .x1; : : : ; xm/ of elements xi 2 X. The elements in F .S/ are the products x1 : : : xm corresponding to the words; the neutral element belongs to the empty word; a word .x; x 1/ also represents the neutral element.
R the image in F .S/. Let N.R/ be the normal sub- |
||
Let R be a set of words and x |
|
F .S/=N.R/ is the group presented |
R. The factor group G |
D |
|
group generated by x |
|
|
by the generators S and the relations R. We denote this group by h SjR i. It has the following universal property: Let ˛ W S ! H be a set map into a group H . Assume that for each .x1; : : : ; xm/ 2 R the relation ˛.x1/ : : : ˛.xm/ D 1 holds in H . Then there exists a unique homomorphism A W G ! H such that A.x/ D ˛.x/ for each x 2 S.
Each group can be presented in the form h S j R i – in many different ways. In practice one uses a less formal notation. Here are a few examples.
(i)The cyclic group of order n has the presentation h a j an i.
(ii)Let S D fx; yg. Consider the word .x; x; y 1; y 1; y 1/ and R consisting
|
|
|
|
2 |
|
|
3 |
D h |
j |
R |
i |
also in the form |
h |
x; y |
j |
x2y 3 |
i |
of this word. |
Then we can write G |
|
S |
|
|
|
|
||||||||||
or h x; y j x |
|
D y i. The universal property says in this case that homomor- |
|||||||||||||||
phisms G |
! |
H |
correspond bijectively to set maps ˛ W fx; yg ! H |
such that |
|||||||||||||
|
2 |
|
3 |
. |
|
|
|
||||||||||
˛.x/ |
|
D ˛.y/ |
|
|
|
|
|
|
|
|
|
|
|
||||
(iii) h a; b j ab D ba i is a presentation for the free abelian group with basis a, b.
Þ
2.8.5 Free product and pushout of groups. The sum (D coproduct) in the cate-
gory of groups is also called a free product. Let .Gj j j 2 J / be a family of groups. The free product of this family consists of a group k2J Gk together with a family

54 |
Chapter 2. The Fundamental Group |
|
|
of homomorphisms j W Gj ! |
k2J Gk which have the universal property of a |
||
|
(The notation G |
G2 is used for the free product |
|
sum in the category of groups. |
1 |
||
of two groups.) Each family has a sum. Let Gj D h Sj jRj i and assume that the Sj
are disjoint. Let S |
D q |
|
q |
S 1. Let |
|
j Sj . The Rj are then words in the alphabet S |
|
||||
R D |
S |
|
|
|
|
j Rj . We have homomorphisms j W h Sj jRj i ! h SjR i which are induced |
|||||
by Sj S. These homomorphisms are a sum in the category of groups. |
|
||||
Let G and H be groups and i1 W G ! G H , j1 W H ! G |
H be the canonical |
||||
maps which belong to the sum. Let J W P ! G, I W P ! H be homomorphisms from a further group P . Let N be the normal subgroup of G H generated by the elements fi1J.x/ j1I.x 1/ j x 2 P g. Let Q D .G H /=N and denote by i W G ! Q, j W H ! Q the composition of i1; j1 with the quotient map. Then
.i; j / is a pushout of .J; I / in the category of groups. In the case that I and J are inclusions (but sometimes also in the general case) one writes Q D G P H .
Let S be a set and Z D Zs a copy of the additive group Z for each s 2 S. Then |
||||||||||||||||||||
the groups F .S/ with basis S is also the free product s2S Z. |
|
|
|
|
|
|
|
|
Þ |
|||||||||||
2.8.6 Free products of fundamental groups. The free product 1.X0/ |
|
1.X1/ |
||||||||||||||||||
arises geometrically if X01 is simply connected. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Let X D S1 _S1 with X0 D Y _S1, X1 D S1 _Y , where Y D S1 Xf 1g;1 |
D |
|||||||||||||||||||
1. Then .Y; 1/ is pointed contractible; hence the inclusion of the summands S |
! |
|||||||||||||||||||
X0; X1 are pointed h-equivalences. |
One can apply (2.6.2) to the covering of X |
|||||||||||||||||||
by X |
0; X1. Since X0 \ X1 |
|
|
|
|
|
|
|
|
|
.X/ is the free |
|||||||||
|
is pointed contractible, we see that 1 1 |
1! |
|
1 |
_ |
|
1 |
|||||||||||||
product 1.X0/ 1.X1/. |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
S |
|
S |
|
|
||||
|
|
Hence the inclusions of the summands S |
/ |
|
|
|
|
. |
||||||||||||
yield a presentation of 1.S |
|
_ S |
|
/ as a free product |
1 |
.S / |
|
1 |
.S |
Š Z |
Z |
|||||||||
|
|
k |
|
|
|
|
|
|
||||||||||||
By induction one shows that 1 W1 |
S1 is the free group of rank k. |
|
|
|
|
|
Þ |
|||||||||||||
2.8.7 Plane without two points. The space R2 X f˙1g has as a deformation retract the union X of the circles about ˙1 with radius 1=2 and the segment from 1=2 to 1=2, see Figure 2.4. (The reader should try to get an intuitive understanding of a
1 ! 0 ! C1
u |
v |
Figure 2.4. Generators u; v of 1.R2 X ˙1/.
retraction. In order to give a formal proof, without writing down explicit formulas, it is advisable to wait for the method of cofibrations.) The fundamental group1.R2 X f˙1g; 0/ is the free group Z Z and generators are represented by two

2.8. Examples |
55 |
small circles about ˙1 (of radius 1=2, say) connected linearly to the base point. One can apply (2.6.2) to the covering of R2 X f˙1g by the punctured half-spaces f.x; y/ j x < 1=3; x 6D 1g and f.x; y/ j 1=3 < x; x 6D1g . Þ
In the example in 2.8.6 one cannot apply (2.6.2) directly to the covering of S1_S1 by the two summands, since the interiors do not cover the space. The general method in cases like this is to first “thicken” the subspaces up to h-equivalence. In the next theorem we add a hypothesis which allows for a thickening.
(2.8.8) Theorem. Let ..Xj ; xj / |
j j 2 J / be a family of pointed spaces with |
the property: The base point xj |
has an open neighbourhood Uj Xj which is |
pointed contractible to the base point. The inclusions of the summands induce homomorphisms ij W 1.Xj ; xj / ! 1 Wk2J Xk ; x . This family is a free product of the groups 1.Xj ; xj /.
Proof. Let J D f1; 2g. We apply (2.6.2) to the covering X1 _ U2; U1 _ X2 of
X1 _ X2. The argument is as for 2.8.4. For finite J we use induction on jJ j. Note that W Uj W Xj is an open, pointed contractible neighbourhood of the base point.
Let now J be arbitrary. A path w W I ! Xj has, by compactness of I , an im-
age in |
e2E Xe _ |
|
j |
2J XE Uj |
for a finite subset E |
|
J . This fact and the result |
||||||||||||||
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
show that the canonical map ˛ |
J W |
j 2J 1.Xj / ! 1 j 2J Xj |
is surjec- |
|||||||||||||||||
for E W |
|
|
W |
|
|
||||||||||||||||
tive. Each element x |
2 |
j 2J 1.Xj / |
is contained in some |
|
|
|
.X |
/ for a |
|||||||||||||
|
|
|
|
|
|
|
|
|
We2E |
|
1 |
e |
|
|
|
||||||
finite E. Suppose x is contained in the kernel of ˛ |
J |
. Then a loop w |
I |
! |
e2E |
X |
e |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
||||||
representing ˛ |
E |
x is null homotopic in |
j 2J Xj |
and, again by compactness, null |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|||
homotopic in some larger finite wedge. The result for a finite index set now yields |
|
W |
|
x D 0. |
|
2.8.9 Quotient groups. Let i W K ! G be a homomorphism of groups and denote by N C G the normal subgroup generated by the image of i. Then
K1
|
i |
|
|
|
|
p |
|
|
|
|
|
|||
G |
G=N |
|||
|
|
|
|
|
is a pushout in the category of groups, with p the quotient map.
This situation arises geometrically in (2.6.2) if one of the spaces X is simply connected. Þ
2.8.10 Attaching of a 2-cell. We start with a pushout diagram of spaces
'
S1 B
jJ
D2 ˆ X.

56 Chapter 2. The Fundamental Group
Then X is said to be obtained from B by attaching a 2-cell via the attaching map '. (This construction will be studied in detail in the chapter on cell complexes.) Then a suitable thickening shows that we can apply (2.6.2). Since D2 is contractible, we are in the situation of 2.8.9. Thus J induces an isomorphism 1.B/=h ' i Š 1.X/ where h ' i denotes the normal subgroup generated by Œ' 2 ŒS1; B 0 D 1.B/. Þ
2.8.11 Attaching of a cone. Given a map ' W A ! B from a path connected space A. The cone on A is the space A I=A 0. Let j W A ! CA, a 7!.a; 1/ denote the inclusion of A into the cone. The cone is contractible, a contracting homotopy is induced by ht .x; s/ D .x; s.1 t//. Form a pushout
'
AB
jJ
|
ˆ |
|
CA |
|
X. |
|
|
|
Since CA is contractible, J induces an isomorphism 1.B/=N Š 1.X/, where N is the normal subgroup generated by the image of ' . Þ
2.8.12 Realization of groups. We demonstrate that arbitrary groups can be realized as fundamental groups. Let
f W A D Wk2K S1 ! Wl2L S1 D B
be a pointed map. The inclusions of the summands yield a basis ak 2 1.A/ and bl 2 1.B/ for the free groups and f .ak / D rk is a word in the blt , t 2 Z. Let N l2L Z D G be the normal subgroup generated by the rk . Then G=N is the group presented by generators and relations h bl ; l 2 L j rk ; k 2 K i. Let CA be the cone on A and define X by a pushout diagram
|
|
|
f |
|||
|
|
|
|
|
|
|
A |
|
|
|
B |
||
|
\ |
|
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
X. |
|||
|
|
|
|
|
||
Then 2.8.11 shows 1.X/ Š G=N . Each group can be presented in the form G=N . Note that X is a 2-dimensional cell complex. Þ
2.8.13 Surfaces. The classification theory of compact connected surfaces presents a surface as a quotient space of a regular 2n-gon, see e.g., [44, p. 75], [167], [123]. The edges are identified in pairs by a homeomorphism. The surface F is obtained as a pushout of the type
|
1 |
|
' |
n |
|
1 |
||
|
|
|
|
|||||
S |
|
|
|
ˆ |
W1 |
S |
|
|
|
|
|
|
|
||||
|
|
|
||||||
|
|
|
||||||
D |
2 |
|
|
|
|
|
||
|
|
|
|
F . |
|
|||

2.8. Examples |
57 |
The attaching map ' is given in terms of the standard generators of 1 Wn1 S1 by the so-called surface-word.
In order to save space we refer to [44, p. 83–87] for the discussion of the fundamental group of surfaces in general. We mention at least some results. They will not be used in this text.
(2.8.14) Theorem. .1/ The fundamental group of a closed connected orientable surface Fg of genus g 1 has the presentation
1.Fg / D h a1; b1; : : : ; ag ; bg j a1b1a1 1b1 1 : : : ag bg ag 1bg 1 i:
.2/ The fundamental group of a closed connected non-orientable surface Ng of genus g has the presentation
1.Ng / D h a1; : : : ; ag j a12a22 : : : ag2 i:
.3/ The fundamental group of a compact connected surface with non-empty boundary is a free group. The number of generators is the finite number 1 .Fg /
where .Fg / is the so-called Euler characteristic. |
|
.4/ A simply connected surface is homeomorphic to R2 or S2. |
There are many different definitions of the genus. We mention a geometric property: The genus of a closed connected orientable surface is the maximal number g of disjointly embedded circles such that their complement is connected. The genus of a closed connected non-orientable surface is the maximal number g of disjointly embedded Möbius bands such that their complement is connected. The sphere has genus zero by the Jordan separation theorem. Þ
Problems
|
2 |
Let S1 |
R |
3 |
0 |
R |
be the |
|
2 |
|
|
|
|
|
D f |
.0; 0; t/ |
j |
|
t |
3 |
2 |
g |
1 |
|||||||||||||||
1. |
|
2 |
3 |
|
g. |
|
|
standard circle. Let D |
|
|
|
|
|
2 |
|
|
|
and |
||||||||||||||||||||
S |
|
.2/ |
D f 2 R j k k D |
2 |
2 |
|
1 |
.2/ |
[ |
D is a deformation retract of X |
D R X |
S . |
||||||||||||||||||||||||||
|
|
x |
|
|
|
|
x |
|
Then S |
|
|
|
|
|
|
|
||||||||||||||||||||||
The space X is h-equivalent to S |
|
_ S . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2. |
Consider the loop based at .0; 0/ in the plane as shown in Figure 2.5. Determine which |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Figure 2.5.
