6. Некоторые сведения о неравноточных измерениях.

Бывают случаи, когда одну и ту же физическую величину измеряют несколько раз, но не в одинаковых условиях, а с разной степенью точности. Например, определение длины волны спектральной линии по положению дифракционных максимумов разных порядков.

В этом случае в качестве оценки значения искомой величины принимается средне взвешенноеее значение, вычисляемое по формуле:

, 37

Здесь Р_i-вессоответствующей реализации, то есть некоторый коэффициент, зависящий от точностиi-того измерения. Подбор этих коэффициентов задача в общем случае не простая. Обычно их выбираютобратно пропорционально квадратам относительных ошибок,соответствующих реализаций. Дисперсиясредневзвешенногозначения рассчитывается по формуле:

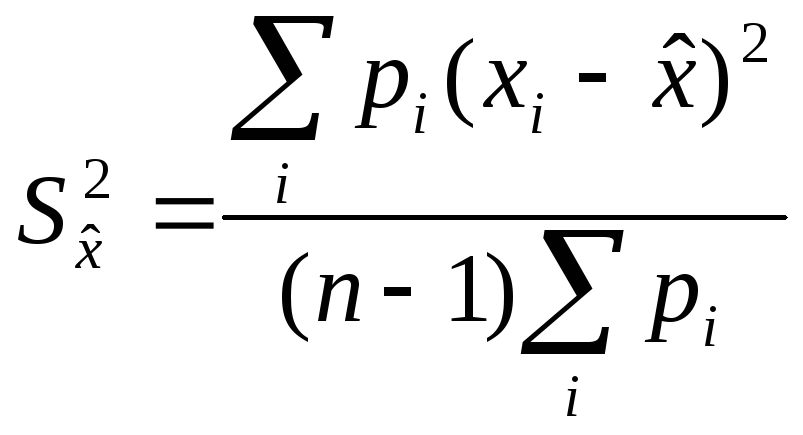38

Пример

Условие образования дифракционного максимума: d sin =  k, где k = 0,1,2,...– порядок спектра, d –постоянная решетки, а- угол дифракции. Следовательно, длину волны можно определить, измерив углыдля разныхk:

Поскольку постоянная решетки известна с большой степенью точности (ее погрешностью можно пренебречь), порядок спектра – целое число, то погрешность длины волны будет определяться погрешностью определения величины угла. Очевидно, что чем больше угол (больше порядок спектра), тем меньше будет относительная погрешность измерения угла (т.к. абсолютная погрешность прибора одинакова). Воспользовавшись формулой (17), можно получить:

Пусть в процессе измерений получены следующие значения углов:

При k=1φ₁ =1⁰15΄ctg φ₁= 45,8

k=2 φ₂ =2⁰30΄ ctg φ₂ = 22,9

k=3 φ₃ =3⁰42΄ ctg φ₃ = 15,5.

Таким образом, относительные ошибки в первом, втором и третьем порядках относятся как 3:2:1. Следовательно, веса следует выбирать: Р₁=1,Р₂=4,Р₃=9.

Получаем:

см=436,2 нм

Тогда среднее взвешенное значение будет равно:

=432,36 нм

Дисперсия среднего взвешенного:

S_λ =2,03нм Δλ= S_λ ∙t_p,n-1 = 2,03 ∙ 4,3= 8,7нм

Окончательный результат имеет вид λ= (432 ±9) нм

7.Учет погрешности приборов.

Если при измерении какой-либо величины при помощи физического прибора получают одно и то же значение при многократных измерениях, это не значит, что случайные погрешности определения этой величины равны нулю. Из этого факта будет следовать только то, что случайные погрешности при этих измерениях меньше систематических погрешностей, даваемых измерительными приборами, которые могут быть оцененыпо классу точности прибора. Приборная погрешность может быть указана или на самом приборе, или в его паспорте. В случаях, когда отсутствует паспорт прибора и не указан класс точности, приборную погрешность принято считать равной половине наименьшего деления шкалы прибора (половине цены деления шкалы)

При косвенных измерениях приборная (не исключенная систематическая) погрешность функции будет определяться (см. формул 20) через приборные погрешности аргументов по формуле:

39

Здесь Θ – приборная погрешность функции y, Θx_i - приборная погрешность величиныx_i

Пример.

Предположим, что измеряется сопротивление нагрузки путем измерения падения напряжения на ней и тока в цепи. Произведено пять измерений падения напряжения и пять измерений тока, которые дали совершенно одинаковые результаты. Измеренный ток I=5A, напряжениеВ

Искомое сопротивление равноОшибка! Ошибка связи.Ом.

Так как случайные погрешности не наблюдались, будем оценивать не исключенную систематическую погрешность, обусловленную предельной погрешностью измерительных приборов, используемых в эксперименте (классом точности).

Напряжения измеряется вольтметром, у которого предел измерения – 200 В, класс точности – 1,0. Относительная погрешность напряжения будет определена по формуле и численно равнатогда предельная абсолютная погрешность напряжения

Ток в цепи измеряется амперметром, его предел измерения –10 А, класс – 1,0. Относительная погрешность измерения тока 2%, а абсолютная величина предельной погрешности тока=0,1 А

Функция имеет вид, т.е. представляет собой частное двух аргументов, воспользовавшись формулой 23, получим выражение для вычисления погрешности сопротивления:

Тогда не исключенная систематическая погрешность сопротивления нагрузки