§2. Вычисление среднего арифметического

Вычисление среднего арифметического

(1)

Если выбрать значение близкое ктогда формулу (1) можно записать в виде

=(2)

Формула (2) оказывается более удобной чем (1) тогда, когда численное значение измеряемых величин имеют несколько значащих цифр. В этом случае приходится находить среднее арифметическое небольших разностей, а не самих больших чисел

§3. Другой вид формулы среднеквадратичной погрешности

По определению средняя квадратичная погрешность равна (см. формулы 12,13)

Числитель под корнем можно преобразовать:

Следовательно, среднеквадратичную погрешность можно записать в виде:

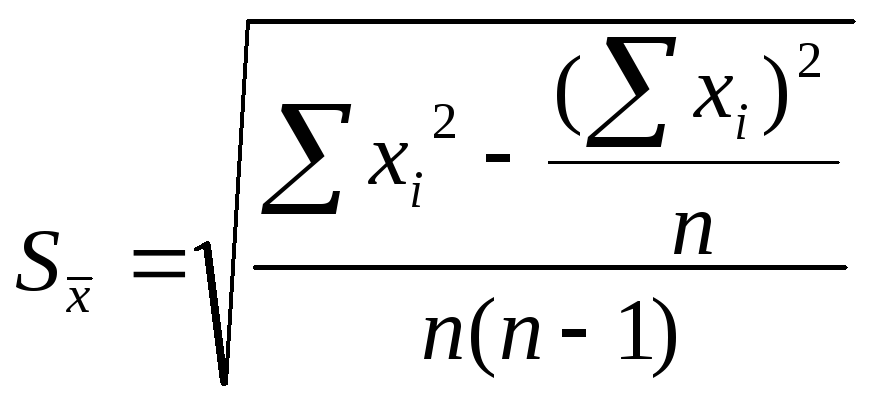
При использовании этой формулы алгоритм вычисления погрешности при прямых измерениях упрощается.

Хi	Xi2	= .
Х1	X12
Х2	X22
Х3	X32
…..
Хn	Xn2

Однако следует иметь в виду, что в эту формулу входит малая разность, поэтому расчет необходимо производить с большим числом значащих цифр. Если вы проводите вычисления с помощью компьютера, то это условие выполняется. В том случае, если расчеты выполняются «вручную», или с помощью не очень совершенного калькулятора, то надежнее использовать алгоритм, предложенный в главе 5 §1.

§ 4 Алгоритм вычисления погрешности при измерениях высокой точности § 5 Среднеквадратичная погрешность среднего арифметического

Пусть - результаты отдельных измерений, каждое из которых характеризуется одной и той же дисперсией

Найдем выражение для среднего арифметического:

Т.к. дисперсия суммы равна сумме дисперсий слагаемых, то дисперсия величины

При равноточных измерениях . Следовательно,

и .

Дисперсия среднего арифметического в раз меньше дисперсии отдельного измерения в серииизмерений. А среднеквадратичная погрешность среднеквадратичного враз меньше среднеквадратичного отдельного измерения. Из этого следует важный практический вывод: желая повысить точность измерений враз, нужно увеличить число измерений враз.

§ 6 Распределение Стьюдента

Распределение Стьюдента (впервые получено английским математиком В. Госсетом в 1908 г, который печатал свои работы под псевдонимом Стьюдент) выражается формулой

,

где - число измерений,t– коэффициент Стьюдента, Г() –гамма-функция, представляющая обобщенное понятие факториала ( для целых чисел Г(+1)=! Для полуцелых –Г=,Г=/2 и т.д.

Кривые функцииимеют такой же вид как и кривыераспределения Гаусса (см. рис.2).

При n→∞ (практически уже приn>20) распределение Стьюдента переходит в нормальное распределение Гаусса с единичной дисперсией (=1).

§ 7 Вычисление комбинации случайных и не исключенных систематических погрешностей по госТу

Вычисление суммарного интервала доверительной погрешности результата измерений в случае примерного равенства случайной и не исключенной систематической погрешности.

Если отношение не исключенной систематической погрешности измерения к случайной удовлетворяет неравенству:

0,8<<8

при доверительной вероятности P=0,95, то границы погрешности результата измерений (общие доверительные границы) вычисляют путем построения композиции распределения случайных и не исключенных систематических погрешностей, рассматриваемых как случайные величины, по формуле

,

где - коэффициент, зависящий от соотношения случайной и не исключенной систематической погрешностей, - оценка суммарного среднеквадратичного отклонения результата измерения.

Оценку суммарного среднеквадратичного отклонения результата измерения вычисляют по формуле

.

Коэффициент , зависящий оти, вычисляют по эмпирической формуле

,

где - доверительная граница средней квадратичной погрешности (), а- доверительная граница неисключенной систематической погрешности.

В развернутом виде выражение для имеет вид

Однако дробный множитель в этом выражении перед членом при изменении отношенияв пределах от 0,8 до 5,0 меняется лишь в пределах от 0,707 до 0,769,

Т.е. только на 8%, поэтому последняя формула может быть записана в виде

Здесь имеет ту же доверительную вероятность, что иидля которых необходимо выбирать одно и тоже значение доверительной вероятностиP.

?? § 8 Погрешность ф. многих переменных  вывод

?? § 9 МНК  вывод