3. Элементы теории вероятности и математической статистики.

Случайной называется величина, которая в результате опытов может принимать различные заранее неизвестные значения. Конкретное значение х_i , появляющееся в результате опыта, называется реализацией случайной величины.

Пусть i= 1,2,. . . ,Nномера опытов,Nих число, аx_iреализации, полученные при повторении опытов. Пустьх₀ – истинное значение случайной величины, нам неизвестное.

Обозначим Δx_i=x₀ ― x_i  абсолютную ошибкуi-го измерения, тогдаx_i= x₀ ― Δx_i. Просуммировав эти равенства по всемi, получим:

или

,

3

где среднее арифметическое всех реализаций. Можно показать, что второе слагаемое в этом выражении стремиться к 0, еслиNстремиться к бесконечности. То есть среднее арифметическое всех реализаций стремиться к истинному значению случайной величины при стремлении к бесконечности числа измерений. Можно сделать вывод, что увеличение числа измерений приводит к увеличению точности^.

Возможность тех или иных реализаций характеризуют вероятностьюих появления. При этом вероятность достоверного события принято считать равной 1, а невозможного – равной 0.

В том случае, когда величины x_i могут принимать непрерывный ряд значений, следует говорить не о вероятности конкретного значенияx_iа о вероятности попадания результата измерений в некоторый интервал Δx_i.Разобьем всю область значенийx на одинаковые интервалы шириной Δx каждый.

Найдем число реализаций ΔNi, попадающих в каждыйi- й интервал и относительную частоту их появления ΔNi/N Представим результаты графически. По оси абсцисс отложим значение величины x, а относительную частоту ΔNi/Nпредставим высотой полоски, построенной на интервале Δxiкак на основании. Полученный график носит название гистограммы и характеризует распределение данной серии наблюдений.

Рис.1

При большом числе измерений на гистограмме проявятся основные статистические закономерности:

1. полученные значения измеряемой величины симметрично распределяются относительно некоторого среднего значения ,

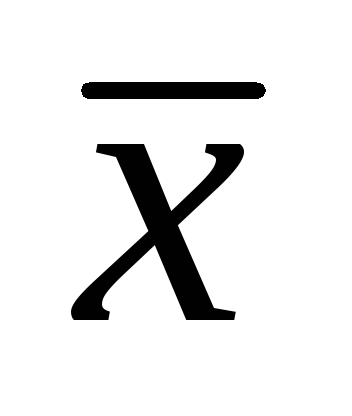2. большие отклонения от среднего будут встречаться реже, чем малые.

Если увеличивать число измерений и одновременно сужать ширину интервалов Δx, то в пределе при Δx→ 0 иN→ ∞ ломаная линия, огранивающая гистограмму сверху, будет стремиться к плавной колоколообразной кривой (рис2).

Рис.2

Такая кривая характеризует распределение результатов измерений при бесконечно большом числе наблюдений. Если при построении такой гистограммы по оси ординат откладывать относительную частоту появления реализации, отнесенную к единичному интервалу: ΔN_i/(N·Δx), то получающаяся в пределе кривая будет характеризовать распределениеплотности вероятностиполучения результатах_изм=х. Ордината этой кривой –плотность вероятности

4

Величина dP(x)=f(x)dx– вероятность того, что результат наблюдениях_измокажется в пределах от результатах до результатах+dx(рис. 2). Площадь под всей кривойf(x) имеет смысл появления хоть какого-нибудь результата наблюдений, то есть вероятности достоверного события, поэтому она равна единице. Это условие нормировки для непрерывной случайной величины.

5

Вероятность того, что измеренное значение будет лежать в интервале [x₁,x₂] определится выражением:

6

то есть, равна площади, ограниченной кривой f(x) в этом интервале.

Кривая распределения результатов характеризует гипотетическую совокупность бесконечного числа наблюдений данной величины. Максимум кривой соответствует наиболее вероятному значению х=. Форма кривой зависит от точности измерений. Если точность высокая – большие отклонения встречаются редко, – то кривая имеет вид острого пика. Большая ширина колокола означает наличие больших случайных отклонений, то есть меньшей точности.

Такая же кривая описывает и распределение ошибок. Достаточно перенести начало координат в точку х=и тогда по оси абсцисс вместохбудут отложены значения ошибок (отклонений от среднего)

Законы теории вероятностей построены как асимптотические при х0 иN. Математическая статистика приближенно использует эти законы при конечныххиN.

Теория вероятности утверждает, что случайные величины на практике наиболее часто подчиняются закону нормальногораспределения или закону распределенияГаусса. Его плотность, определяется выражением

f(x) = exp[]

7

Как видно из формулы (7) нормальная плотность распределения полностью определяется двумя параметрами теоретическим средним, и величиной², которую называютгенеральной дисперсиейраспределения. Значениезадает положение максимума^,² - его ширину. Величина дисперсии характеризует разброс результатов измерений (точность), чем меньше разброс, тем меньше будет², на графике это отразится как более узкий и высокий максимум.

Рис.3 Кривые нормального распределения Гаусса для трех значений параметра .

График этой функции изображен на рис 3

Параметр называется теоретическим средне квадратичным отклонением реализаций (или стандартным отклонением). Нетрудно убедиться, что в точкахx = ± σграфик функцииf(x) имеет точки перегиба.

Функция плотности распределения вероятности позволяет рассчитать теоретическое среднее значение реализаций измеряемой величины, его называют математическим ожиданиемх₀ случайной величины:

8

Величина генеральной дисперсиитакже может быть вычислена с помощью этой функции:

9

Вероятность Р того, что значение случайной величиных, получаемой при одном измерении, окажется внутри заданного интервала (х₁ <x <x₂) определится выражением:

,

10

Это выражение называют интегралом вероятности. Данное соотношение позволяет решить две задачи – можно задать необходимый интервал и найти соответствующую вероятность; а можно, наоборот, задав требуемую вероятность, найти интервал, в который попадает искомое значениех. На практике чаще пользуются второй возможностью.

Эту вероятность называют доверительной вероятностью, а границы интерваладоверительными границами.

Воспользовавшись интегралом (10) можно определить, что вероятности попасть при одном измерении в интервал:

x0 - σ< x < x0+σ	равна	0,683 (68,3%)
x0 - 2σ< x < x0+2σ	-	0,950 (95%)
x0 - 3σ< x < x0+3σ	-	0,997 (99,7%)

Видно, что вероятность того, что результат измерения отличается от среднего больше чем на 3σ, очень мала (0,3%), именно на основании этого факта такие результаты принято считатьпромахом– «правило трех сигм».

Иногда интеграл вероятности представляют в другом виде. Вводится новая переменная , которая определяется соотношением:

=(х -х₀)/σ, тогдаd=dх/σи интеграл вероятности (10) принимает вид:

11

Доверительные границы тогда будут определяться как Δх = σ. Величина определяется требуемой вероятностью.

Численные значения интегралов вероятности приводятся в специальных таблицах.

Из сказанного ранее следует, что с вероятностью 68,3% отдельная реализация будет отличаться от х₀(от математического ожидания) не больше, чем наσ; с вероятностью 95% - не больше чем на 2σ, соответственно и т. д.