4. Распределение Стьюдента.

На практике мы никогда не имеем дело с бесконечным числом измерений и не можем, следовательно, определить точно ни значение σ,ни значениех₀.

В качестве оценкизначения математического ожидания для выборки изnреализаций принято рассматривать их среднее арифметическое значение:

В качестве оценкидисперсии вводится величинавыборочной дисперсии и величинавыборочного среднеквадратичного отклонения, определяемые:

и

(12)

Можно показать, что при стремлении nк бесконечности→ σ².

Очевидно, что среднее арифметическое значение всех реализаций отличается от х₀ меньше чем отдельное значение. Другими словамидисперсия () и среднеквадратичное отклонение () среднего арифметического меньше чем дисперсия и среднеквадратичное отклонение отдельного измерения.В теории вероятности доказываются следующие соотношения:

и =σ2/n	(13)
и	(14)

Если мы имеем дело с конечным (и обычно не очень большим) числом измерений, то распределение уже не является Гауссовым. Качественно характер распределения подобен нормальному, но описывается другой функцией плотности распределения вероятности и носит название - распределение Стьюдента (псевдоним английского математика В. Госсета).

Распределение Стьюдента, в отличие от Гауссова, не определяется однозначно дисперсией и средним значением реализаций, а зависит еще от числа измерений n. В распределение Стьюдента входит параметрt, называемый коэффициентом Стьюдента, он зависит от двух величин – от числа измерений и от доверительной вероятности, поэтому указывается с двумя индексами: t_p,n. Таблица наиболее часто используемых коэффициентов Стьюдента приведена в приложении (§1). Коэффициент Стьюдента связывает среднеквадратичную ошибку среднего арифметического с величиной доверительного интервала.

(15)

Чем больше требуемая вероятность, тем больше коэффициент Стьюдента и, следовательно, больше доверительный интервал. С увеличением числа измерений значение коэффициента Стьюдента убывает.

Окончательный результат представляют в виде:

(16)

Как следует из сказанного, увеличение числа измерений необходимо для увеличения точности результатов. С ростом nсреднее арифметическое ближе к истинному значениюх₀ и доверительный интервал Δх при заданной вероятностиРбудет меньше.

Однако не следует забывать о существовании помимо случайных погрешностей еще и неисключенных систематических. Большое число измерений уменьшает только случайную ошибку, но, учитывая наличие систематической погрешности, проводить слишком большое число измерений нерационально.

5. Практические способы расчета случайных погрешностей

Математическая обработка результатов измерений является весьма трудоемким делом, зачастую отнимающим больше времени, чем сами измерения. Она требует внимания и аккуратности. Задача упрощается, если пользоваться соответствующими алгоритмами, которые представляют собой план рациональной последовательности действий при нахождении результата и его погрешности.

§ 1. Обработка прямых измерений (алгоритм прямых измерений).

Пусть искомая величина x измеренаn раз, для нахождения и, рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.

Таблица 1

№	xi	xi 	(xi -)2
1	x1	x1 	(x1 -)2
2	x2	x2 	(x2 -)2
3	x3	x3 	(x3 -)2
	…..	……	……….
n	xn	xn 	(xn -)2

1. Найти сумму всех x.

2. Найти =

3. Заполнить третий и четвертый столбцы таблицы.

4. Сосчитать сумму в четвертом столбце

5. Рассчитать среднеквадратичную погрешность среднего арифметического, используя полученную в четвертом столбце сумму.

6. Найти в «таблице коэффициентов Стьюдента» t_n-1,P для данного числа измерений и выбранной вероятности.

7. Определить

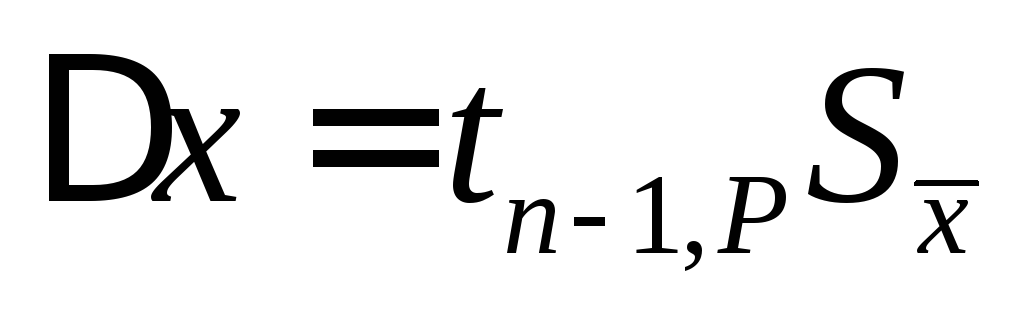
8. Записать окончательный результат .

Пример. Пять раз измерен диаметр проволоки с помощью микрометра. Получены следующие результаты (столбец 2).

Таблица 2

№	di, мм	di,мм	(di)2,
1	3,90	0,01	1104
2	3,85	0,06	36104
3	3,88	0,03	9104
4	3,97	0,06	36104
5	3,95	0,04	16104
	19,55		98104

=19,55 / 5 =3,910 мм

мм

Для доверительной вероятности Р=0,95 и числа измерений n=5, коэффициент Стьюдента=3,2, тогда

=3,20,022= 0,070 мм.

Окончательный результат: = (3,910,07_P=0,95 ) мм.

Относительная погрешность _d = (0,07 / 3,91)100% = 1,8%.

Возможны и другие алгоритмы и способы расчета, смотри приложение §§3,4.