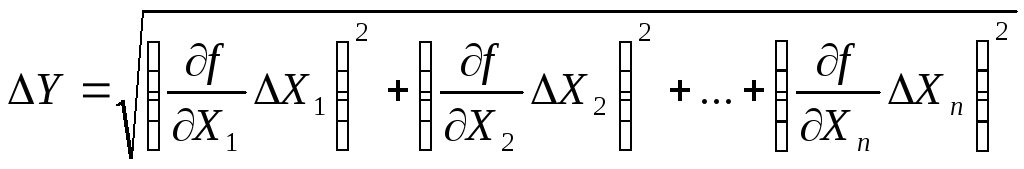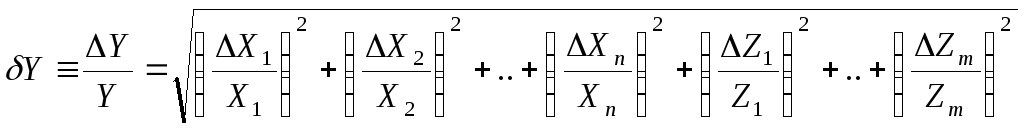 3 Обработка косвенных измерений. Функция многих переменных. (Формулы переноса ошибок)

В общем случае искомая физическая величина может быть функцией не одной, а нескольких измеряемых величин, то есть: Y=f(X₁,X₂,…X_n)^Каждая из величинX₁,X₂,…X_n определяется с соответствующей погрешностью X₁,X₂,…X_n. В этом случае средняя квадратичная погрешность этой функции будет равна корню квадратному из суммы квадратов частных производных функции по всем независимым переменным, домноженным на среднеквадратичную погрешность соответствующей величины (вывод этой формулы можно посмотреть в приложении п.6):

(3)

В данной формуле каждая скобка под корнем представляет собой вклад погрешности соответствующей величины в погрешность функции. Если погрешности различных измеряемых величин определены с одной и той же доверительной вероятностью, то формулу можно переписать в следующем виде:

(4)

Приведенные формулы справедливы для любых функциональных зависимостей, однако, они довольно громоздки, производить по ним расчеты бывает достаточно сложно, они требуют больших затрат времени. В некоторых случаях бывает удобнее использовать выражения, преобразованные для частных случаев функциональной зависимости. Рассмотрим несколько таких частных случаев.

Погрешность алгебраической суммы

Пусть функция имеет вид:

Y= , тогда среднеквадратичная погрешность такой функции будет определяться:

(5)

а выборочная дисперсия:

(6)

То есть выборочная дисперсия алгебраической суммы равна сумме выборочных дисперсий отдельных независимых переменных. Обратите внимание, на то, что в выражение для выборочной дисперсии функциивсе слагаемые входятсознаком «+»,независимо от того с каким знаком соответствующая величина входила в алгебраическую сумму.

Погрешность произведения.

Пусть функция имеет вид:

или

В этих случаях, воспользовавшись формулой (2) и, учитывая то, что логарифм произведения равен сумме логарифмов, получаем выражение для относительной погрешности функции:

(7)

То есть относительная погрешность произведения (и частного) равна корню квадратному из суммы квадратов относительных погрешностей всех сомножителей. Также как и в случае суммы, обратите внимание, на то, что все слагаемые под корнемберутся со знаком «+», независимо от того в числитель или знаменатель выражения функции они входили.

Производить расчет по этой формуле обычно гораздо проще, чем по формуле (3), а доверительный интервал искомой величины легко найти:.

Погрешности некоторых элементарных функций.

1. , где С=const;

2. ;

3. ;

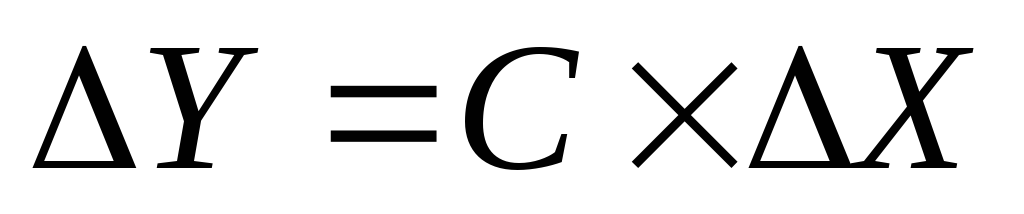
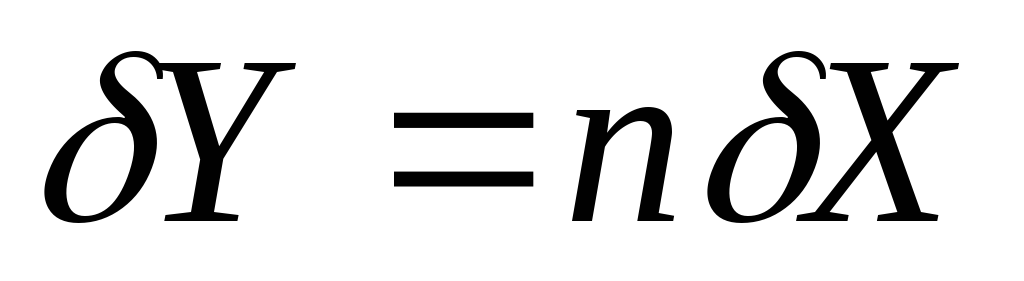
 4. Два способа оценки погрешности при косвенных измерениях.

В случае косвенных измерений физических величин возможны два способа вычисления окончательного результата и погрешности.

Первый способ.

Для каждой измеряемой физической величины проводят серию измерений. Эти измерения (прямые) обрабатывают и находят средние значения и соответствующие им доверительные интервалыс одной и той же доверительной вероятностью. Затем по выражению функциональной зависимостиY=f(X₁,X₂,…X_n) находят среднее значение искомой физической величины, используя найденные средние значения всех измеренных величин. Затем по формулам переноса ошибок (формула 4 или ее частные случаи) рассчитывают доверительный интервал величиныY.

Пример

Задача определить ускорение свободного падения с помощью математического маятника.

Формула для расчета , гдеlдлина маятника,Tпериод его колебаний.

Измерили 5 раз длину маятника и 5 раз его период. Получили следующие значения, которые обработали, как прямые измерения:

	l(м)	(м)		0,9644 =0,00051 0,000513,2=0,0016
1	0,965	0,0006	3,6 10-7
2	0,966	0,0016	25,610-7
3	0,964	-0,0004	1,610-7
4	0,963	-0,0014	19,610-7
5	0,964	-0,0004	1,610-7
	4,822		5210-7

	Т(сек)	Т	(Т)2	1,9698 =0,000583 0,0005833,2 =0,0018660,0019
1	1,970	0,0002	0,0410-6
2	1,969	-0,0008	0,6410-6
3	1,971	0,0012	1,4410-6
4	1,968	-0,0018	3,2410-6
5	1,971	0,0012	1,4410-6
	9,849		6,810-6

Получили: 0,9644и1,9698.

Затем рассчитывают ==9,812342

и, в соответствии с формулой (7) рассчитывают относительную погрешность g:

==0,0025400,0025.

Тогда g= gg =9,812342 0,0025=0,0249 0,025, и окончательный результат, соответственно: (9,8120,025) м/с² при Р=0,95

Второй способ.

В случаях, когда по условиям опыта измерения делаются в не воспроизводимых условиях, значения функции, Y=f(X₁,X₂,…X_n) вычисляют для каждой отдельной серии измерений{X_i}, а затем полученный ряд значенийY_i , обрабатывают по алгоритму прямых измерений.

Пример

Пусть поставлена та же задача определитьg, но при этом имеется несколько (пять) заведомо различных маятников. В этом случае рационально поступить следующим образом. Для каждого маятника измерить его длину и период колебаний. По этим значениям рассчитать величинуg (для каждого маятника независимо). Полученные значенияg обработать, как прямые измерения.

№ маятника	L(м)	Т(сек)	g (м/с2)
1	0,965	1,970	9,816453	0,00355	0,12603210-4
2	1,222	2,222	9,771086	-0,041817	17,4866910-4
3	1,568	2,510	9,825584	0,01268	1,6079510-4
4	0,559	1,498	9,834401	0,0215	4,6216710-4
5	0,752	1,739	9,816991	0,00409	0,16715210-4
			49,06452		24,009510-4