Элементы теории вероятности и математической статистики.

Эту вероятность называют доверительной вероятностью, а соответствующий интервалдоверительным интервалом.

Распределение Стъюдента. Способы расчета случайных погрешностей.

Математическая обработка результатов измерений является весьма трудоемким делом, зачастую отнимающим больше времени, чем сами измерения. Она требует внимания и аккуратности. Задача упрощается, если пользоваться соответствующими алгоритмами, которые представляют собой план рациональной последовательности действий при нахождении результата и его погрешности.

 1. Обработка прямых измерений (алгоритм прямых измерений).

Пусть искомая величина Х измеренаn раз, для нахождения и, рекомендуется записать данные в следующую таблицу и производить расчеты в указанном порядке.

Таблица 1

№	Хi	Хi 	(Хi -)2
1	Х1	Х1 	(Х1 -)2
2	Х2	Х2 	(Х2 -)2
3	Х3	Х3 	(Х3 -)2
	…..	……	……….
n	Хn	Хn 	(Хn -)2

1. Найти сумму всех Х.

2. Найти =

3. Заполнить третий и четвертый столбцы таблицы.

4. Сосчитать сумму в четвертом столбце

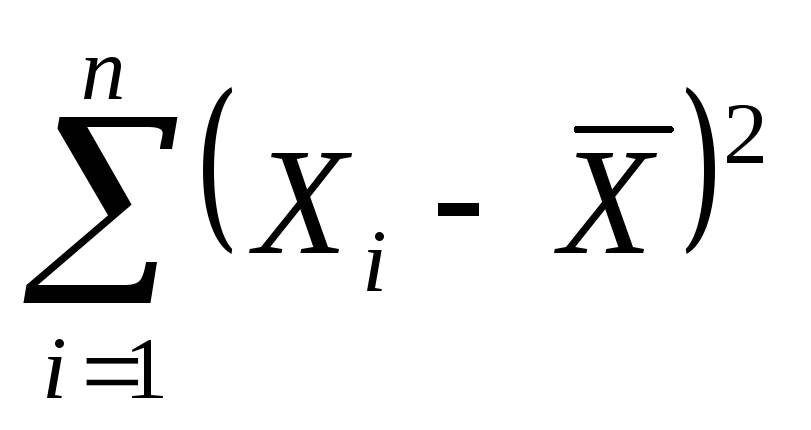
5. Рассчитать среднеквадратичную погрешность среднего арифметического, используя полученную сумму

6. Определить

7. Записать окончательный результат .

Пример. Пять раз измерен диаметр проволоки с помощью микрометра. Получены следующие результаты (столбец 2).

№	di, мм	di,мм	(di)2,
1	3,90	0,01	1104
2	3,85	0,06	36104
3	3,88	0,03	9104
4	3,97	0,06	36104
5	3,95	0,04	16104
	19,55		98104

=19,55 / 5 =3,910 мм

мм

Для доверительной вероятности Р=0,95 и и числа измерений n=5, коэффициент Стьюдента=3,2, тогда

=3,20,022= 0,070 мм

Окончательный результат: = (3,910,07_P=0,95 ) мм

Относительная погрешность _d = (0,07 / 3,91)100% = 1,8%

Возможны и другие алгоритмы и способы расчета, смотри приложениепункт7.

 2. Обработка косвенных измерений. Функция одной переменной. (Формулы переноса ошибок).

Пусть искомая физическая величина Yявляется функцией измеряемой величиныX.

Y =f(X)

Так как величина X не может быть определена абсолютно точно, то и рассчитанное значениеY будет содержать погрешность. Значение искомой функции следует находить, как функцию среднего арифметического значения измеренной величины, то есть в формулу для ее определения подставить вычисленное среднее значение

Как определить погрешность функции, если известна погрешность аргумента?

Для этого пользуются известным соотношением между дифференциалом функции df(X)и бесконечно малым приращением аргументаdX:

Полагая XdX, аYdY , получаем выражение для погрешности функции:

(1)

где X =t_p,n-1 S_X  производная функцииприX=.

Иногда оказывается удобнее (проще) вычислить сначала относительную погрешность, а уже зная ее, определить доверительный интервал. Учитывая то, что: легко видеть, что относительную погрешность функции можно вычислить, воспользовавшись следующей формулой:

(2)