1.2.1 Определение ширина дна канала
Отсюда вычислим ширину дна канала b:
Для того, чтобы определить, размывается канал или нет, воспользуемся расходной характеристикой K
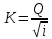
[1, Рис. 8.13, стр.99]
-
[1, Рис. 8.13, стр.99]
-
скорость
потока жидкости
[1,
табл. 11-3, стр.197]
,
следовательно, канал не размывается
Ширина дна канала b=0,605h = 0.605 * 3,25 = 1,97м [1, Рис. 8.13, стр.99]
1.2.2 Определим критическую глубину
,
где α=1.1 - критическая глубина прямоугольного
сечения
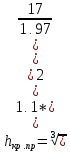
Полученное
начение критической глубины в канале
прямоугольного сечения подтверждается:
при
-
[1, табл. 9-1, стр.106]
Для нахождения критической глубины трапецеидального сечения применим формулу Агроскина:
[1, ф. Агроскина, стр. 108]
1.2.3 определение максимальной глубины
1.2.4 определение строительной глубины
-
запас
[2, стр.299]
1.2.5 принимаю ширину дамбы
-
ширина дамбы
1.2.6 принимаю ширину бермы
-
ширина бермы
1.2 Расчет критической глубины. Длины кривой свободной поверхности
- критическую глубину hкр и энергетическое состояние потока в канале (спокойный, бурный)
- Для гидравлически наивыгоднейшего профиля канала рассчитать одним из известных в гидравлике методов длину распространения кривой свободной поверхности потока в канале. За верхнюю по течению граничную глубину кривой hгр1 принять глубину (1,02÷1,03)hо или (0,98÷0,97)h0 в зависимости от вида кривой (кривая подпора или спада). За нижнюю граничную глубину принять заданную в таблице 2 величину hгр2.
Дано:
,
расход
;
- ширина канала по дну;
- уровень воды в канале;
- коэф. Откоса;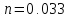
относительная шероховатость ;
- верхняя граничная глубина;
- нижняя граничная глубина;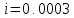
- уклон дна;
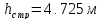- строительная глубина
1.2.1
Произведем расчет формы свободной
поверхности
- эту величину можно получить с помощью
формулы Бахметьева Б.А.:
,
-
параметр кинетичности,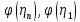
- функции Бахметьева
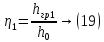
где
C-коэф.
Шези, i-уклон,
B-ширина
зеркала воды, g-ускорение св. падения,
-cмоченный
периметр.
1.2.1.1 Вычислим необходимые величины при :
Площадь
поперечного сечения:
;
Смоченный
периметр:
;
Гидравлический
радиус :
;
Коэффициент
Шези
;
Ширина зеркала воды:
Где
Получим параметр кинетичности:
1.2.1.2 Вычислим необходимые величины при :
Площадь
поперечного сечения
Смоченный
периметр
Гидравлический
радиус
Коэф.
Шези
Ширина
зеркала воды
,
где
,
,
,
Получим параметр кинетичности:
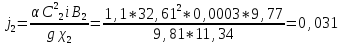
найдем среднее значение параметра кинетичности:
1.2.1.3 Непосредственно расчет
1) найдем значение функций Бахметьева, воспользовавшись справочником:
[1, табл. 9-3, стр 110]
[1,
табл 9-15, стр 110]
2) Найдем отношение глубины воды к ширине канала по дну:
3) По найденному отношению определяем значения x, обратившись к справочнику Кисилева.
[1,
9-15, стр. 110]
4) Получив значение х, по имеющимся таблицам определяем значения функции Бахметьева, при надобности аппроксимируем.
[1,
табл 9-15, стр 110]
[1,
табл 9-15, стр 110]
[1,
табл 9-15, стр 110]
значение, полученное для x=4.4,
вычисленные ранее значения подставляем в формулу Бахметьева:
