
Биостатистика / Biostat_2011_06
.pdf
Проблема множественных сравнений
....если на одном и том же наборе данных выполняется проверка большого числа гипотез, то при проверке каждой статистической гипотезы закладывается возможность ошибки первого рода (т.е. отклонение верной нулевой гипотезы). Чем больше гипотез мы проверяем на одних и тех же данных, тем больше будет вероятность допустить как минимум одну такую ошибку. Этот явление называют
эффектом множественных сравнений (multiple testing)...
Три выборки А, В и С.
Сравнение по критерию Стьюдента, Уровень значимости – a<0,05
При сравнении групп A и В риск ошибиться с вероятностью 5%. Точно такая же вероятность ошибки будет иметь место и при сравнении В с С и А с С. Соответственно, вероятность ошибиться хотя бы в одном из этих трех сравнений
составит:
p¢ = 1 - ( 1 -a )m = 1 - ( 1 - 0 ,05 )3 = 0 ,143
Это гораздо выше 0,05. Очевидно, что дальнейшее увеличение числа проверяемых гипотез будет неизбежно сопровождаться возрастанием в каждом отдельном тесте ошибки 2 рода (снижение мощности критерия).
http://r-analytics.blogspot.ru/2013/10/blog-post.html#.UyPQomeIq9I

FWER (familywise error rate) –
групповая вероятность ошибки первого рода — одна из мер, обобщающих ошибку первого рода, рассматриваемую при проверке статистических гипотез, на многомерный случай задачи множественной проверки гипотез. Величина определена как вероятность совершить хотя бы одну ошибку первого рода.
Спомощью критерия Стьюдента проверяем истинность m нулевых гипотез, которые
можно обозначить как H1,H2,H3,…,Hm .
|
Число |
Число |
Всего |
|
принятых |
отвергнутых |
|
|
|
||
|
гипотез |
гипотез |
|
Число верных |
U |
V |
m0 |
гипотез |
|||
Число неверных |
T |
S |
m−m0 |
гипотез |
|||
Всего |
W |
R |
M |
|
m0 - число верных нулевых гипотез ;
m−m0 - число истинных альтернативных гипотез ;
U - число безошибочно принятых гипотез ;
V - число ошибочно отвергнутых гипотез ;
T - число ошибочно принятых гипотез ;
S - число безошибочно отвергнутых гипотез;
W - общее число принятых гипотез;
R - общее число отвергнутых гипотез
В ходе выполнения анализа часть правильных Нi ошибочно отвергнута (V ), тогда как остальные U гипотез классифицированы правильно.
Аналогично, из альтернативных гипотез, S гипотез безошибочно отвергнуты, а T гипотез - ошибочно приняты.
Задача - минимизировать число ложных отклонений V и ложных принятий T .
Традиционно пытаются минимизировать величину V . Если V≥1 , мы совершаем как минимум одну ошибку первого рода. Вероятность допущения такой ошибки
(FWER) = P(V≥1) .
Соответственно, контролирование групповой вероятность ошибки на определенном уровне значимости α , подразумевает выполнение неравенства FWER≤α.
Методы множественной проверки гипотез как раз и позволяют обеспечивать этот контроль.
http://www.machinelearning.ru/wiki/index.php?title=FWER#cite_note-hochberg-0
Решение проблемы
На уровне организации эксперимента
Снижение числа гипотез Факторный анализ Структурное моделирование Изменение дизайна эксперимента
В режиме экстренного выхода из ситуации
Метод Бонферрони Метод Холма Метод Хохберга Метод Шидака minP
Перестановочные методы (permutation tests) Метод Хоммеля
Последовательная проверка
Контроль FWER для иерархических семейств гипотез

Как избежать фальшивых открытий? (Метод Бонферрони)
При проведении m независимых статистических тестов на уровне значимости a , вероятность хотя бы одного фальшивого результата должна быть
1-(1-a)m < 0.05
1 |
|
0 ,05 |
Carlo Emilio |
|
|
|
|||
a = 1 - ( 1 - 0 ,05 ) |
m |
» |
(1892 – 1960) |
|
|
|
|
|
Bonferroni |
|
|
|
m |
|
Правило Карло Бонферрони (1935):
При проведение m независимых статистических тестов
значимы только те результаты, для которых
p = 0 ,05 m
http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/

http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/
Bonferroni method creates more problems than it solves
Александр
Владимирович
РУБАНОВИЧ
qИнтерпретация данных зависит от числа тестов. Это противно нашей интуиции. Данные не могут терять
значимость от того, что их кто-то подтвердил!
qПри большом количестве тестов гипотеза
отом, что все наблюдаемые различия неслучайны, никому не нужна
qПри коррекции Бонферрони вероятность упустить существенные различия столь велика, что
…лучше просто перечислить какие тесты дали значимые результаты и, главное, почему
...Поправки Bonferroni, в лучшем случае, не нужны и, в худшем случае, вредны для формирования статистический выводов...
(Thomas Perneger, 1998):
Из разговоров на форуме molbiol.ru:
q…мы не будем гробить свои результаты из-за
какого-то там Бонферрони
q…спрашивать диссертанта о Бонферрони – это дурной тон
q…«бонферронофобия» набирает обороты
q…разработчики программ не желают вводить кнопочку «Bonferroni»
q…хуже Бонферрони ничего нет, не считая отсутствия всякой коррекции
http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/
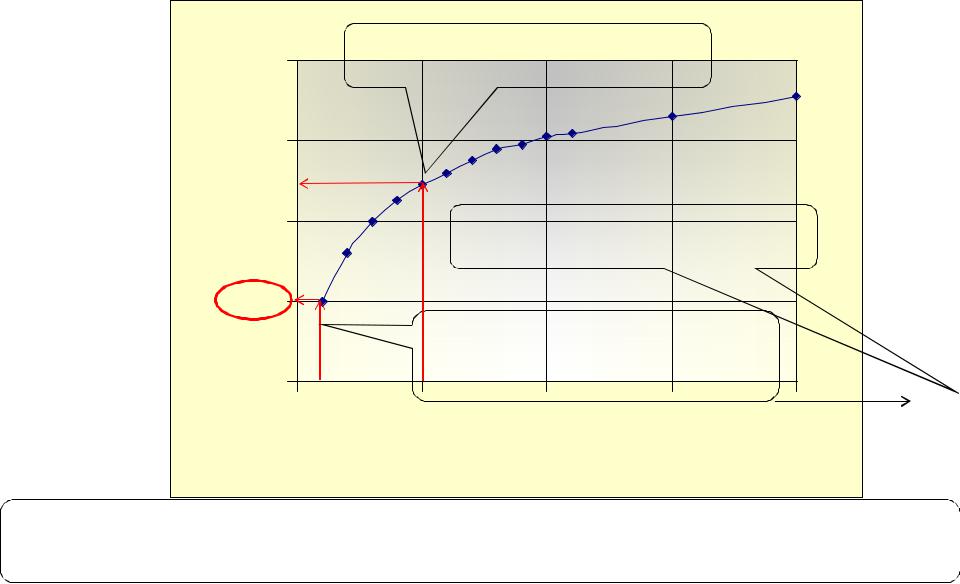
Зависимость ошибки II рода (мощность критерия) от |
|||||
числа тестов при использовании поправки Бонферрони |
|||||
|
0,8 |
При 5 сравнениях упускаем |
|
||
|
50% открытий |
|
|
||
II рода |
0,6 |
|
|
|
|
0,4 |
|
|
|
|
|
Ошибка |
|
При m=100 ошибка равна 0.88 |
|||
|
|
||||
0,2 |
В отдельном тесте |
|
|
||
|
|
|
|||
|
0 |
вероятность упустить |
|
||
|
открытие равна 0.2 |
|
|
||
|
0 1 |
5 |
10 |
15 |
20 |
|
|
|
Число тестов |
|
|
При 100 сравнениях ради того, чтобы гарантировать отсутствие хотя |
|||||
бы одного ложного результата, мы упускаем 88% открытий! |
|||||
http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/
A Simple Sequetially Rejective Multiple Test Procedures, Scand J Statist, 6, p 65-70 (1978)
Метод Холма-Бонферрони (также Метод Холма (1979), Поправка Холма-Бонферрони)
FDR-контроль
False Discovery Rate control: Benjamini, Hochberg (1995) |
Sture Holm |
|
Суть подхода Вероятность фальшивого открытия < Уровня значимости
Ошибка 1 рода < 0.05
Средняя доля фальшивых открытий < Выбранный уровень
æ |
Число _ неправильно _ отвергнутых _ нулевых _ гипотез |
ö |
|
|
ç |
÷ |
|
||
Eç |
|
÷ |
< 0 ,05 |
|
Число _ отвергнутых _ нулевых _ гипотез |
||||
è |
ø |
|
FDR является равномерно более мощным, чем поправка Бонферрони и решает проблему падения мощности при росте числа гипотез.
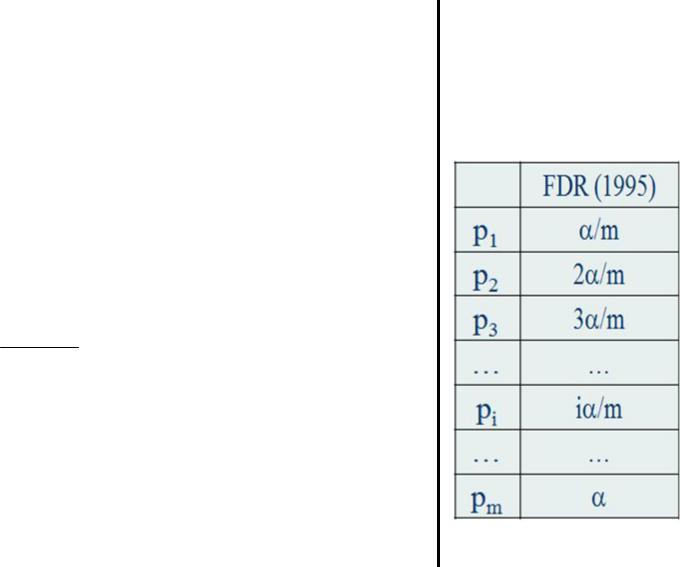
Алгоритм контроля FDR (Холм, 1978)
(Benjamini, Hochberg, 1995)
Метод предполагает всего лишь три шага:
1.Выстраивание всех полученных для m
нулевых гипотез Hо(i) уровней значимости p(i) в порядке возрастания;
2.Последовательная проверка неравенства
p( i ) <= i ×a
m
3. Отвержение всех нулевых гипотез
Hо(i)….Hо(k) , где k — первое i, для которого выполняется указанное неравенство.
m – число сравнений,
a =0.05
http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/
Пример: множественные сравнения по 10 тестам
Тест |
pi |
Коррекция |
Коррекция по |
Bonferroni |
FDR |
||
1 |
0,001 |
0,005 |
0,005 |
2 |
0,0055 |
0,005 |
0,010 |
3 |
0,01 |
0,005 |
0,015 |
4 |
0,015 |
0,005 |
0,020 |
5 |
0,02 |
0,005 |
0,025 |
6 |
0,04 |
0,005 |
0,030 |
7 |
0,3 |
0,005 |
0,035 |
8 |
0,5 |
0,005 |
0,040 |
9 |
0,6 |
0,005 |
0,045 |
10 |
0,8 |
0,005 |
0,050 |
http://vigg.ru/institute/subdivisions/otdel-geneticheskoi-bezopasnosti/laboratorija-ehkologicheskoi-genetiki/rubanovich-presentations/
