ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Статистические методы можно разделить на :
1.Методы оценивания параметров.
Важны свойства состоятельности, несмещенности, эффективности оценок.
2. Методы сравнения распределений или оцениваемых параметров, оценка статистической значимости различий.
Важны: корректность формулировки нулевой и альтернативной гипотез, выбор критерия и уровня
значимости и мощность критерия.
3. Методы классификации, кластеризации, распознования образов, ординации.
Обычные задачи статистического оценивания, с которыми студенты бакалавриата биологического факультета могут столкнуться в процессе работы над ВКР
Подготовка (оптимизация) данных для статистического анализа
Расчет основных статистик вариационного ряда
Нахождение доверительного интервала
Сравнение двух выборок
Сравнение нескольких (>2) выборок
Анализ статистических комплексов
Определение тесноты связи между переменными
Анализ характера связи между переменными
He uses statistics as a drunken man uses lamp-posts - for support rather than illumination.
Andrew Lan
ОПТИМИЗАЦИЯ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ ДЛЯ ЦЕЛЕЙ СТАТИСТИЧЕСКОГО АНАЛИЗА.
Задачу решают в ходе:
АНАЛИЗА ХАРАКТЕРА И ПРИЧИН ВАРЬИРОВАНИЯ ВАРИАНТ
сиспользованием процедур:
-ПРОВЕРКИ СОМНИТЕЛЬНЫХ ВАРИАНТ и
-ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА ИЛИ РЕЖИМА ПРОБООТБОРА.
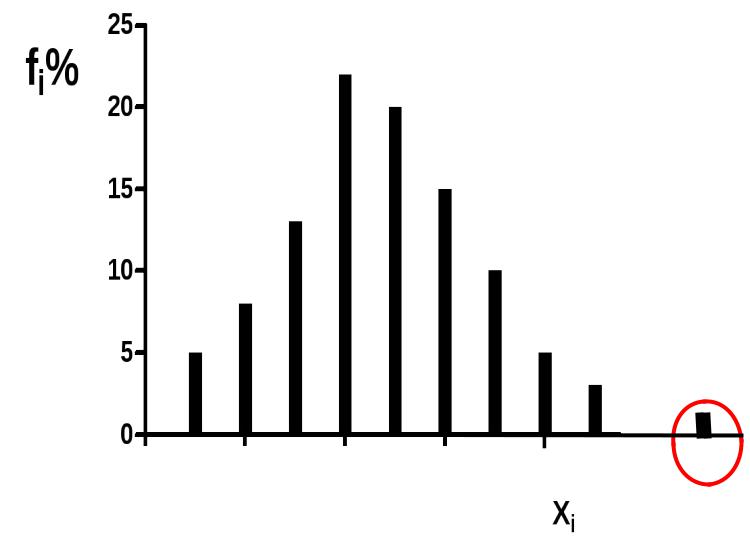
ФОРМИРОВАНИЕ ВЫБОРОК ДЛЯ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ ПРОВЕРКА СОМНИТЕЛЬНЫХ ВАРИАНТ ВАРИАЦИОННОГО РЯДА
?
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
ОБЩАЯ СХЕМА ПОСТРОЕНИЯ КРИТЕРИЯ:
Н0 : сомнительная варианта вместе с другими
принадлежат к одной и той же генеральной совокупности и, следовательно, наблюдаемые отклонения крайних вариант от центра вариационного ряда случайны.
Н1 - варианта относится к другой генеральной совокупности. Н1 формулируется в зависимости от
положения проверяемой варианты в вариационном |
|
ряду: |
min , max |
Критерий строится как односторонний тест
Непараметрические критерии.
1. По разности между сомнительными и соседними
вариантами. |
|
|
Для max ПРОВЕРЯЕТСЯ УСЛОВИЕ: |
|
|
vэксп. ( X n |
X n 1 ) /( X n |
X 2 ) vNst |
N - критерий принадлежности максимальной
варианты к совокупности, XN - максимальная варианта,
XN-1 - варианта, следующая перед максимальной, X - варианта, стоящая в рядом с min
Для2 min ПРОВЕРЯЕТСЯ УСЛОВИЕ:
vэксп. ( X 2 X1 ) /( X n 1 X1 ) vNst
X1 - минимальная варианта.
Квантили критерий табулированы в специальных таблицах.
Вход в таблицу по и n
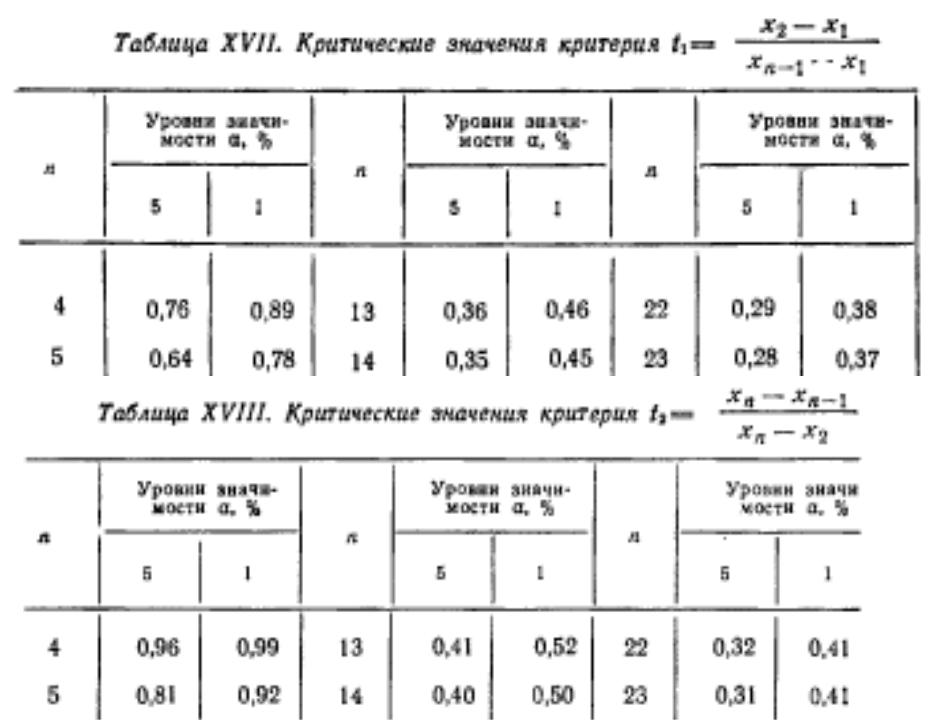
2.По величине среднего квадратического отклонения Статистика критерия:
max |
|
|
vэксп. ( X N |
X N 1 ) / s vNst |
|
|
|
||||
|
|
||||
min |
|
|
|
vэксп. ( X2 |
X1 ) / s vNst |
|
|
|
|||
|
|
|
|||
Квантили критерий табулированы в специальных
таблицах. |
n и |
|
Вход в таблицу по |
Таблица 2Па “Критических значений разности между двумя крайними вариантами совокупности”
(Зайцев, 1984).
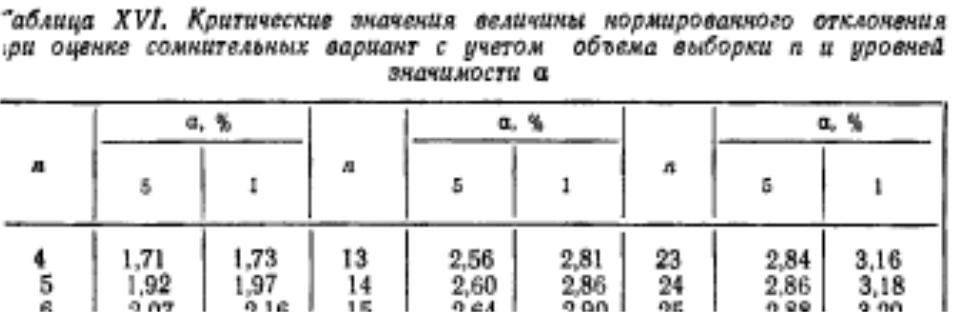
3. Нормальное распределение вариант
Строим наиболее мощный параметрический
критерий t - нормированное отклонение:
ПРОВЕРЯЕТСЯ УСЛОВИЕ:
t = |(Xi-M)/s| =tst .
Квантили критерий табулированы в специальных
таблицах. |
n и |
|
Вход в таблицу по |