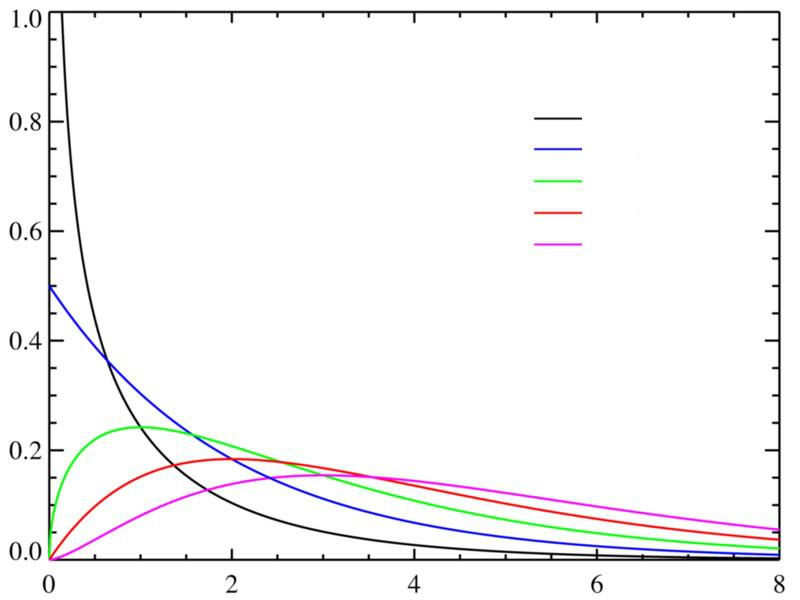
плотность вероятности распределения хи-квадрат
v=1
v=2
v=3
v=4
v=5
v - число степеней свободы
Критерий 2
МЕРА РАССТОЯНИЯ МЕЖДУ МОДЕЛЬЮ И ЭМПИРИЧЕСКИМ РАСПРЕДЕЛЕНИЕМ
k |
(f |
i |
- f |
)2 |
|
2 = i=1 |
|
i |
|
|
|
|
|
|
|
||
|
|
|
fi |
|
|
Где - fi - фактическая частота наблюдений, |
|||||
fi. - ожидаемая (теоретическая). |
частота |
||||
наблюдений, k - число классов. |
|||||
РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ |
2 |
||||
ДОВОЛЬНО БЛИЗКО |
2 |
АППРОКСИМИРУЕТСЯ РАСПРЕДЕЛЕНИЕМ |
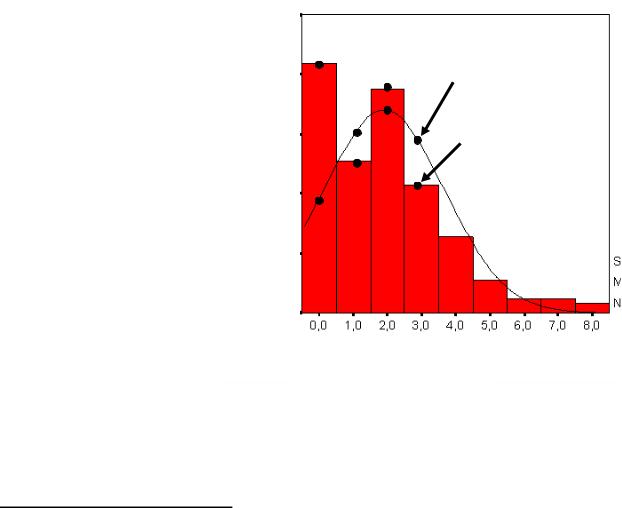
Пример: оценка согласия модели с эмпирическим распределением
H0 : 1 2
0 ,05
H1 : 1 2
ПРОВЕРЯЕТСЯ УСЛОВИЕ СОГЛАСИЯ С НУЛЕВОЙ ГИПОТЕЗОЙ
эксп2 . = k (fi f fi )2 i=1 i
f |
ˆ |
20 |
f |
15 |
fнабл . |
10 |
|
5 |
|
X
st2 ( , )
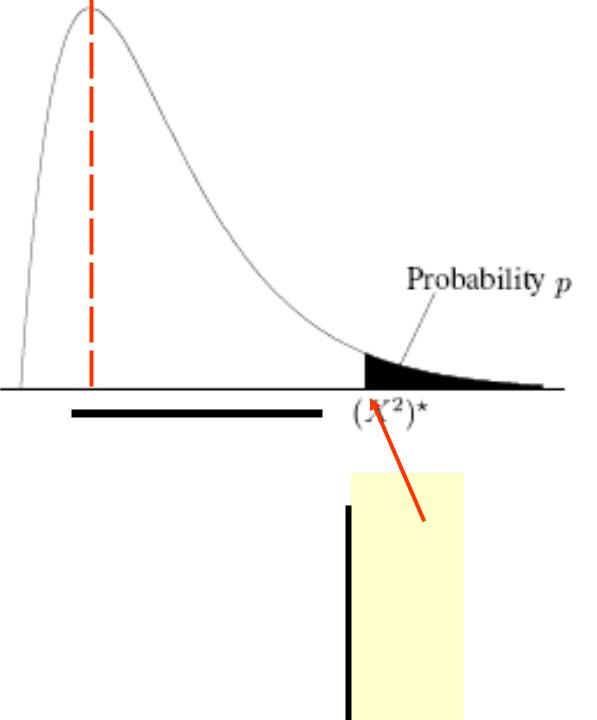
таблицы квантилией распределения хи-квадрат - ОДНОСТОРОННИЕ
? 
df\ |
.995 |
.990 |
.975 |
.950 |
1 |
0.00004 |
0.00016 |
0.00098 |
0.00393 |
2 |
0.01003 |
0.02010 |
0.05064 |
0.10259 |
3 |
0.07172 |
0.11483 |
0.21580 |
0.35185 |
4 |
0.20699 |
0.29711 |
0.48442 |
0.71072 |
5 |
0.41174 |
0.55430 |
0.83121 |
1.14548 |
.050
3.8414
5.9914
7.8147
9.4877
11.071
.025 .010 .005 5.02389 6.63490 7.87944 7.37776 9.21034 10.59663 9.34840 11.34487 12.83816 11.14329 13.27670 14.86026 12.83250 15.08627 16.74960
КРИТЕРИЙ ФИШЕРА (F - СТАТИСТИКА)
Распределение Снедекора-Фишера.
Имеются 2 независимые случайные
~2 ; ~2 ,
Величины 1 2
имеющие распределение хи-квадрат с числом степеней свободы, соответственно 1, ; 2
|
~ |
~2 |
1 |
Тог |
1 |
||
F = |
|
|
|
~2 |
2 |
||
да |
|
2 |
George
W. Snedecor
имеет распределение Снедекора-Фишера, или
F- РАСПРЕДЕЛЕНИЕ.
Sir Ronald
Aylmer Fisher
F - критерий
Р.Фишер вывел закон F-распределения в 1924 г.
Он показал, что
РАЗЛИЧИЯ ГЕНЕРАЛЬНЫХ ДИСПЕРСИЙ ( 12 ; 22 ) ) МОЖНО ИССЛЕДОВАТЬ ПО lg s12 lg s22 ( s12 s22 )
Д. СНЕДЕКОР ДЛЯ СРАВНЕНИЯ ГЕНЕРАЛЬНЫХ
ДИСПЕРСИЙ ПРЕДЛОЖИЛ СТАТИСТИКУ
s2
F s12 F1,v tv2
2
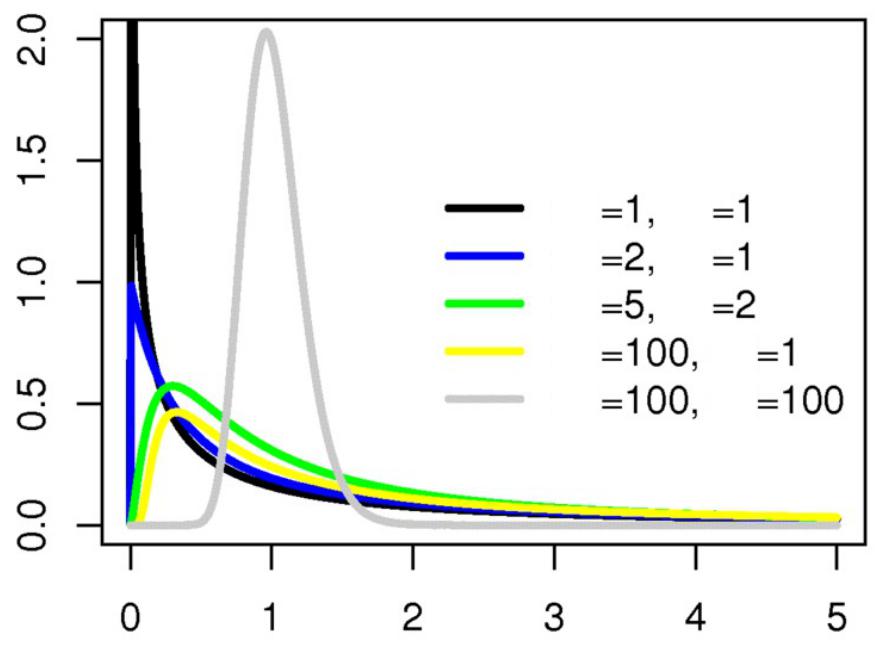
Плотность вероятности распределения Фишера
|
1 |
2 |
|
1 |
2 |
|
11 |
2 2 |
|
||
1 |
2 |
|
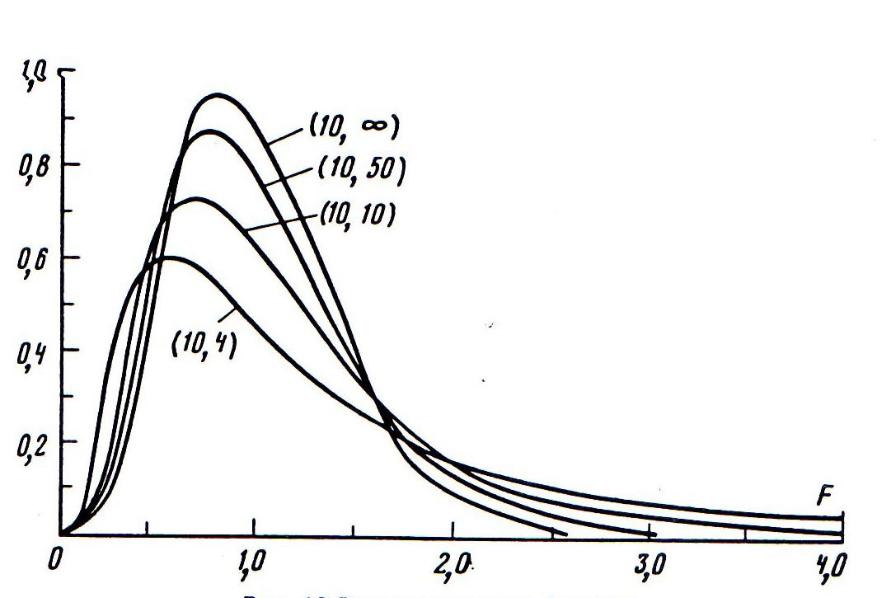
Изменение формы распределения Фишера при фиксированном значении одного из параметров
Пример: |
|
|
2 |
) |
Имеется две выборки из совокупностей |
N1 ( 1 ; 1 |
|||
|
|
|
2 |
) |
нормально распределенных вариант. |
N2 ( 2 ; 2 |
|||
|
|
|||
H0 : 12 22 |
|
|
|
|
, СЛЕДОВАТЕЛЬНО различия |
|
|||
между |
s12 и s22 случайны |
|
||
ПРОВЕРЯЕТСЯ УСЛОВИЕ: |
|
|
|
|
F s12/s22 Fкр. . |
(v 1=n1-1 и v2 n2 -1) |
|
||
0 ,05
H1 : s12 s22 H1 : s12 s22
Строится
односторонний F-критерий
|
|
|
|
|
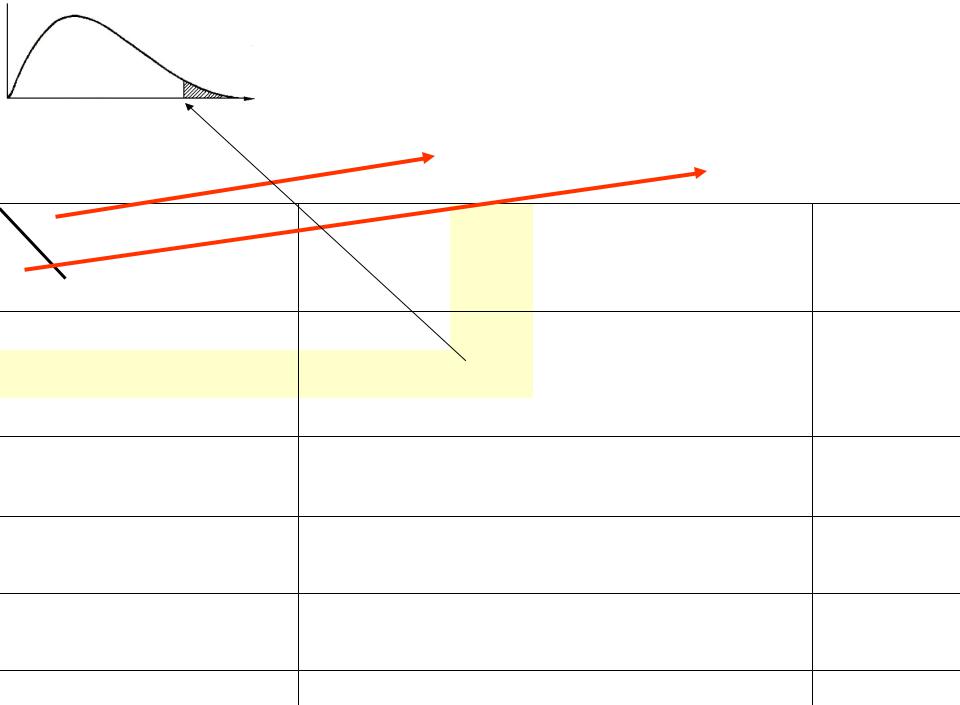
F s2 |
/s2 |
F |
|
|||||
|
|
|
|
|
|
|
1 |
2 |
|
|
кр. |
|
|
0 ,05 |
|
|
(v 1 = n1-1 и v2 = n2 -1) |
|
|||||||||
1 |
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
|
30 |
40 |
50 |
>∞ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
10.13 |
9.55 |
9.28 |
9.12 |
9.01 |
8.79 |
8.70 |
8.66 |
8.62 |
8.59 |
8.58 |
8.54 |
|
4 |
7.71 |
6.94 |
6.59 |
6.39 |
6.26 |
5.96 |
5.86 |
5.80 |
5.75 |
5.72 |
5.70 |
5.63 |
|
5 |
6.61 |
5.79 |
5.41 |
5.19 |
5.05 |
4.74 |
4.62 |
4.56 |
4.50 |
4.46 |
4.44 |
4.36 |
|
6 |
5.99 |
5.14 |
4.76 |
4.53 |
4.39 |
4.06 |
3.94 |
3.87 |
3.81 |
3.77 |
3.75 |
3.67 |
|
7 |
5.59 |
4.74 |
4.35 |
4.12 |
3.97 |
3.64 |
3.51 |
3.44 |
3.38 |
3.34 |
3.32 |
3.23 |
|
8 |
5.32 |
4.46 |
4.07 |
3.84 |
3.69 |
3.35 |
3.22 |
3.15 |
3.08 |
3.04 |
3.02 |
2.93 |
|
9 |
5.12 |
4.26 |
3.86 |
3.63 |
3.48 |
3.14 |
3.01 |
2.94 |
2.86 |
2.83 |
2.80 |
2.71 |
|
10 |
4.96 |
4.10 |
3.71 |
3.48 |
3.33 |
2.98 |
2.85 |
2.77 |
2.70 |
2.66 |
2.64 |
2.54 |
|
15 |
4.54 |
3.68 |
3.29 |
3.06 |
2.90 |
2.54 |
2.40 |
2.33 |
2.25 |
2.20 |
2.18 |
2.07 |
|
20 |
4.35 |
3.49 |
3.10 |
2.87 |
2.71 |
2.35 |
2.20 |
2.12 |
2.04 |
1.99 |
1.97 |
1.84 |
|
>∞ |
1.04 |
3.00 |
2.61 |
2.37 |
2.21 |
1.83 |
1.67 |
1.57 |
1.46 |
1.40 |
1.35 |
1.03 |
|
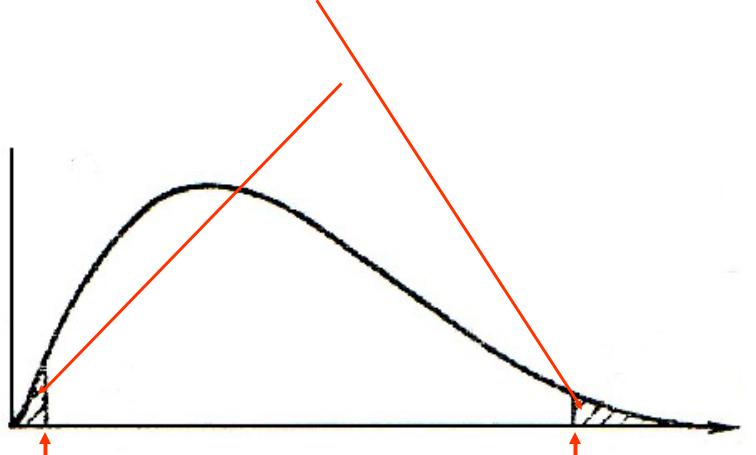
H3 : s12 s22 |
0 ,05 |
|
КРИТИЧЕСКАЯ ОБЛАСТЬ ДЛЯ СЛУЧАЯ |
s12 |
s22 / 2 |
|
2 |
2 |
КРИТИЧЕСКАЯ ОБЛАСТЬ ДЛЯ СЛУЧАЯ |
s1 |
s2 / 2 |
|
|
|
p 0 ,025 |
p 0 ,025 |
|
F2( / 2 ) |
F1( / 2 ) |
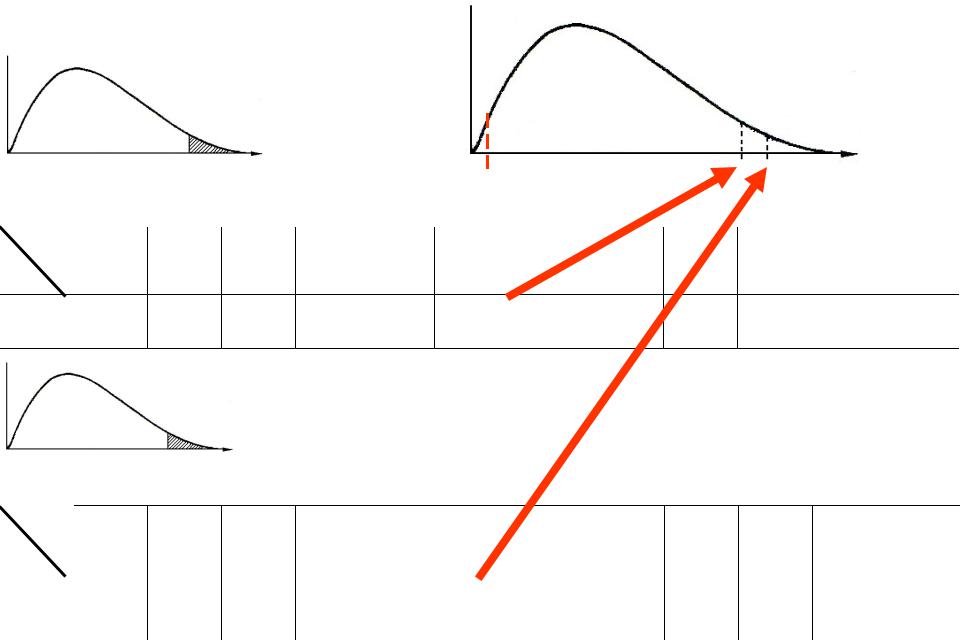
n1 11 |
n2 6 |
H0 : 0 ,05 |
F-критерия |
|
|
|
таблицы |
Таблица F-критерия |
односторонние |
|
0 ,05 ОДНОСТОРОННИЙ
1 |
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
>∞ |
2 |
||||||||||||
5 |
6.61 |
5.79 |
5.41 |
5.19 |
5.05 |
4.74 |
4.62 |
4.56 |
4.50 |
4.46 |
4.44 |
4.36 |
ВХОД В ТАБЛИЦУ0 ,025 ДВУСТОРОННИЙ для /2
2 |
1 |
1 |
2 |
3 |
4 5 |
10 15 20 30 40 50 >∞ |
|
||||||
|
5 |
|
|
|
|
6,62 |