Кононов / 4

Continuous

Fourier Transform Spectroscopy

•All modern IR and Raman spectrometers are done in this way

•Measures all frequencies at same time. More efficient at signal-gathering in a give time (better S/N)

•The frequencies present are deconvoluted (or dispersed) after data is collected.

•Fourier Analysis is the mathematical method for doing this. It is based on the theory that any complex periodic (repeats over time) wave can be decomposed into a linear combination of sinusoids

FT

FT

http://www.wooster.edu/chemistry/is/brubaker/ir/ir_works_modern.html

Types of Optical Instruments

spectroscope – monochromator, detector is eye

photometer – source, filter, photoelectric detector (fluorometer for fluorescence)

spectrometer – source, 's determined by means other than a filter, electronic detector

spectrograph - source, 's determined by means other than filter, photographic film or plate for detector

spectrophotometer – source, 's determined by means other than a filter, photoelectric detector

From: Skoog and Leary, Principles of Instrumental Analysis, p. 111, 4th edition, Saunders College publishing, New York, 1992.

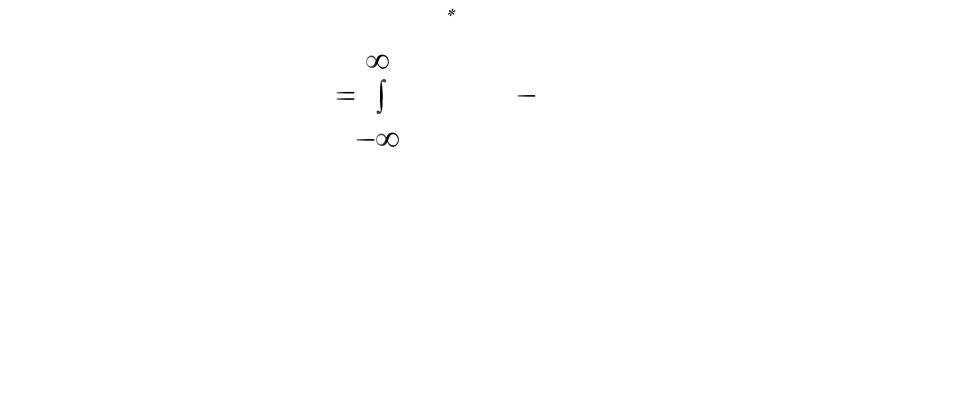
The Instrument Response Function

(аппаратная функция)

Convolution’, n. Origin: Latin: from ‘convolvere’ – ‘roll together’

The convolution of two functions f(x) and g(x) (f g) is given by:

h(x') f (x)g(x' x)dx

OK, but what does that integral actually do…?

1.Sketch f(x)

2.Sketch the other function (g(x)) backwards on a transparency

3.Incrementally slide the transparency across the graph paper in the +x direction

4.At each point (x’) calculate the area under the curve representing the product of the two functions.