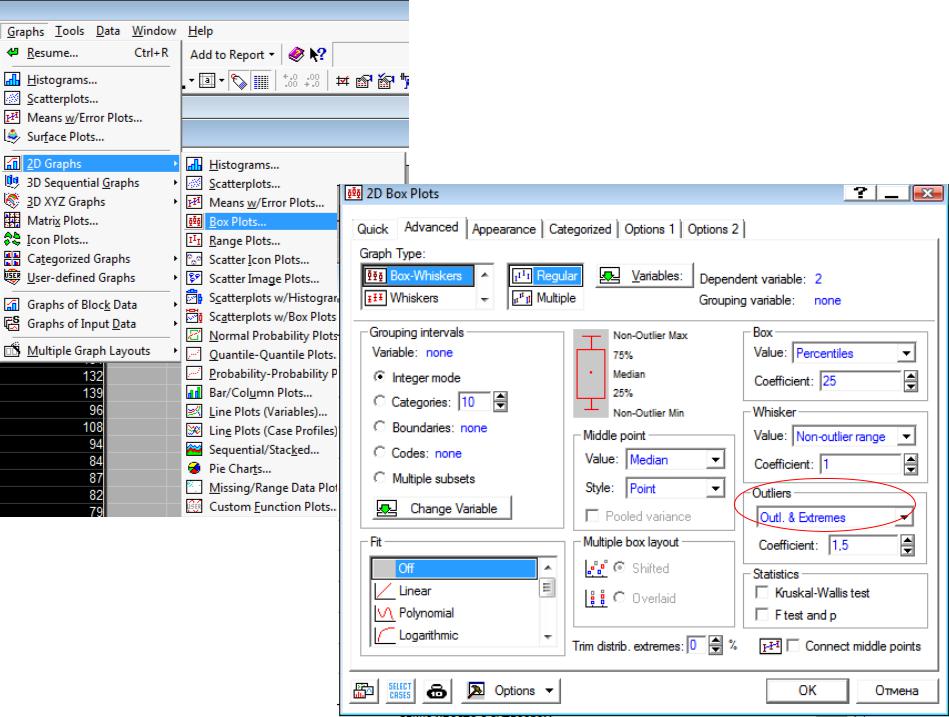
Пакет программ STATISTICA
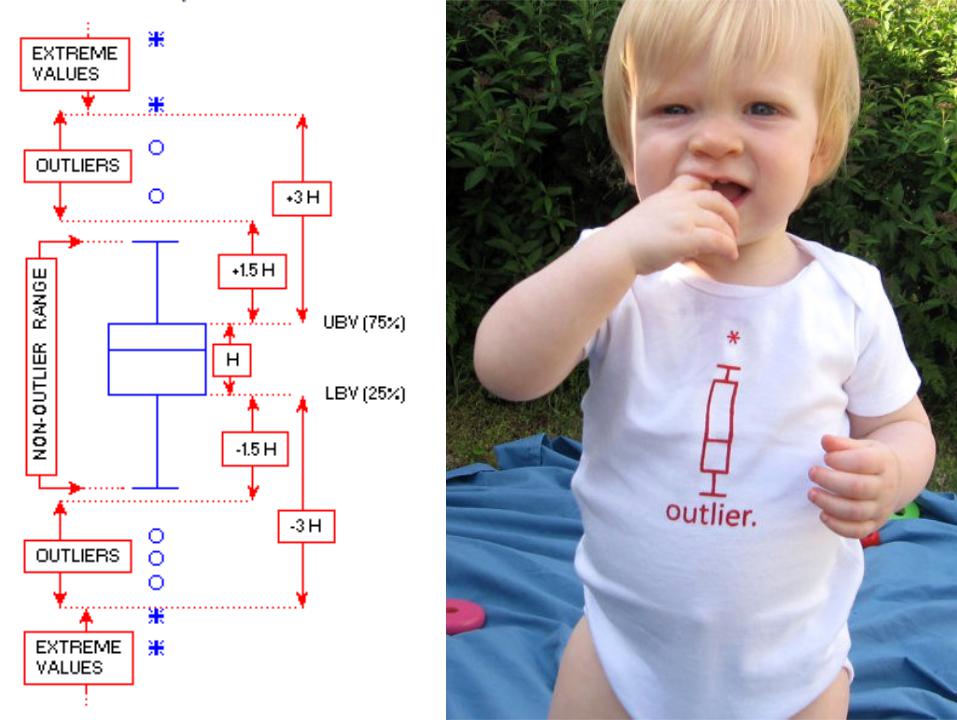
Следует исключить из анализа явные аутлаеры (outliers). Они могут быть заменены ближайшими к ним значениями.
В Statistica аутлаеры –значения, лежащие дальше, чем 1,5 межквартильных размахов выше третьей и ниже первой квартилей.
Экстремы – дальше, чем 3 межквартильных размаха. Аутлаеры – измерения, настолько сильно отличающиеся от остальных, что скорее всего, они не принадлежат к данной выборке. Они сильно сдвигают среднее значение.
Межквартильный размах (Interquartile range ) —
это разность между 75-м и 25-м процентилями упорядоченного вариационного ряда. Межквартильный размах охватывает центральные 50% всех наблюдений выборки.
Аутлаеры
Аутлаеры
аутлаер
Аутлаеры
ОПТИМИЗАЦИЯ ОБЪЕМА ВЫБОРКИ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА.
Мотивация:
-ДОСТИЖЕНИЕ ТРЕБУЕМОЙ ТОЧНОСТИ УЧЕТА;
-ОПРЕДЕЛЕНИЕ ЧИСЛА ИСПЫТАНИЙ ДЛЯ ДОСТИЖЕНИЯ ОПРЕДЕЛЕННОЙ РЕПРЕЗЕНТАТИВНОСТИ ВЫБОРОЧНОГО ПОКАЗАТЕЛЯ;
-ОПРЕДЕЛЕНИЕ ЧИСЛА ИСПЫТАНИЙ ДЛЯ ПОСТРОЕНИЯ КРИТЕРИЯ С ЗАДАННОЙ МОЩНОСТЬЮ;
?
«…всякая попытка
абсолютно точно определить нужный объем выборки бесполезна…"
Дж.У.Снедекор, 1961
СПОСОБЫ ПЛАНИРОВАНИЕ РЕЖИМА ПРОБООТБОРА ПРИ ПОСТРОЕНИИ ПАРАМЕТРИЧЕСКИХ ТЕСТОВ
:
- НАХОЖДЕНИЕ ОБЪЕМА ВЫБОРКИ ПО ВЕЛИЧИНЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА СРЕДНЕЙ;
-НАХОЖДЕНИЕ ОБЪЕМА ВЫБОРКИ С ПОМОЩЬЮ
НЕРАВЕНСТВА ЧЕБЫШЕВА;
-НАХОЖДЕНИЕ ОБЪЕМА ВЫБОРКИ НА ОСНОВАНИИ
ФУНКЦИИ МОЩНОСТИ U-КРИТЕРИЯ;
- НАХОЖДЕНИЕ ОБЪЕМА ВЫБОРКИ НА ОСНОВАНИИ МОЩНОСТИ F-КРИТЕРИЯ ОДНОФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА.
ОПРЕДЕНИЕ НЕОБХОДИМОГО ОБЪЕМА ВЫБОРКИ
Пример: учет численности особей вида выборочных площадках.
Желаемая точность выборочной оценки
– это возможное для принятой вероятности ее отклонение (∆) от генерального параметра
|
t m t s |
|
|||
|
|
|
|
n |
|
n |
t 2 |
s2 |
t 2 s2 |
|
|
|
2 |
|
|
|
|
|
( t m ) |
2 |
|||
|
|
|
|
||
ОПРЕДЕЛЕНИЕ нужного ЧИСЛА УЧЕТНЫХ ПЛОЩАДОК
Точностьучета D = mM / M = s/(M 
n )
По определению выражается в долях от средней (или в %
.
|
|
t s |
2 |
|
|||
n = |
|
|
|
|
|
D M |
|
t - критерий Стьюдента для n=∞;
D’ - необходимая точность учета с учетом t-критерия D’=tm’/M
n( добор ) = n n1
n = |
t2 s2 |
d |
t m |
|
M |
||
d'2 M2 |
Пример: Случайная выборка: n=9, М=12.1, s=2.04;
m=0,68, d=0,68/12,1=0,056(0.06).
Какое число испытаний нужно провести, чтобы увеличить точность учета до 3% (d=0,03)?
2,042 |
4,16 |
|
||
n |
|
|
|
32 |
0,032 12,12 |
0,0009 146,4 |
|||
nиск 32 9 21