Для информации
В стат. пакетах (M)ANOVA реализован разный расчет сумм квадратов.
! Способ расчета суммы квадратов влияет на результаты многофакторного
дисперсионного анализа для выборок НЕОДИНАКОВОГО объема.
Тип I. Метод иерархической декомпозиции сумм квадратов. Сбалансированной модели дисперсионного анализа, Полиномиальной регрессионной модели, Чисто гнездовой модели
Тип II. Вычисляет суммы квадратов эффекта в модели, скорректированные по всем остальным "подходящим" эффектам:
Сбалансированной модели дисперсионного анализа.
Любая модель, которая содержит только главные эффекты факторов. Любая регрессионная модель.
Модели гнездового плана.
Тип III. Задается по умолчанию..
Любых моделей, перечисленных для типа I и типа II.
Любой сбалансированной или несбалансированной модели без пустых ячеек.
Тип IV (SPSS). Этот метод разработан для случая, когда есть пустые ячейки. Любые модели, перечисленных для типа I и типа II.
Любой сбалансированной или несбалансированной модели с пустыми ячейками.
Формирование сумм квадратов отклонений 1, 2, 3 типов плана дисп. анализа для двух факторов А и В.
Модель может содержать два главных эффекта факторов А и В и эффект взаимодействия АВ.
Эффект |
1 способ |
2 способ |
3 способ |
(sstype=1) |
(sstype=2) |
(sstype=3) |
|
A |
R(1)-R(A) |
R(B)-R(A,B) |
R(B,AB)-R(A,B,AB) |
B |
R(A)-R(A,B) |
R(A)-R(A,B) |
R(A,AB)-R(A,B,AB) |
AB |
R(A,B)-R(A,B,AB) |
R(A,B)-R(A,B,AB) |
R(A,B)-R(A,B,AB) |
|
|
|
|
Порядок эффектов соответствует последовательности: А, В, АВ. Величина R(·) представляет остаточную сумму квадратов отклонений для модели:
R(A,B,AB) - остаточная сумма квадратов соответствующая полной модели, R(A) - остаточная сумма квадратов соответствующая главному эффекту фактора А,
R(1) - остаточная сумма квадратов соответствующая общему среднему арифметическому.
В Statistica и SPSS можно выбрать способ расчета сумм квадратов
Непараметрические критерии
Критерий Краскела-Уоллиса: ранговый - проверка однородности при одном факторе
определение неоднородности нескольких выборок при одном
действующем факторе
Критерий Джонкхиера для альтернатив с упорядочением
вариант критерия Манна-Уитни для случаев нескольких
выборок
Критерий Фридмана : ранговый - проверка однородности комплекса при двух факторах
то же, что и статистика Краскела-Уоллеса,
но при двух действующих факторах.
Критерий Пейджа для альтернатив с упорядочением
Вариант дисперсионного анализа рангов
ПРИКЛАДНАЯ ЗАДАЧА:
МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ ПОКАЗАТЕЛЯ?
ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ: ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ СРЕДНИХ (О ПРИНАДЛЕЖНОСТИ СРЕДНИХ К ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ)
НОРМАЛЬНЫЙ ЗАКОН |
РАСПРЕДЕЛЕНИЕ НЕ |
|
|
||
КРИТЕРИИ: |
НОРМАЛЬНОЕ, ИЛИ |
|
НЕЧИСЛОВАЯ ШКАЛА |
||
- ШЕФФЕ. |
||
|
||
-ДИКСОНА. |
|
|
- ДИСПЕРСИОННЫЙ |
КРИТЕРИИ: |
|
АНАЛИЗ, |
- КРАСКЕЛА-УОЛЛИСА. |
|
- LSD |
- МЕДИАННЫЙ, |
|
(LEAST SIGNIFICANT |
- РАНГОВЫХ СУММ |
|
DIFFERENCE ) |
ФРИДМАНА |
ПРИКЛАДНАЯ ЗАДАЧА:
МОЖНО ЛИ СЧИТАТЬ, ЧТО В НЕСКОЛЬКИХ ВЫБОРКАХ ИМЕЕТ МЕСТО ОДНО И ТО ЖЕ ЗНАЧЕНИЕ РАССЕИВАНИЯ ПОКАЗАТЕЛЯ?
ЗАДАЧА СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ:
ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДИСПЕРСИЙ (О ПРИНАДЛЕЖНОСТИ
ДИСПЕРСИЙ К ОДНОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ)
НОРМАЛЬНЫЙ ЗАКОН |
РАСПРЕДЕЛЕНИЕ |
|
|
НЕНОРМАЛЬНОЕ, ИЛИ |
|
КРИТЕРИИ: |
НЕЧИСЛОВАЯ ШКАЛА |
|
|
||
- G-КРИТЕРИЙ (КОХРЕНА) |
КРИТЕРИИ: |
|
-БАРТЛЕТА |
||
- ФРИДМАНА |
||
(ПРИ РАВНОМ РАЗМЕРЕ ВЫБОРОК ) |
||
|
- ЛЕВЕНЕ |
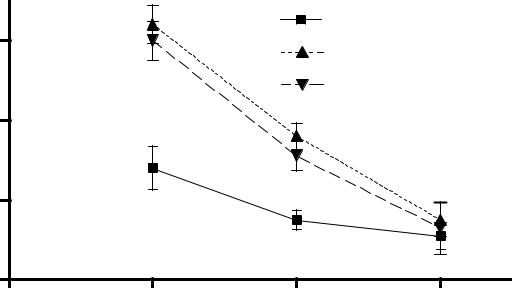
Итак Но гипотеза отвергнута в пользу Н1, и
фактор значимо влияет на переменную.
Однако какие именно выборки отличаются друг от друга. Чтобы узнать это, достаточно выполнить следующее:
1. Градиентные построения по итогам дисперсионного анализа
L
8 |
III |
- |
A |
|
- |
B |
|||
|
|
|||
|
|
- |
C |
|
6 |
|
|
|
4
2 |
|
|
t |
|
0 |
1 |
2 |
3 |
Вариация средних величин годового прироста L. saxatilis на станции у о.Ряжков при изменении возраста и места сбора (А – верхний, В – средний и С – нижний горизонты литорали) моллюсков.
По оси ординат – прирост, мм; по оси абсцисс – возраст моллюсков (годы)
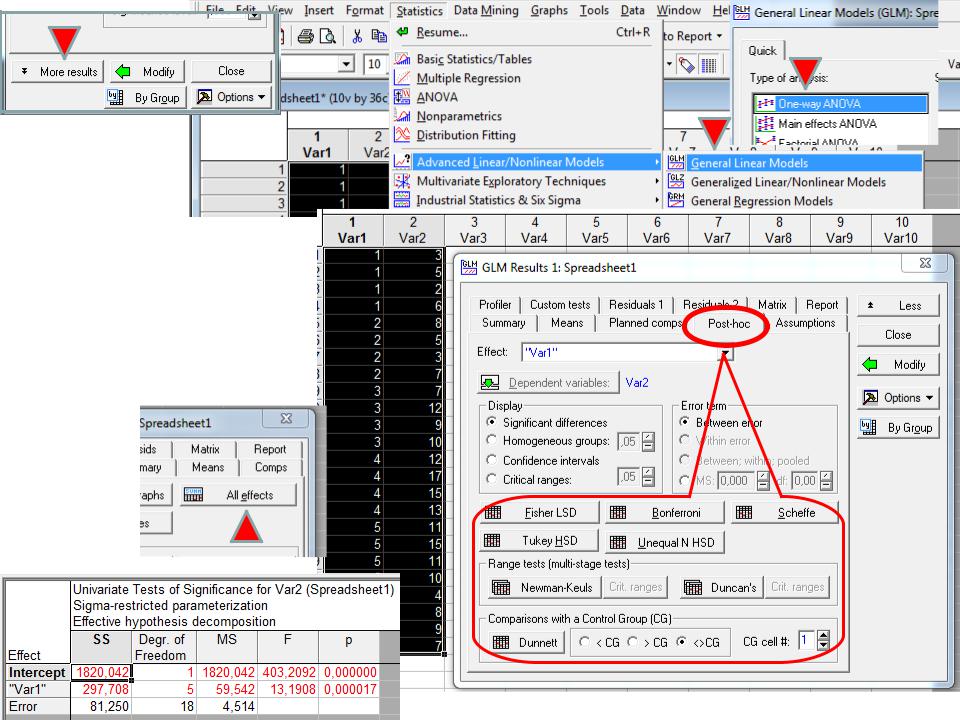
ANOVA post hoc tests
Fisher test (Least Significant Difference)
Bonferroni correction – очень консервативный тест, который нельзя
использовать для большого (>8) числа выборок. Иначе мы резко снижаем мощность критерия.
Scheffé's test - критерий Шеффе,поверяет не только парные гипотезы, но и
комплексные.
Newman–Keuls test - Критерий Ньюмена-Кейлса (Newman-Keuls test) - наименее
строгий. Все средние упорядочивают по возрастанию и вычисляют критерий; начинают от сравнения наибольшего с наименьшим.
Dunnett's test - Критерий Даннетта, используется для сравнения нескольких
групп с контрольной группой.
False discovery rate
Duncan's new multiple range test
Rodger's method
TUKEY'S RANGE TEST - Наиболее распространённый и рекомендуемый в литературе для близких по размеру групп. Проверяет только ПАРНЫЕ гипотезы.
4в |
2 |
3 |
|
|
ПРИМЕР:
Однофакторный |
|
|
равномерный |
1 |
|
комплекс: |
||
|
||
N=24 |
|
|
m= 6 |
5в |
|
ni=4 |
||
4а |
|
5а
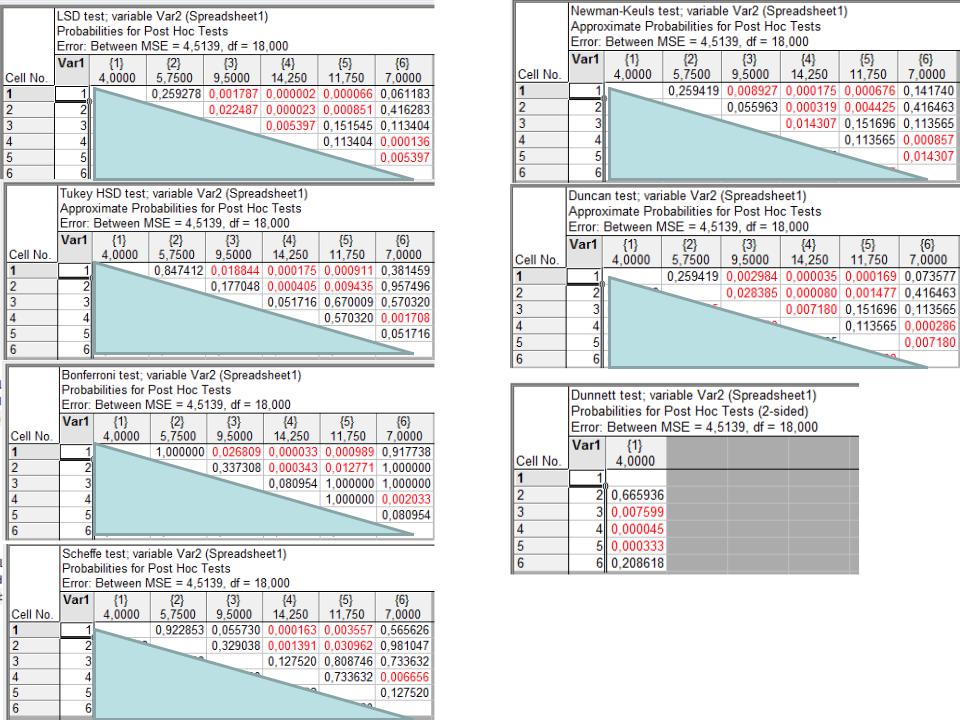
Фишера |
Ньюмена-Кеулса |
|
Тюкей
Дункана
Даннетта
Бонферрони
Statistica
Post-hoc тесты
Шеффе