Понятие случайного вектора.

В прикладных задачах часто приходится рассматривать не одну случайную величину, а несколько, наблюдаемых одновременно в эксперименте.

Определение. Совокупность случайных величин Х₁ , Х₂ , … Х_n , заданных на одном и том же вероятностном пространстве (,A, Р), называются n-мерным случайным вектором или n-мерной случайной величиной. Сами случайные величины называются при этом координатами случайного вектора.При n=2 случайная величина называется двумерной. Мы ограничимся рассмотрением этого случая.

Итак,

Пара случайных величин (X,Y) (или (ξ,η) , заданных на одном вероятностном пространстве. называется двумерной случайной величиной (двумерным случайным вектором)

Когда речь идет о двух случайных величинах, мы можем интересоваться распределением каждой из них «самой по себе», а также условным распределением (одной, при условии, что вторая приняла какие-то значения).

Соответствующее распределение случайного вектора называется совместным распределением.

(Совместная) функция распределения F(a₁,a₂)=P{X< a₁, Y< a₂} в данном случае есть вероятность попасть в квадрант , верхним правым углом которого является точка (a₁,a₂)

Рис.6

Определение. Двумерная величина (X,Y) называется дискретной, если дискретной является каждая из величин Х и Y. Мы ограничимся рассмотрением случая двумерной дискретной случайной величины.

Определение. Две случайные величины

Х= {x₁,x₂,,x_n};Y= {у₁, у₂,,у_m},

определённые на одном и том же пространстве элементарных исходов, имеющие законы распределения

X	х1		xi			Y	y1		yj	
Р						Р				

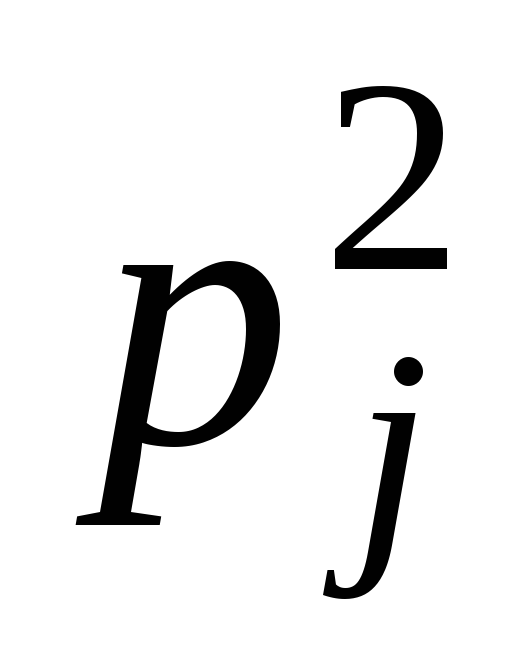
(верхние индексы – это не степени, а указатель на принадлежность той или иной случайной величине)

называются независимыми, если при любыхiи jвыполняется равенство

Р((X = х_i) ∩(Y = y_j)) =

Замечание. В общем случае, случайные величины независимы, если совместная функция их распределения равна произведению функций распределения X и Y.

Или, в терминах вероятности, P(X<x, Y<y) = P(X<x)  P(Y<y)

Пример.Брошены две игральных кости. Число очков, выпавшее на первой кости, – случайная величинаХ. Число очков, выпавшее на второй кости – случайная величинаY. Считаем, что все исходы ((X=i)∩(Y=j)) (i= 1,2,,6;j= 1,2,,6) равновероятны, всего их 36 (см Тема 1), поэтому

P((X=i)∩(Y=j)) =

Так как P(X=i) =иP(Y=j)) =, очевидно, что по определениюXиY– независимые случайные величины.

Пример 2. Даны две независимые случайные величины Xи Yс заданными законами распределения

X	0	1		Y	1	2
Р				Р

Определим случайные величины  и  следующим образом:  = X+Y,  = XY. Выясним, являются ли независимыми случайные величины и .

Составим закон распределения .

	1	2	3			0	1	2
Р	1/12	2/12+3/12=5/12	6/12=1/2		Р	1/12+3/12=1/3	2/12=1/6	6/12

Наименьшее значение  равняется 1. Вероятность события  = 1 равна вероятности события (X= 0)∩(Y= 1), которая в силу независимостиXиYравна. Событие = 2 совпадает с событием ((X= 0)∩(Y= 2)) + ((X= 1)∩(Y= 1)). Его вероятность равна

.

Максимальное значение , равное 3, имеет вероятность .

Рассмотрим события  = 3 и  = 0. Очевидно, что

Р( = 3) Р( = 0) = 

С другой стороны, событие ( = 3)∩( = 0) – невозможное, так как  = 3 только при X= 1, а = 0 лишь при X= 0. Отсюда следует, что

Р((= 3)∩(= 0)) = 0,