Примеры дискретных распределений

Равномерное распределение

Дискретная величина принимает конечное число значений с одинаковыми вероятностями. Например, случайная величина принимает значение числа на верхней грани кубика при однократном подбрасывании

Х	х1	х2	х3		хn
P				

Биномиальное распределение

Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний .p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1

P{X =i} =

Сумма в нижней строке есть биномиальное разложение для (p+q)ⁿ =

Отступление. О Биноме Ньютона

Бином Ньютона – это формула возведения суммы в степень с натуральным показателем.

Геометрическое распределение

Случайная величина принимает значение числа неудач до первого успеха в в схеме Бернулли, p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1. Испытания независимы, поэтому по правилу умножения вероятностей

, как сумма бесконечно убывающей геометрической прогрессии

Распределение Пуассона

Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний: Х=0,1,2,…,n…, p – вероятность успеха, успехи редки, их вероятность мала. n∙p=λ>0 – параметр распределения

- сумма ряда Тейлора для экспоненты

Раздел 1.4.3. Понятие случайной величины с абсолютно непрерывным законом распределения

Определение. Случайная величина, принимающая несчетное число значений (значения которой заполняют некоторый промежуток) и имеющая плотность, называется случайной величиной с абсолютно непрерывным законом распределения или (абсолютно) непрерывной случайной величиной..

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу­бесконечными или бесконечными, например: (a; b], (– ; a), [b;), (–; ).

При описании непрерывной случайной величины невозможно выписать и пронумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество.

Замечание. Вернемся к нашей аналогии со стержнем. Теперь на нем не точечные массы, а сам он представляет собой стержень переменной плотности, протянувшийся от наименьшего до наибольшего значения случайной величины. Очевидно, что вопрос о массе в конкретной точке теперь невозможно поставить, а можно лишь говорить о массе, распределенной в некотором объеме (на некотором участке нашего стержня).

Таким образом, вместо вероятности-массы мы получаем плотность (вероятности). Из-за схожести физической и вероятностной плотности последнюю чаще всего обозначают, как в физике, буквой ρ (греческая ро). Другой распространенный вариант – р – подчеркивает связь с вероятностью.

Замечание. Если Х – непрерывная случайная величина, то равенство Х = х представляет собой, как и в случае дискретной случайной величины, некоторое случайное событие, но для непрерывной случайной величины это событие можно связать лишь с вероятностью, равной нулю, что, однако, не влечёт за собой невозможности события. Поэтому, применительно к абсолютно непрерывным случайным величинам, говорят только о вероятности попасть в промежуток.

Пусть Х – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность неравенства х < Х < х + х

P(х < Х < х + х).

Здесь х – величина малого интервала.

Очевидно, что если х  0, то P(х < Х < х + х)  0. Обозначим (х) предел отношения P(х < Х < х + х) к при х  0, если такой предел существует:

Функция (х) называется плотностью распределения случайной величины. Из этой формулы следует равенство, справедливое для малых величин х, которое также можно считать определением функции (х):

P(х < Х < х + х) (x)х

Очевидно, что (x) – неотрицательная функция. Для определения вероятности того, что случайная величина Х примет значение из промежутка [a, b] конечной длины, нужно выбрать на промежутке произвольные числа x₁, х₂,,  х_n удовлетворяющие условию а=х₀<х₁<x₂<<x_n<b=x_n+1. Эти числа разобьют промежуток [a, b] на n+1 частей, представляющих собой промежутки [х₀, х₁), [х₁, х₂), ,[х_n, b]. Введём обозначения:

х₀= х₁ – х₀, х₁= х₂ – х₁, , х_n = b – х_n,

и составим сумму. Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величинах_i стремится к нулю. Будем считать функцию  (x) непрерывной на промежутке (а; b), тогда пределом суммы будет определённый интеграл по промежутку [a; b] от функции p(x), равный искомой вероятности:

P(a  Х  b) = (3)

З

Рис. 1

амечание. Это равенство можно также рассматривать как определение функции  (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х₁, х₂) равна площади фигуры, образованной отрезком [х₁, х₂] оси х, графиком функции (х) и вертикальными прямыми х = х₁, х = х₂, как изображено на рисунке 1.

Замечание. С другой стороны, вероятность попасть в промежуток есть разность значений функции распределения на концах промежутка.

Если все возможные значения случайной величины принадлежат интервалу (а; b), то для  (х) – её плотности распре­деления справедливо равенство

Для удобства иногда считают функцию (х) определённой для всех значенийх, полагая её равной нулю в тех точкахх, которые не являются возможными значениями этой случайной величины.

Плотностью распределения может служить любая интегрируемая функция (х), удовлетворяющая двум условиям:

1. (х)  0;

2. 

Определение. Законом распределения непрерывной случайной величины является ее плотность.

Можно задавать случайную величину, задавая функцию (х), удовлетворяющую этим условиям.

В качестве примера рассмотрим случайную величину Х, равномерно распределённую на промежутке [a; b]. В этом случае (х) постоянна внутри этого промежутка:

По свойству 2) функции (х)

О

Рис. 2

тсюда. График функции

 (х) представлен на рисунке 2.

Замечанание. Во многих практических задачах встречаются случайные величины, у которых возможные значения не ограничены сверху и снизу. В этом случае кривая распределения располагается над осью х и при х   и х  –  асимптотически приближается к этой оси, как изображено на рисунке 1. Вероятность того, что случайная величина Х примет значение, меньшее некоторого числа а, равна площади фигуры, заключённой между кривой распределения и горизонтальной координатной осью слева от точки а. Будем считать, что такая площадь существует.

Напоминание. Пусть Х – непрерывная случайная величина. Функция F(x), которая определяется равенством

,

называется интегральной функцией распределенияили простофункцией распределенияслучайной величиныХ. Непосредственно из определения следует равенство. Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению. Плотность распределения(х) называютеще дифференциальной функцией распределения.

Замечание. Определение. Иногда плотность (закон распределения) определяют «в обратную сторону»: Плотность есть подинтегральная функция функции распределения абсолютно непрерывной случайной величины.

.

Замечание. Таким образом, если известна плотность распределения случайной величины, для нахождения функции распределения необходимо взять от нее указанный выше интеграл, а если, наоборот, известна функция распределения, то плотность находится дифференцированием (взятием производной) этой функции.

Нахождение неизвестного параметра плотности находится с помощью свойства 2) – равенства 1 интеграла от плотности по всей числовой оси.

Например, если на всей оси Х (х) = 2С / (1 + x²) Найти С. Рассмотрев интеграл от  по всей оси, получим С = 1/2

Отступление.

Интеграл с переменным верхним пределом

Для функции f(x), интегрируемой для всех x a, значение интеграла зависит от значения верхнего пределаx; можно рассмотреть функцию переменной x: каждому значению x ставится в соответствие число, равное значению интеграла . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела:; функция Ф(х) определена в области интегрируемости подынтегральной функцииf(x),. Если F(x)первообразная для f(x), то значение Ф(х)можно вычислить по формуле Ньютона-Лейбница :

.

Функцию

можно исследовать, не вычисляя первообразной. Для интегрируемой при x  a функции f(x), справедливы следующие утверждения: Ф(х)непрерывна на промежутке [a, ∞), причем Ф(а) = 0; если f(x)>0, при х  а, то    Ф(х)монотонно возрастает на промежутке [a, ∞); если f(x), непрерывна при х  а, то Ф(х) дифференцируема на промежутке [a, ∞), причем

Замечание. То обстоятельство, что производная от интеграла с переменным верхним пределом есть подинтегральная функция, является одним из ключевых в математическом анализе. Это свойство интеграла с переменным верхним пределом является связующим звеном между дифференциальным и интегральным исчислением.

Отступление.

Несобственный интеграл

Пусть функция y = f(x) определена и непрерывна на полубесконечном промежутке [a;), тогда интегралс бесконечным верхним пределом (несобственный интеграл) понимается как , еслиэтот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.

Аналогично

и

Функция распределения F_Х(x) случайной величины Х имеет следующие свойства.

1. F_Х(x) — непрерывная возрастающая функция.

2. ;

Свойства 1 и 2 вытекают непосредственно из определения функции F(x).

3. Приращение F(x) на промежутке (х₁; х₂) равно вероятности того, что случайная величина Х принимает значение из этого промежутка:

F(x₂) – F(x₁) = P(x₁ Х < x₂)

Доказательство.

F(x₂) = P(Х < x₂) = P(Х < x₁) + P(x₁  Х < x₂) = F(x₁) + P(x₁ Х < x₂)

Отсюда

P(x₁ Х< x₂) = F(x₂) –F(x₁)

Для равномерного распределения функция F(x) имеет вид:

Рис. 3

График функции F(x) представлен на рисунке 3.

Закон распределения непрерывной случайной величины можно определить заданием либо функции  (х), либо функции F(x).

Примеры абсолютно непрерывных распределений.

Равномерное непрерывное распределение было рассмотрено выше

Экспоненциальное распределение. Это распределение с плотностью ρ(х)=

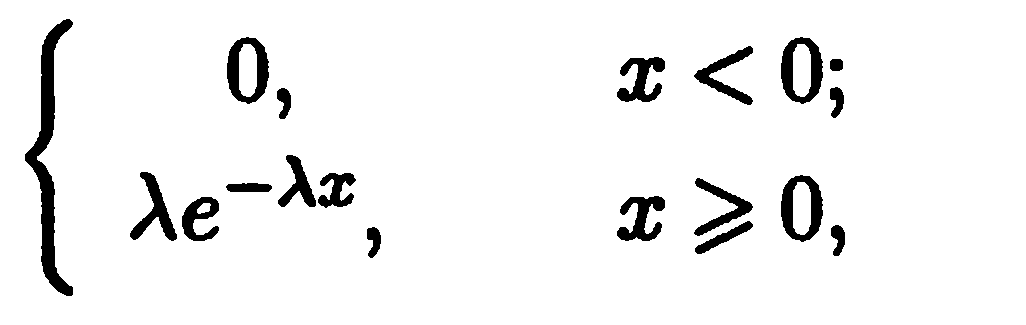, λ > 0 – параметр экспоненциального распределения, его

функция распределения имеет вид

Плотность Функция распределения

Рис.4

Экспоненциальное распределение возникает как предельный вариант геометрического распределения. В качестве успехов и неудач рассматривается, произошло ли событие А в течение (стремящихся к нулю) промежутков времени.

Нормальное распределение.

Случайная величина имеет нормальный закон распределения c параметрами, m и σ², N (m, σ²) если ее плотность имеет вид

А функция распределения, соответственно,

Если m=0, σ =1, распределение называется стандартным нормальным законом. Плотность в этом случае – уже известная функция Гаусса.

Поэтому в случае нормального закона плотность и функция распределения обозначаются φ и Ф, а не ρ и F.

Рис. 5

Как следует из этих рисунков, параметр m определяет положение центра симметрии плотности нормального распределения, а σ – разброс значений случайной величины относительно центра симметрии. И, соответственно,

высоту и «крутизну» пика графика плотности (чем больше σ, тем ниже пик и медленнее стремление к нулю)

К абсолютно непрерывным распределениям относятся также крайне важные в статистической практике распределения χ² и Стьюдента. Но ввиду сложности формул этих распределений (они содержат гамма-функцию Эйлера), мы не будем их здесь приводить.