Курс статистики / Модуль 2. Лекции / Тема 2.5. Элементы регрессинного анализа

Тема 2.5.

Элементы регрессионного анализа

Постановка задачи.

Метод наименьших квадратов.

Пример

После обнаружения стохастических связей между изучаемыми переменными величинами (корреляционный анализ) приступают к математическому описанию интересующих зависимостей. Для этого необходимо решить следующие задачи:

1) подобрать класс функций, в котором целесообразно искать наилучшее приближение искомой зависимости;

2) найти оценки для неизвестных значений параметров, входящих в уравнение искомой зависимости;

3) установить адекватность полученного уравнения искомой зависимости;

4) выявить наиболее информативные входные переменные (факторы).

Совокупность перечисленных задач и составляет предмет

исследований регрессионного анализа.

Мы будем рассматривать самый простой случай так называемой простой линейной модели, когда предполагается линейная зависимость между величинами и задача состоит в отыскании оценок коэффициентов функции y=kx+b

Коэффициент корреляции описывает зависимость между двумя случайными величинами одним числом, а регрессия выражает эту зависимость в виде функционального соотношения, и поэтому дает более полную информацию. Например, регрессией является средний вес человека как функция от его роста. Термин «регрессия» впервые был введен Ф.Гальтоном, изучавшим наследование количественных признаков. Он обнаружил, что у высоких (низких) родителей рост детей обычно выше (ниже) среднего, но не совпадет с ростом родителей. Линия, показывающая, в какой мере рост (и другие характеристики)регрессируют (возобновляются, возвращаются) в среднем в последующих поколениях, была названа Ф.Гальтоном линией регрессии.

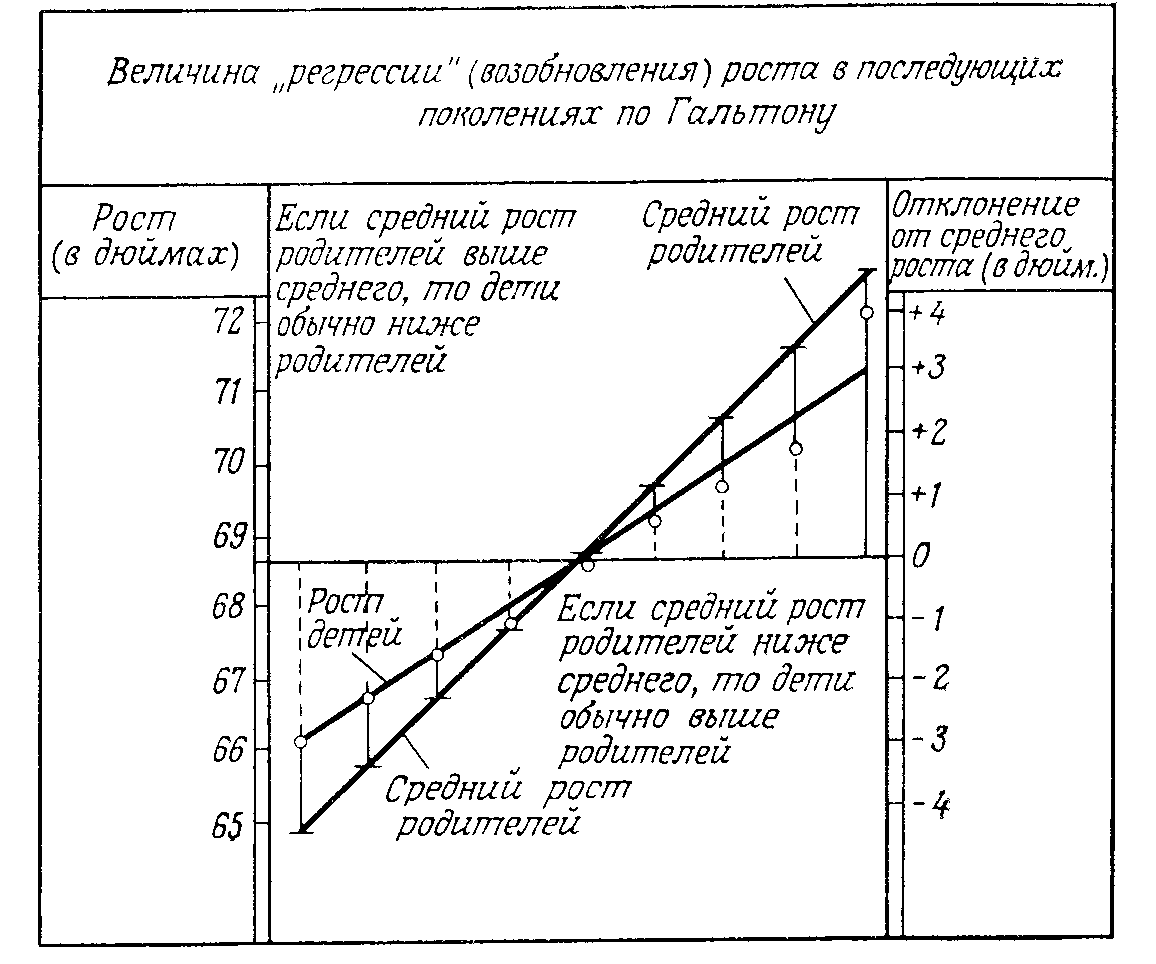
Рис 1.Линия регрессии Гальтона

Со временем этот термин утратил свое первоначальное значение и стал применяться и для обозначения изменения функции в зависимости от изменения одного или нескольких аргументов, то есть так стали называть любую функциональную зависимость между случайными величинами.

Отличие статистической связи от функциональной заключается в том, что в последнем случае между аргументом и функцией существует однозначное соответствие, то есть каждому значению переменного х соответствует однозначно y=f(x). При статистической связи разным значениям одной переменной соответствуют различные распределения другой переменной.

Итак, связь между аргументами можно выразить как зависимость Y=f(X) X=g(Y). Изменение функции при изменении одного или нескольких аргументов называется регрессией.

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимой переменной (переменным) (Х) . То есть, в нашем случае простой линейной модели задача состоит в том, чтобы оптимальным (в вышеуказанном смысле) способом «проложить» прямую через диаграмму рассеяния.

Регрессию выражают с помощью двух уравнений регрессии, которые в случае линейной модели имеют вид уравнений прямой:

Y = a₀ + a ₁X

X = b₀ + b₁ Y

Напоминание:

Уравнение y = kx + b – уравнение линейной зависимости. Оно задает уравнение прямой. Здесь х – независимая переменная, y – зависимая, k – угловой коэффициент (тангенс угла наклона прямой), определяет угол наклона прямой по отношению к оси ОХ, b – свободный член, определяет насколько единиц сдвинут вдоль оси OY график «исходной» функции y=kx.

Рис. 2. Пример линий регрессии

Линии регрессии пересекаются в точке О, с координатами, соответствующими средним арифметическим значениям переменных X и Y. Линия АВ, проходящая через точку О, соответствует линейной функциональной зависимости между переменными Х и Y. Коэффициент корреляции в таком случае равен 1. При этом наблюдается такая закономерность: чем сильнее связь между Х и Y, тем ближе обе линии регрессии к прямой АВ, и, наоборот, чем слабее связь между этими величинами, тем больше линии регрессии отклоняются от этой прямой. При отсутствии линейной связи между Х и Yоказываются под прямым углом друг к другу, что соответствует равенству нулю коэффициента корреляции. Регрессионный анализ в таком случае сводится к определению коэффициентов a₀ , a ₁, b₀ и b₁ и определению уровня значимости полученных аналитических выражений.

Замечание. Вообще говоря, к этому сводится любой вид регрессионного анализа с поправкой на количество переменных и вид функциональной зависимости.

Сложность заключается в том, что в реальности, даже если мы предполагаем линейную зависимость, уравнение зависимости для каждого значения переменной выглядит так:

y_i = a ₁x_i + a₀ + ε_i , то есть решение определяется с точностью до коэффициента , то есть не является однозначным. Коэффициент  - случайная суммарная ошибка – отклонение конкретной экспериментальной точки от искомой прямой, то есть свой для каждого i .Если предположить, что для эти коэффициенты независимы и нормально распределены( а для этого, как мы обсудили в теме «последовательность независимых величин», есть основания), задача состоит в построении такой прямой, чтобы суммарный разброс отклонений – то есть дисперсия ε_i , была бы минимальной. Что в конечном итоге означает минимизацию суммы квадратов коэффициентов ε_i . Метод, позволяющий достичь этого, называется методом наименьших квадратов.

Отступление. Основа метода наименьших квадратов

В основе метода наименьших квадратов лежит так называемый принцип Лежандра: Сумма квадратов отклонений наблюдаемых значений от искомой оценки должна быть минимальной.

Пусть даны три точки на числовой оси: a,b,c. Зададим зависящую от х функцию формулой f(x) = (x-a)² + (x-b)² +(x-c)² , где (x-a)^, , (x-b)² , (x-c)² – квадраты расстояний от точек a, b и c до x. Мы хотим определить, при каком значении х эта функция минимальна? Подобные задачи (поиск экстремума) решаются с помощью поиска производной функции f(x), которая в этом случае равна f(x) = 6x – 2a– 2b–2c. Равенство нулю производной – необходимое условие экстремума, в данном случае минимума, – достигается в одной точке – x = (a+b+c)/3.

При применении метода наименьших квадратов минимизация ведется вдоль оси Y, количество рассматриваемых точек совпадает с числом наблюдений n

Первое теоретико-вероятностное обоснование метода наименьших квадратов дано в работах Гаусса в 1809 и 1821 гг. В более общем виде теорема Гаусса о свойствах оценок наименьших квадратов сформулирована и доказана А. Марковым в 1912 г.

Метод наименьших квадратов работает при условии выполнения следующих предположений:

1. Общий вид зависимости известен, причем эта зависимость линейна по некоторым неизвестным параметрам a₀, a₁

2 Ошибки измерения ε_i случайны, центрированы (имеют нулевое математическое ожидание) . То есть отсутствует систематическая ошибка

3. Они некоррелированы и имеют одинаковые конечные дисперсии

4. Случайная величина ε_i имеет нормальное распределение с параметрами 0, σ² .

Тогда оценки, полученные методом наименьших квадратов оказываются несмещенными, состоятельными, имеют наименьшую дисперсию среди линейных по y_i оценок.

Метод наименьших квадратов получил самое широкое распространение в практике статистических исследований в первую очередь благодаря двум главным своим преимуществам: во-первых, он не требует знания закона распределения обрабатываемых наблюдений, во-вторых, он достаточно хорошо разработан в плане вычислительной реализации.

Итак, в результате эксперименте мы получили набор значений (x₁,y₁), (x₂,y₂) ,… (x_n,y_n) . Наша задача найти регрессионную прямую, расстояние по оси OY от точек (x₁,y₁) до которой минимально. Для этого находят минимум функции _i ²=  (y_i – a ₁x_i – a₀)² , сумма берется по всем i от 1 до n. После дифференцирования и проведения преобразований получаем, что минимум этой функции равен min  ε_i ²= min  (y_i – a ₁x_i + a₀)² = (y_i – â ₁x_i –â₀)² ,

Он достигается при таких оценках параметров:

( )

, ( )

Суммирование ведется по всем индексам i от 1 до n включительно.

Таким образом, для нахождения коэффициентов линейной регрессии необходимо вычислить выборочные средние, суммы квадратов значений, суммы квадратов отклонений от среднего, суммы произведений значений переменных, суммы произведений значений одной переменной на отклонение от среднего другой.

Пример.

Вычислим уравнение регрессии методом наименьших квадратов. Для этого составим расчетную таблицу (по tasks.ru):

i	x	y	x2	y2	xy
1	3.92	8.06	15.3664	64.9636	31.5952
2	2.15	6.36	4.6225	40.4496	13.674
3	7.12	8.08	50.6944	65.2864	57.5296
4	9.39	8.75	88.1721	76.5625	82.1625
5	8.64	8.9	74.6496	79.21	76.896
6	11.2	12.39	125.44	153.5121	138.768
7	3.77	1.17	14.2129	1.3689	4.4109
8	3.56	3.35	12.6736	11.2225	11.926
9	2.2	2.44	4.84	5.9536	5.368
10	-2.81	0.38	7.8961	0.1444	-1.0678
11	4.63	7.41	21.4369	54.9081	34.3083
12	1.93	0.23	3.7249	0.0529	0.4439
13	3.25	4.29	10.5625	18.4041	13.9425
14	-1.61	-0.26	2.5921	0.0676	0.4186
15	1.46	2.66	2.1316	7.0756	3.8836
16	1.45	2.79	2.1025	7.7841	4.0455
17	-2.86	-0.64	8.1796	0.4096	1.8304
18	-0.08	1.36	0.0064	1.8496	-0.1088
19	-4.01	-2.84	16.0801	8.0656	11.3884
20	3.13	2.9	9.7969	8.41	9.077
21	1.25	3.17	1.5625	10.0489	3.9625
22	4.66	3.24	21.7156	10.4976	15.0984
23	6.06	6.78	36.7236	45.9684	41.0868
24	4.89	8.44	23.9121	71.2336	41.2716
25	5.13	5.2	26.3169	27.04	26.676
Сумма	78.42	104.61	585.4118	770.4894	628.5872

Таким образом, искомые коэффициенты: a₀ = 1,408, a₁ = 0,885

Уравнение регрессии: y=0,885x+1,408

В заключении укажем несколько обстоятельств, которые могут влиять на выводы при применении регрессионного анализа (можно сравнить с аналогичным пунктом темы 2.4).

1. Неоднородность данных, выбросы

2.Неадекватность модели

3. Скрытый фактор (третья переменная)