§21 «Доверительные интервалы» а.Н.Бородин «Элементарный курс теории вероятностей и мат.Статистики»

Напоминание. Оценка (Х₁… ,Х_n ) называется асимптотически нормальной с дисперсией Δ², если

(– ) сходится при n →∞ по распределению к стандартному нормальному закону (нормальное распределение при нулевом математическом ожидании и дисперсии, равной 1)

Асимптотически нормальными являются выборочное среднее, дисперсия, моменты

Замечание. Построение доверительного интервала основано на важнейшем свойстве функции распределения: вероятность того, что случайная величина примет значение из промежутка (х₁;х₂)равна приращению функции распределения на этом промежутке. P(x₁ Х < x₂) =F(x₂) –F(x₁)

Кроме того напомним, что F_Х (α) =P(Х < α).В частности, если некоторая величина имеет стандартное нормальное распределение с функцией распределения N(x), P(x₁ Х < x₂) =N(x₂) –N(x₁) иN_Х (α) =P(Х < α), где

, а - функция Лапласа

§21 «Доверительные интервалы» а.Н.Бородин «Элементарный курс теории вероятностей и математической статистики»

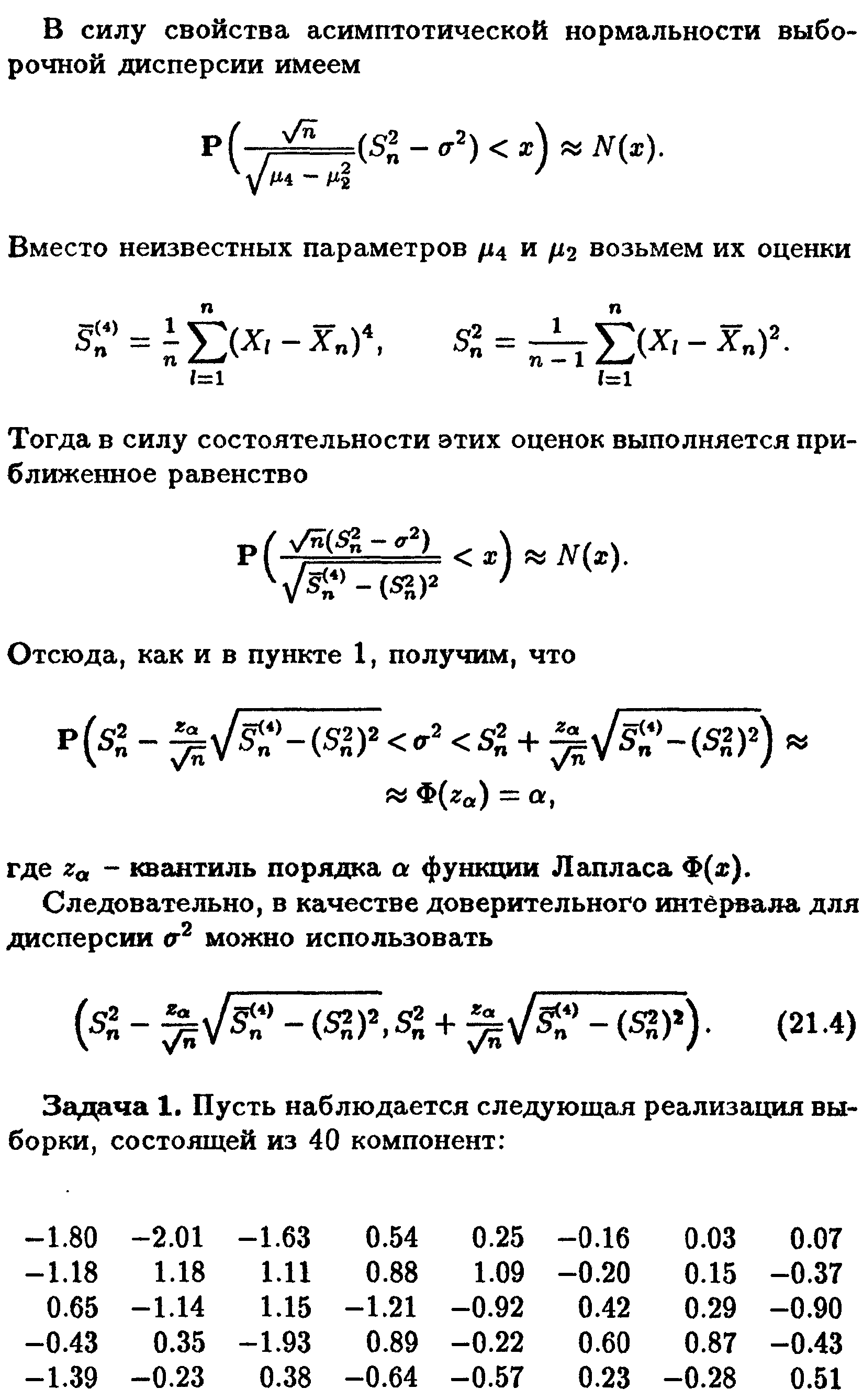
В случае, если рассматривается выборка из нормального закона, для построения доверительных интервалов используется Лемма (Теорема) Фишера:

Пусть Х₁, Х₂,…..Х_n  — независимая выборка из генеральной совокупности с нормальным законом распределения. Пусть — выборочное среднее, а— несмещённая выборочная дисперсия. Тогда

1. инезависимы

Замечание. Часто приходится слышать, что «независимые величины – это величины, не имеющие ничего общего». Это убедительный контрпример для подобного заблуждения: выборочное среднее и дисперсия не просто «имеют что-то общее», а вторая выражается через первое.

2. имеет стандартное нормальное распределение.Позволяет оценить неизвестное математическое ожидание при известной дисперсии и наоборот, неизвестную дисперсию по известному математическому ожиданию.

3. то есть имеет распределение «хи-квадрат» с n-1 степенью свободы. Позволяет оценить неизвестную дисперсию

4. ~t_n-1 , то есть имеет распределение Стьюдента с n-1 степенью свободы. Позволяет оценить неизвестное математическое ожидание.