
Image_slides / part4_pca
.pdf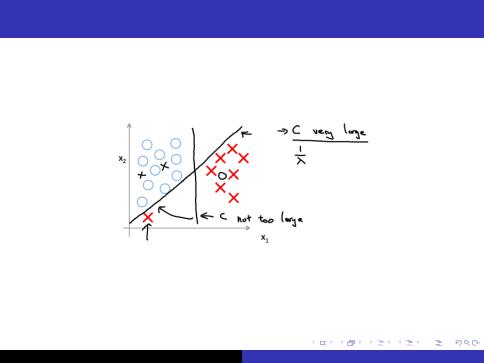
Meaning of C
Support Vector Machine
Lagrangian for Soft Margin
The Lagrangian
1 |
m |
m |
m |
|
X |
Xi |
X |
||
L(w; b; ; ; r) = |
|
w wT i (yi (w xi b) 1+ i )+C |
|
i ri i |
2 |
=1 |
|||
|
|
i=1 |
i=1 |
|
After setting the derrivatives with respect to w and b to zero and substituting them back we get
^ |
m |
1 |
m m |
|
i |
X |
|
|
XX |
L( ) = |
=1 |
i |
2 |
i j yi yj hxi ; xj i |
|
|
|
i=1 j=1 |
|
0 i C
m
X
i y(i) = 0
i=1
Support Vector Machine
Coordinate Ascent
Let we would like to solve uncostrained optimization problem
^
max L( 1; :::; m)
I Loop until convergence f
I for i = 1; ::; m
i :=
f |
|
|
^ |
^ |
; :::; m) |
argmax ^i L( 1 |
; :::; i 1; i ; i+1 |
I g
I g
Support Vector Machine
Sequential Minimal Optimization
^ |
m |
1 |
m m |
|
i |
X |
|
|
XX |
L( ) = |
|
i |
|
i j yi yj hxi ; xj i |
|
=1 |
|
|
i=1 j=1 |
0 i C
m
X
i y(i) = 0
i=1
IRepeat till convergence f
1.Select some pair i and j to update next (using a heuristic that tries to pick the two that will allow us to make the biggest progress towards the global maximum).
2.Reoptimize L( ) with respect to i and j , while holding all the other k (k 6= i; j) xed.
Ig
Support Vector Machine
References
Ien.wikipedia.org
Iwww.coursera.org Andrew Ng Machine Learning Course
IAndrew Ng Machine Learning Course cs229 http://cs229.stanford.edu/notes/cs229-notes3.pdf
Ihttp://www.machinelearning.ru
Ihttp://logic.pdmi.ras.ru/ yura/internet/07ia.pdf
Support Vector Machine
