
Image_slides / part4_pca
.pdf
Dimensionality Reduction
December 7, 2012
1/36
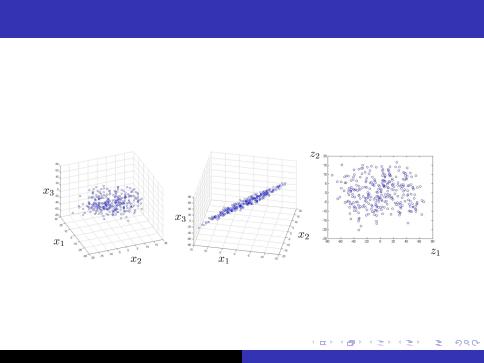
Objective
Reduce data from 3D to 2D
2/36
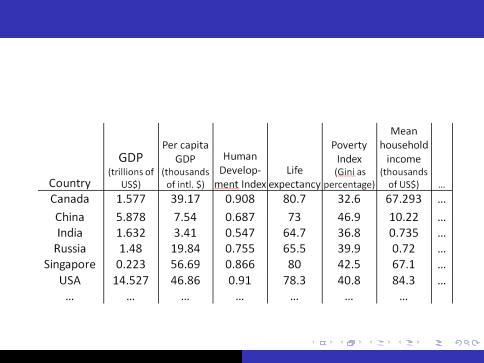
Motivating Example
3/36
Motivating Example
4/36
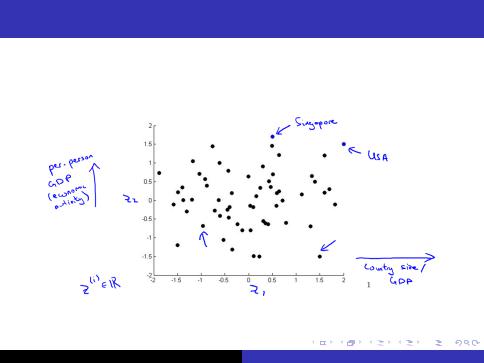
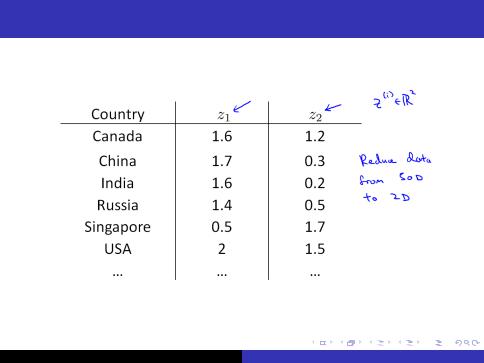
Motivating Example
5/36
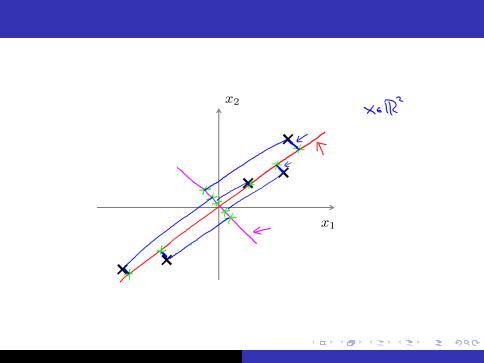
Principal Component Analysis (PCA) problem formulation
6/36
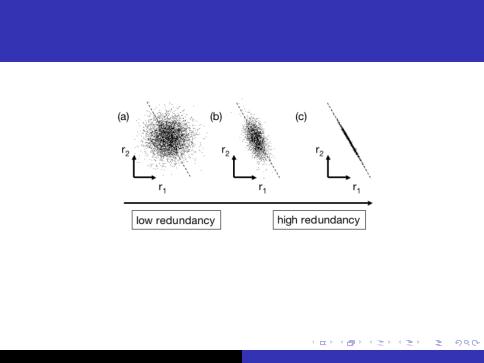
Principal Component Analysis (PCA) statistical problem formulation
1;1 |
0 |
|
I Covariation matrix for (a) 0 |
2;2 |
|
1;1 |
1;2 |
|
I Covariation matrix for (c) 2;1 |
2;2 |
7/36

Covariance
01
|
|
j |
|
|
j |
|
j |
|
X = x1 x2 |
|
xn |
|
|||||
|
|
j |
|
|
j |
|
j |
|
Let each x |
|
|
|
mean |
||||
@ |
1 |
|
i |
has zero |
|
A |
||
i;j = |
|
xiT xj |
|
|
|
|||
n 1 |
|
|
|
|||||
|
|
|
|
|
|
|
||
Ii = j - variance
Ii <> j - covariance
Iif i;j = 0 then xi and xj tottaly uncorrelated
SX = n 1 1 X T X - covariance matrix
8/36
Change of Basis
ILet P be the n n matrix. And each row is basis vector of new subspace
PX = |
0 |
p2 |
1 |
|
xj1 xj2 |
|
xjm |
|
|
|
|
p1 |
|
0 j |
|
|
|
1 |
|
|
B |
|
C |
j |
|
j |
|||
|
B |
pn |
C@ |
|
|
A |
|||
|
@ |
|
A |
|
|
|
|
|
|
where each jjpi jj = 1
IEach product pi xj - is the length of progection of each xj onto vector pi
IIn other words each product pi xj is the coordinate on axis pi
9/36
Desired Covariance Properties
IWe would like to nd matrix P such that the covariances between transformed feature vectors to be zero.
Sy = n 1 1Y T Y , where Y = PX
IIn this case we eliminate all redundancy.
IThe rows of matrix P are the principal components
10/36
