2. Для сравнения выборочных средних и дисперсий также можно воспользоваться приложением «Анализ данных» в Microsoft Excel.

А. Сравнение выборочных дисперсий.

Выбираем раздел меню Данные - «Анализ данных»-«Двухвыборочный тест для дисперсии» (Рис. 8).

Рис. 8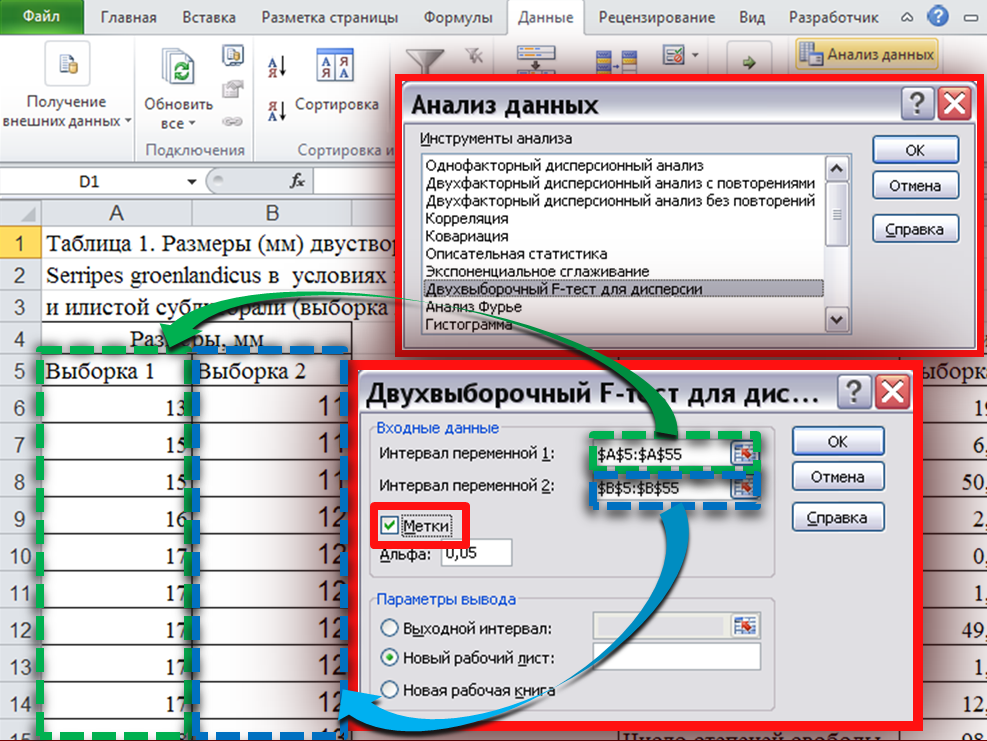

В появившимся окне указываем диапазоны ячеек с вариантами обеих выборок («Интервал переменной 1» и «Интервал переменной 2), если диапазон ячеек выделяем вместе с названием столбцов ставим отметку в окошке «Метки», нажимаем «ОК» (как показано на Рисунке 8) и получаем таблицу с результатами.

Б. Сравнение средних.

Выбираем раздел меню «Данные»-«Анализ данных»-«Двухвыборочный t-тест с одинаковыми дисперсиями» (Рис. 9).

В

Рис. 9.

появившимся окнеуказываем диапазоны ячеек с вариантами обеих выборок («Интервал переменной 1» и «Интервал переменной 2). Если диапазон ячеек выделяем вместе с названием столбцов, ставим отметку в окошке «Метки», нажимаем «ОК» (как показано на Рисунке 9) и получаем таблицу с результатами.

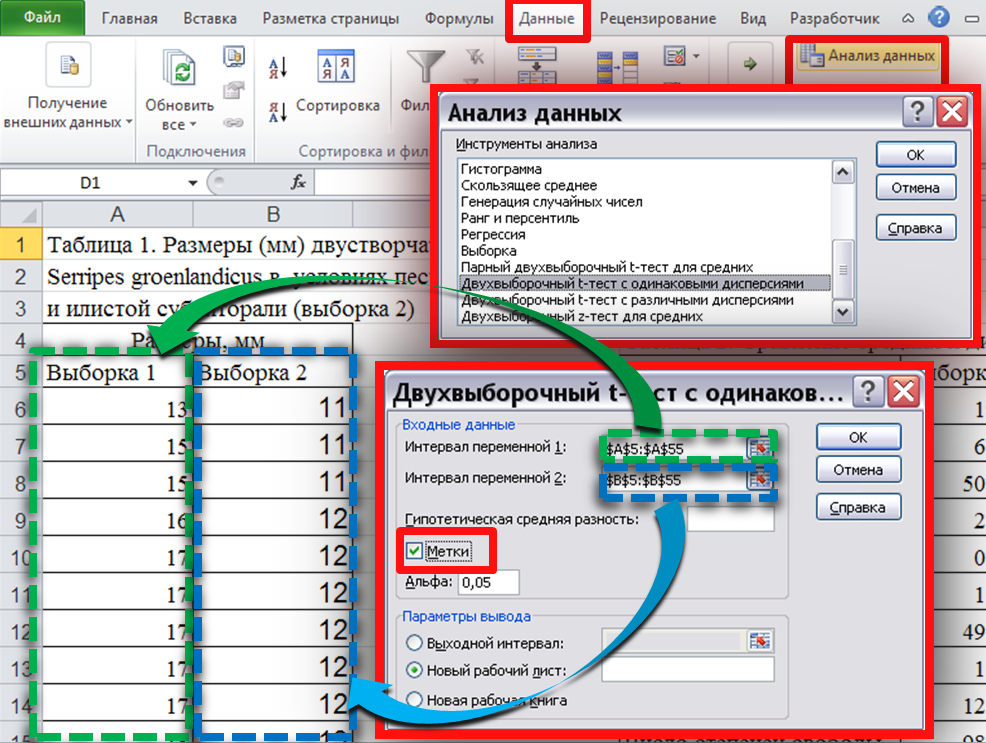
3. Сравнение двух выборок с помощью приложения «Статистика».

Для начала подготовим наши данные: сгруппируем данные обеих выборок в единый ряд и введем еще одну переменную - код выборки: значениям признака из выборки 1 соответствует 1, значениям признака из выборки 2 – соответствует цифра 2 (Таблица 3).

Таблица 3. Исходные данные

Варианты

Код выборки

Вставляем данные (оба столбца) в специальную таблицу Spreadsheet. Выбираем последовательно разделы Statistics-Basic Statistics/Tables-t-test, idependent by groups (как показано на Рисунке 10).

Рис. 10-11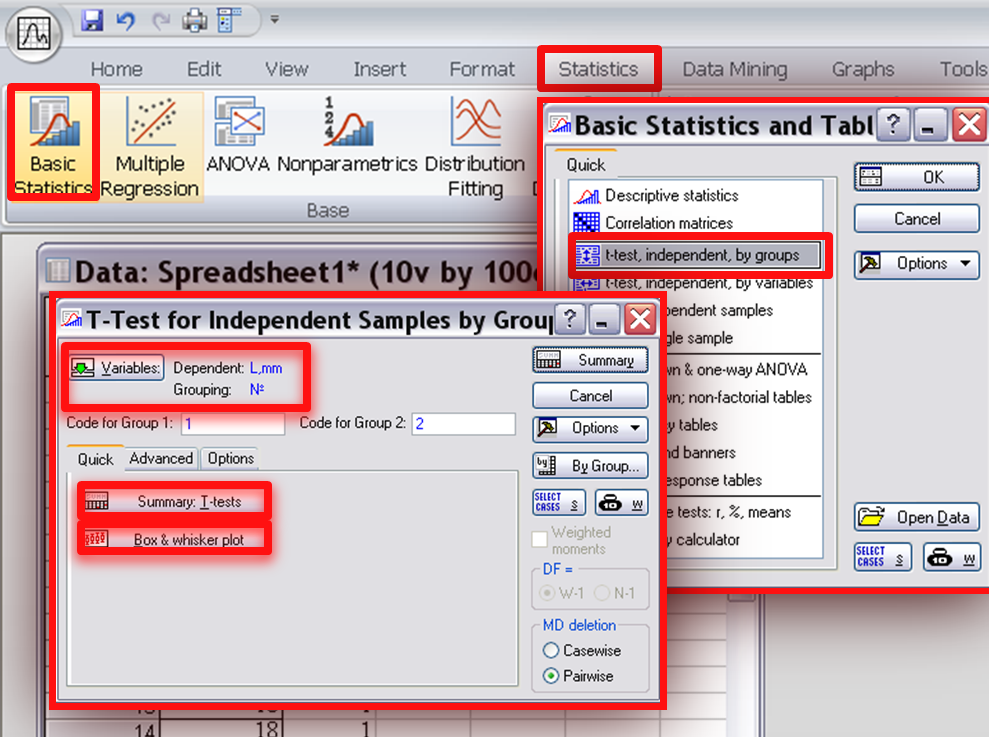

В открывшейся вкладке (Рис. 11) нажимаем кнопку Variables, чтобы указать, в каком столбце находятся значения изучаемого признака (Dependent variables), в каком - значения группирующей переменной (Grouping variables), в данном случае это коды выборки.

Нажимая кнопки Summary: T-tests и Box&whisker plot соответственно получим таблицу с итогами сравнения выборок и графическое изображение средних значений в выборках с различными видами интервалов.

Для более точного графического изображения доверительного интервала для средних обеих выборок следует воспользоваться разделом меню Graphs-Means w/Error Plots….(Рис. 12). В появившемся окне нажимаем кнопку Variables и указываем, в каком столбце находятся данные: Dependent variable (значения признака) и Grouping variable (коды выборки). Все остальные отметки оставляем неизменными (тип графика Graph type– Whiskers; группировка данных в б/интервальный вариационный ряд – Grouping intervals - Unique value, тип интервала – 95% доверительный интервал - Whiskers - Conf. Interval) и нажимаем ОК.

Рис. 12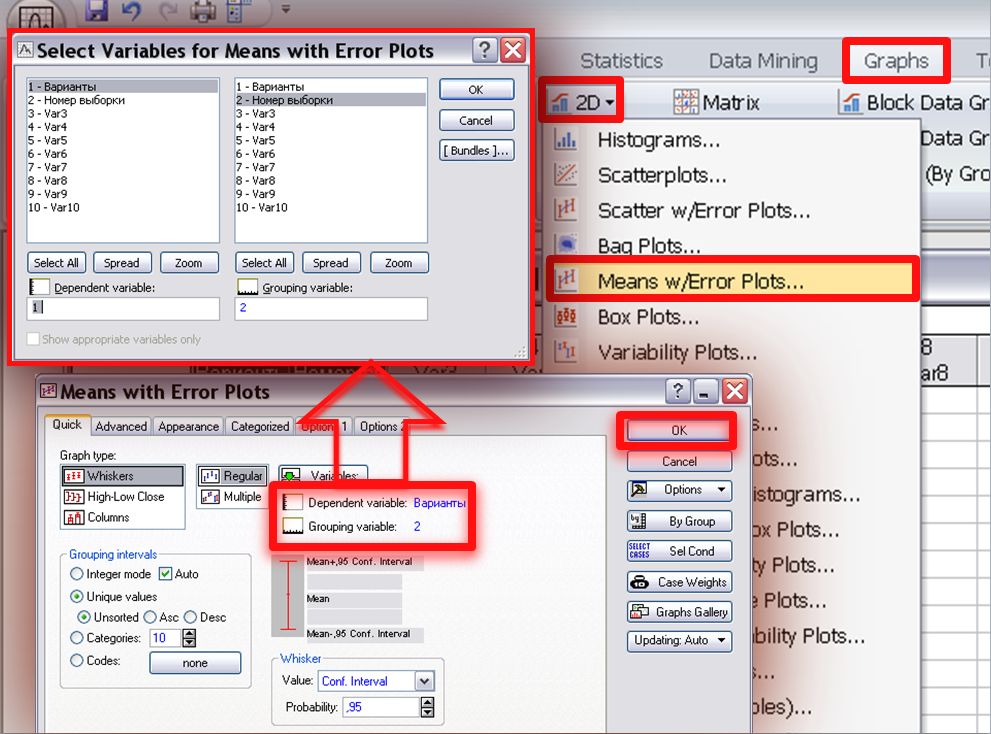

4. Непараметрическое сравнение выборочных статистик.

U-критерий Манна-Уитни Ограничения применимости критерия

1. В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти.

2. В каждой выборке должно быть не более 60 значений параметра, но уже при выборках в 20 и более единиц ранжирование становится довольно трудоемким.

Для применения U-критерия Манна-Уитни нужно произвести следующие операции.

1. Составить единый ранжированный (в порядке возрастания) ряд из обоих сопоставляемых выборок, каждому значению признака присвоить ранг (ранги –числа натурального ранга; меньшему значению присваивается меньший ранг; одинаковым значениям признака присваивается одинаковый средний ранг).

2. Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм (T_x), соответствующую выборке с n_x единиц.

3. Определить значение U-критерия Манна-Уитни по формуле: .

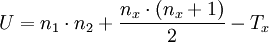4. По таблице определить критические значения критерия для данных n₁ и n₂. Если полученное значение U меньше табличного или равно ему для избранного уровня статистической значимости, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.

Задача.

Но: Наблюдаемые различия между значениями признака в рассматриваемых выборках случайны.

На: Наблюдаемые различия между значениями признака в рассматриваемых выборках не случайны.

А. Ранжируем варианты обеих выборок в один общий ряд. Для этого:

1. Создадим еще одну таблицу (Табл. 4): 1 столбец – значения признака (в обеих выборках), 2 столбец – номер выборки.

2. В

   Рис. 13

   ыделяем оба столбца (без названий) и сортируем (Данные-Сортировка) данные по столбцу со значениями признака (Рис. 13).

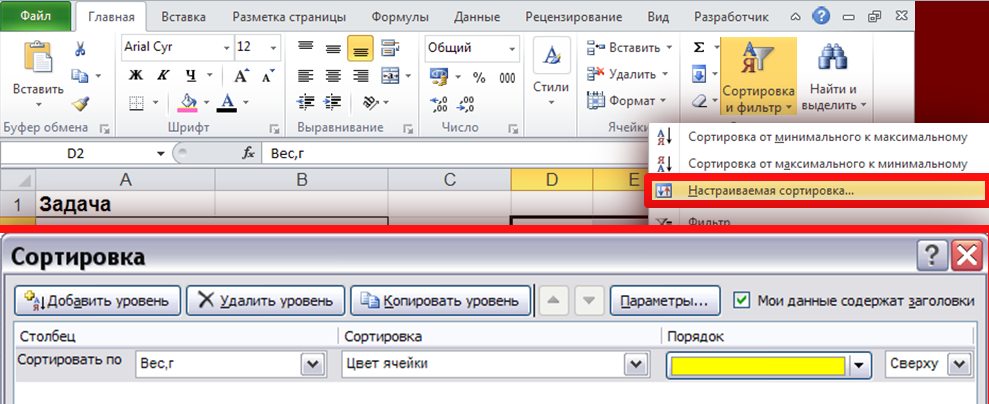
3. Вводим еще два столбца: 1- с порядковыми значениями вариант и 2 – где вычисляем для каждой варианты ранг (одинаковым значениям признака присваивается одинаковый ранг) (Табл. 4).

Табл. 4. Ранжирование данных обеих выборок в единый ряд и присвоение рангов отдельным значениям признака.

Варианты	Номер выборки	Порядковый номер	Ранги

Находим сумму рангов отдельно для каждой выборки (можно опять воспользоваться сортировкой данных – выделить всю таблицу и отсортировать по столбцу Номер выборки), результаты оформляем в виде таблицы - Табл. 5.

Таблица 5. Сравнение выборок с помощью критерия Манна-Уитни

Показатели	Выборка 1	Выборка 2
Сумма рангов
Объем выборки
Критерий Манна-Уитни (U)
Ust

Примечание: N₁ и N₂ – ранги вариант первой и второй выборки

Но принимается если U>Ust.

U_st берем из таблицы (файл табл.кр. знач.Манна_Уитни.pdf).