
hitrov-1st-semester / Paragraf_12
.pdf
§12. Комплексные числа. Обоснование и интерпретация.
1.Обоснование комплексных чисел.
Обращаясь к комплексным числам, приведем краткий исторический материал, заимствовав его, как и многое другое, из учебника Д.К. Фаддеева «Лекции по алгебре».
«Как известно, комплексными числами называются выражения вида a bi , где a и
b – вещественные числа, i – некоторый символ, удовлетворяющий соотношению i2 1. Первые попытки введения в математику комплексных чисел были сделаны итальянскими математиками 16 в. Кардано и Бомбелли в связи с решениями уравнений третьей и четвертой степеней. Однако признание комплексных чисел как ценного орудия исследования происходило очень медленно. Недоверие вызывал сам символ i («мнимая единица»), заведомо не существующий среди вещественных чисел. Это недоверие усугублялось тем, что некритическое перенесение некоторых формул обычной алгебры на
комплексные числа порождало неприятные парадоксы (например, i2 1, но вместе с
тем, используя формальное выражение |
i |
1 |
|
и |
обычные правила действий с |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратными |
корнями, |
получим |
1 i2 |
1 |
1 |
( 1)2 1 1 |
(наше |
||||||||
видоизменение формулы – Г.Х.)). Лишь в 19 в. Гауссу удалось дать достаточно убедительное обоснование понятия комплексного числа. Построенная в 19 в. на основе комплексных чисел теория функций комплексного переменного обогатила математический анализ новыми результатами, придала значительной части математического анализа чрезвычайную стройность и чистоту, а в дальнейшем оказалась могущественным средством исследования в важных разделах механики и физики. Таким образом, «невозможные», «мнимые» числа явились ценнейшим средством исследования, и тем самым их введение в науку оказалось оправданным не только их непротиворечивостью, но и практической важностью».
Поскольку любое комплексное число в записи a bi |
определяется парой |
вещественных чисел a и b, то в указанном учебнике для введения |
комплексных чисел |
рассматриваются упорядоченные пары (a,b) вещественных чисел, на множестве которых специальным образом заданы операции сложения и умножения. Показывается, что, относительно введенных операций сложения и умножения упорядоченные пары образуют структуру поля, т.е. упорядоченные пары можно складывать, вычитать, умножать, делить, возводить в степень и.т.д. Кроме того, появляется дополнительная операция – умножение упорядоченных пар на вещественные числа, по тому же правилу, как мы умножали матрицы на числа (по сути, упорядоченная пара и есть частный случай матрицы). В учебнике показывается, что в множестве пар, существует пара (0,1), произведение которой на себя (квадрат пары) дает пару (-1,0), а произведение пары (b,0) на пару (0,1) дает пару (0,b). Поскольку сложение пар задается так же как сложение матриц (сложить пары означает сложить соответствующие элементы), то пару (a,b) можно представить в виде:
(a,b) (a, 0) (0,b) (a, 0) (b, 0) (0,1) .
Далее, поскольку пары |
вида (a, 0) |
замкнуты относительно операций сложения |
( (a, 0) (b, 0) (a b, 0) ), |
умножения пар |
( (a, 0) (b, 0) (ab, 0) ), умножения этих пар на |
вещественные числа ( (a, 0)b b(a, 0) (ab, 0) ), то предлагается отождествить пары такого вида с вещественными числами. То есть, предлагается положить (a, 0) a . Теперь, если для пары (0,1) ввести специальное обозначение i , получим:
(a,b) (a, 0) (0,b) (a, 0) (b, 0) (0,1) a bi
(последний знак равенства означает эквивалентность предыдущей записи с последней). При этом, согласно принятым договорѐнностям, имеем
i2 1
Такой подход к введению комплексных чисел позволяет лишить «мнимую» единицу еѐ таинственного мистического смысла, поскольку i (0,1) , т.е. лишь обозначение вполне
реальной пары вещественных чисел. С другой стороны, договоренности относительно отождествления пар вида (a, 0) с вещественными числами и относительно обозначения
i (0,1) позволяют вернуться к привычным (со школы) обозначениям комплексных чисел
и не впадать в затруднение, приведенное в цитате.
Выше мы не стали приводить определение умножения пар, не стали останавливаться на некоторых трудностях доказательств аксиом поля для пар, но, по сути, изложили схему введения комплексных чисел. Тем самым мы как бы заявили, что будем вводить комплексные числа иначе. Сразу же успокоим читателя, что никаких особых новшеств по сравнению с упомянутым выше учебником не будет. Мы просто будем использовать замечание учебника, что комплексные числа являются конкретным примером не оговоренной пока алгебраической структуры, которая носит такое же название как изучаемый нами раздел математики, т.е. алгебра.
Поясняющее определение. В различных разделах математики возникает потребность рассматривать векторные пространства (смотри Определение 5 параграфа 3) над данным полем P, в которых кроме действий сложения и умножения на числа поля определено ещѐ действие умножения, сопоставляющее каждой паре «векторов» (элементов векторного пространства) третий вектор того же пространства – их «произведение». В этой ситуации всегда естественно предполагать, что результат умножения векторов X и Y, т.е. XY, линеен по каждому из сомножителей при фиксированном втором:
(c1 X1 c2 X2 )Y c1 X1Y c2 X2Y и X (c1Y1 c2Y2 ) c1XY1 c2 XY2 .
Пространство с умножением, удовлетворяющим такому требованию билинейности, называется алгеброй над полем P.
Иначе можно сказать, что алгебра есть кольцо и линейное (векторное) пространство с естественным согласованием «кольцевого» умножения и векторных (линейных) действий. Именно сложение в кольце и сложение в векторном пространстве совпадают, а свойства дистрибутивности для умножения «усиливаются» до линейности по каждому множителю, для чего достаточно потребовать, чтобы (cX )Y X (cY ) cXY при
любых c P и X и Y из алгебры.
Несмотря на относительную новизну и некоторую абстрактность введенного определения новой структуры – алгебры, мы с ней уже сталкивались, когда рассматривали множество квадратных матриц порядка n, т.е. M n . Действительно. То, что M n является
линейным пространством над полем P, которому принадлежат элементы матриц, мы уже показывали в параграфе 3. Более того, в пункте 6 названного параграфа мы отмечали, что M n является ассоциативным кольцом с единицей. Тем самым мы ещѐ в параграфе 3
показали, что M n является алгеброй, хотя и не использовали этого термина. Более того, в
упражнении, которым заканчивается параграф 3, мы, опять таки не вводя термина, фактически ввели комплексные числа.
Напомним, в этом упражнении требовалось показать, что множество квадратных
матриц вида |
a |
b |
с вещественными элементами, относительно операций |
A |
|
||
|
b |
a |
|
сложения и умножения матриц образует структуру поля. Вернемся к этому упражнению.
Обозначим |
через |
C множество |
матриц вида |
|
a |
|
b |
с вещественными |
|||||
A |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
b |
|
|
a |
|
|
элементами. Очевидно, что C M2 |
и |
|
|
|
|
|
|
|
|
||||
a |
b |
1 |
0 |
0 |
1 |
|
1 |
0 |
|
0 |
1 |
||
A |
|
a |
|
b |
|
aE bI , где |
E |
|
|
|
и |
I |
. |
b |
a |
0 |
1 |
1 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |

То есть, множество C есть множество линейных комбинаций матриц E и I с вещественными коэффициентами. Воспользуемся полученными знаниями о линейной зависимости и независимости строк (столбцов), применив их к нашим матрицам E и I, и покажем, что эти матрицы линейно независимы. Приравняем для этого линейную комбинацию x1E x2 I нулевой матрице, т.е. рассмотрим выражение x1E x2 I 0 . Так как
ненулевые элементы матрицы E расположены там, где расположены нули матрицы I, и, наоборот, ненулевые элементы матрицы I расположены там, где расположены нули матрицы E, то x1E x2 I 0 возможно тогда и только тогда, когда x1 x2 0 . Значит,
матрицы E и I действительно линейно независимы и составляют базисную совокупность в множестве матриц C.
Поскольку, изучая множество C, нам придется действовать с линейными комбинациями матриц E и I, то выпишем значения различных попарных произведений этих матриц:
EE E2 E , EI IE I , I I I 2 E . |
(*) |
При изучении матриц мы рассматривали операцию транспонирования матриц, т.е. |
|
операцию, сопоставляющую матрице A матрицу AT . Для матрицы |
I C имеем: I T I . |
Поэтому, если матрица A C и A aE bI , то AT aE bI C. В этом случае матрицу AT будем также обозначать через A и называть сопряженной к A. Таким образом, если
A aE bI , то A aE bI .
Подчеркнем замечательное свойство сопряженных матриц:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 )E (det A)E |
|
A |
A |
2aE и AA |
AA (a2 |
|||||||||||||||
Для A1, A2 C из свойств транспонирования матриц следует также, что |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A1 A2 |
A1 A2 и A1 A2 A2 A1 . |
(**) |
||||||||||||||||
Покажем, что множество матриц C относительно операций матричного сложения и матричного умножения образуют кольцо и изучим свойства этого кольца. Начнем с того, что нам нужно показать замкнутость операций сложения и умножения матриц. Пусть
A1, A2 C. Отсюда |
следует, что |
A1 a1E b1I , |
A2 a2 E b2 I , где a1, a2 ,b1,b2 |
R |
|
(вещественные |
числа). |
Тогда |
A1 A2 (a1 a2 )E (b1 b2 )I C |
и |
|
A1 A2 (a1E b1I)(a2 E b2 I) a1a2 E b1a2 I a1b2 I b1b2 E (a1a2 b1b2) E (a1b2 b1a2) I C
(обращаем внимание, что при доказательстве замкнутости произведения матриц из C мы пользовались как свойствами умножения матриц на числа, так и формулами (*)).
Выпишем теперь свойства сложения и умножения матриц из C.
1.(A1 A2 ) A3 A1 (A2 A3 ) (вытекает из ассоциативности сложения матриц).
2.0 C (нулевая матрица) такая, что A 0 A для любой A C (очевидно).
3.Для любой A C существует матрица (-A), такая что A ( A) 0 (очевидное
свойство существования в C для любой матрицы противоположной ей матрицы).
4.A1 A2 A2 A1 (очевидно).
5.(A1 A2 )A3 A1 (A2 A3 ) (вытекает из ассоциативности умножения матриц).
6.В C существует единичная матрица E, такая что AE A для любой A C .
7. Для любой A 0 , A C, в C существует обратная к A матрица A 1 , такая что
AA 1 E .
Действительно. Положим |
a |
b |
, причем из A 0 |
следует, что или |
A aE bI |
|
|||
|
b |
a |
|
|
a 0 , или (и) b 0 . Но тогда det A a2 b2 0 . |
Следовательно, для ненулевой матрицы |
|||
A существует обратная |
A 1 |
|
|
1 |
|
|
|
a |
b |
|
|
|
a |
|
E |
|
|
b |
|
I , которая, |
очевидно, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
||||||||||||
|
|
|
a |
|
b |
|
|
b |
a |
|
a |
|
b |
|
|
a |
|
b |
|
|
|
|||
принадлежит C. Обратную матрицу к ненулевой матрице A можно также записать в виде |
||||||||||||||||||||||||
|
|
A 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
det A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. A1 A2 A2 A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
пусть |
|
|
|
|
|
|
|
|
A1 a1E b1I , |
|
|
|
A2 a2 E b2 I . |
Тогда |
|||||||||
A1 A2 (a1E b1I )(a2 E b2 I ) (a1a2 b1b2 )E (a1b2 b1a2 )I и |
|
|
|
|||||||||||||||||||||
A2 A1 (a2 E b2 I )(a1E b1I ) (a2a1 b2b1 )E (a2b1 b2a1 )I . |
|
|
|
|||||||||||||||||||||
Поскольку |
a1, a2 ,b1,b2 R, |
то с учетом свойств вещественных чисел, и получаем, что |
||||||||||||||||||||||
A1 A2 A2 A1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
(A1 A2 ) A3 A1 A3 A2 A3 |
|
(следует |
из |
|
замкнутости |
операций сложения и |
|||||||||||||||||
умножения для матриц в C и из свойства дистрибутивности умножения для матриц). |
||||||||||||||||||||||||
Рассматривая полученные свойства операций сложения и умножения матриц из C, |
||||||||||||||||||||||||
мы видим, что C является полем относительно указанных операций. Кроме того, C |
||||||||||||||||||||||||
является векторным пространством над полем вещественных чисел. То есть C является |
||||||||||||||||||||||||
алгеброй над полем вещественных чисел. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Установим теперь взаимно однозначное соответствие между матрицами из C и |
||||||||||||||||||||||||
выражениями «вида a bi , где a |
и b – |
вещественные числа, i – некоторый символ, |
||||||||||||||||||||||
удовлетворяющий соотношению i2 1», |
положив (aE bI ) a bi . Это соответствие |
|||||||||||||||||||||||
обладает свойством:
(c1 (a1E b1I ) c2 (a2 E b2 I )) ((c1a1 c2a2 )E (c1b1 c2b2 )I )) c1a1 c2a2 (c1b1 c2b2 )i
c1 (a1 b1i) c2 (a2 b2i) c1 (a1E b1I ) c2 (a2 E b2 I ),
которое называется свойством линейности – линейная комбинация прообразов отображается в линейную комбинацию образов с теми же коэффициентами. В этом случае также говорят, что - линейное отображение.
Кроме того,
((a1E b1I )(a2 E b2 I )) ((a1a2 b1b2 )E (a1b2 b1a2 )I ) (a1a2 b1b2 ) (a1b2 b1a2 )i
(a1 b1i)(a2 b2i) (a1E b1I ) (a2 E b2 I ).
Второе свойство показывает, что преобразует произведение прообразов в произведение
образов.
Взаимнооднозначное отображение, обладающее двумя указанными свойствами,
называется изоморфизмом алгебр.
В силу установленного изоморфизма между матрицами aE bI и выражениями
вида a bi , где a и b – вещественные числа, мы видим, что выражения |
вида |
a bi |
с |
обычными операциями почленного сложения и умножения с учетом, |
что |
i2 1, |
|
образуют структуру поля. Это поле мы и будем называть полем комплексных |
чисел, |
а |
|
элементы этого поля, соответственно, комплексными числами. Обозначать его будем, как и алгебру, буквой C. Впредь, чтобы не произошло путаницы, там, где речь будет идти об алгебре C, мы так и будем писать – алгебра C.
В комплексном числе z a bi , числа a и b называются его компонентами. Первая компонента называется вещественной частью числа z и обозначается Re z , а вторая компонента называется его мнимой частью и обозначается Im z . Подчеркнем, что мнимая часть (так же, как и вещественная часть) комплексного числа есть число вещественное.
Пока мы не покинули алгебру C и окончательно не перешли к полю C, отметим,
как переносятся свойства сопряженности из алгебры в поле. Пусть |
A aE bI и пусть |
||
|
|
||
z a bi . Тогда ( A) z и, следовательно, ( |
A |
) z a bi . Число |
z a bi называется |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
комплексно сопряженным к числу z. Из |
|
A |
A |
2aE |
следует, |
что |
|
|
z z 2a ; |
|
|
из |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
AA |
(a2 b2 )E , что z z a2 b2 ; из A A |
A A , что |
|
z z |
2 |
z z |
2 |
; |
из |
|
A A A A |
|||||||||||||||||||||||
1 |
2 |
1 |
2 |
|
|
1 |
|
1 |
|
|
1 |
2 |
|
|
|
|
1 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z |
|
|
из A 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
(учтена коммутативность умножения матриц из C), что z z |
2 |
2 |
; |
|
|
A , |
что |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
det A |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z 1 z1z z .
Итак, мы начали наше знакомство с комплексными числами (смотри цитату) с того, что определили их как выражения вида a bi и закончили тем же самым. Было ли это движение по кругу? Пусть читатель ответит себе на этот вопрос сам. Мы же перейдем к дальнейшему изучению свойств комплексных чисел, сделав предварительно одно
Замечание. В прикладной математике математика используется как инструмент для решения практических задач методами математического моделирования. Поэтому в прикладной математике, как правило, используются конкретные представители структур. Так говоря о множестве комплексных чисел, мы могли и не сообщать, что это множество является алгеброй. То же самое можно сказать об известном уже множестве квадратных матриц и неизвестных пока многочленах и кватернионах – это все примеры алгебр. Что же дает нам акцентирование на названиях структур? Оно, с одной стороны, позволяет подчеркнуть родство названных (и неназванных) разных математических объектов. С другой стороны, подчеркнуть, что кроме прикладных математиков, есть так называемые «чистые» математики, которые занимаются изучением алгебраических структур в «чистом виде», т.е. безотносительно к их конкретным представителям. Это знание полезно, поскольку позволяет связать конкретную построенную математическую модель с той или иной структурой и при нужде обратиться к тому или иному разделу математики или математикам (чистым). Сказанное относительно алгебр, имеет место и относительно других упоминавшихся алгебраических структур.
2. Вычитание и деление комплексных чисел.
В параграфе 2 мы уже отметили простейшие следствия определения поля. Повторим их здесь применительно к комплексным числам, ввиду важности последних для нашего раздела математики, и, заодно, ещѐ раз наведем мосты меду школьными знаниями действий вычитания и деления и излагаемыми здесь сведениями.
Действия вычитания и деления комплексных чисел определяются как действия, обратные к действиям сложения и умножения, т.е. вычитание – как действие, восстанавливающее одно из слагаемых по данной сумме и второму слагаемому, а деление
– как отыскание одного из сомножителей по данному произведению и второму сомножителю. Их возможность и единственность обосновывается следующими предложениями.
Пр. 1. Пусть z и w – данные комплексные числа. Тогда существует одно и только одно комплексное число x такое, что z x w, именно, x ( z) w . (напомним, (-z) -
противоположный по отношению к z элемент поля C). |
|
|
Доказательство. Имеем, z (( z) w) z ( z) w w , так что |
x ( z) w |
|
удовлетворяет поставленному требованию. |
Обратно, если z x w верное равенство, то |
|
( z) z x ( z) w , откуда x ( z) w , |
так что всякое число, отличное от |
( z) w не |
удовлетворяет поставленному требованию. Число ( z) w есть, таким образом, разность
чисел w и z. Она обозначается обычным образом: w z .
Пр. 2. Пусть z и w – данные комплексные числа, причем z 0 . Тогда существует одно и только одно комплексное число x такое, что zx w , именно, x z 1w . (напомним, z 1 - обратный по отношению к ненулевому z элемент поля C).
Доказательство. Если |
x z 1w , то |
zx z(z 1w) zz 1w w , |
т.е. |
x удовлетворяет |
||||||||||||||||||
требованию. Если zx w - верное равенство, |
то |
z 1 (zx) z 1w , откуда |
x z 1w , |
что и |
||||||||||||||||||
требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Число z 1w есть, таким образом, частное от деления w на z. |
Частное обычно |
|||||||||||||||||||||
записывается в форме дроби |
w |
. Ясно, что если zx w , то при любом t C, t 0 будет |
||||||||||||||||||||
z |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tzx tw , откуда |
x |
tw |
, таким образом, числитель и знаменатель дроби можно умножать |
|||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
tz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
на одно и то же число, отличное от нуля. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Удобно фактически вычислять частное |
w |
, |
умножая числитель и знаменатель, на |
|||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
||
число, сопряженное со знаменателем: |
|
w |
|
wz |
, |
так как zz |
есть вещественное число. |
|||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
zz |
|
|
|
|
|
|
|
|
|
||
Например, |
1 3i |
|
(1 3i)(1 i) |
|
2 4i |
1 2i . |
|
|
|
|
|
|
|
|||||||||
1 i |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(1 i)(1 i) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Конечно, |
этот способ |
равносилен, |
представлению |
числа |
z 1 |
в виде |
|
1 |
z , |
|||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zz |
||
указанному выше для z a bi .
3. Геометрическая интерпретация комплексных чисел в декартовых координатах.
Комплексное число z a bi естественно изобразить точкой на плоскости, приняв числа a и b за координаты точки, изображающей число z. При этом каждому комплексному числу соответствует точка и каждой точке плоскости соответствует некоторое комплексное число. Вещественные числа изображаются точками с равными нулю ординатами, т.е. точками, лежащими на оси абсцисс. На оси ординат располагаются изображения «чисто мнимых» чисел bi . Началу координат соответствует число 0.
Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексной переменной. Еѐ ось абсцисс называется вещественной осью, ось ординат –
мнимой осью в соответствии с наименованием чисел, изображения которых лежат на этих осях.
Наряду с изображением комплексных чисел точками на плоскости удобно с каждым комплексным числом связывать вектор, исходящий из начала координат в точку,
изображающую это |
число (т.е. |
радиус-вектор этой точки). |
Компоненты a и |
b |
комплексного числа |
z a bi |
являются, очевидно, проекциями |
(алгебраическими, |
с |
учетом знаков) этого вектора на оси координат. Как известно, проекция суммы векторов (в смысле векторного сложения) на любую ось равна сумме проекций слагаемых. Поэтому сумма векторов, изображающих комплексные числа z и w есть вектор, изображающий сумму z w этих чисел, так как компоненты числа z w равны суммам соответствующих компонент слагаемых (рис.1).
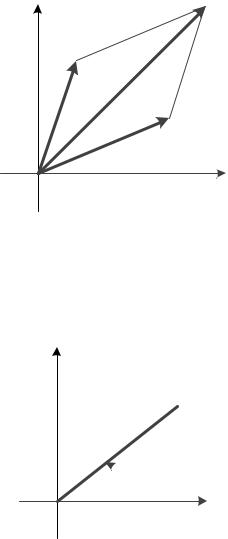
z+w |
w |
z |
Рис. 1.
4. Геометрическая интерпретация комплексных чисел в полярных координатах. Модуль и аргумент комплексного числа.
Введем в рассмотрение полярные координаты точки, изображающей комплексное число z, принимая начало координат за полюс и вещественную ось за полярную ось
(рис.2).
 z
z
r
 φ
φ
Рис. 2.
Как известно, полярными координатами точки являются длина еѐ радиус-вектора, равная расстоянию от точки до полюса, и величина еѐ полярного угла, образованного положительным направлением полярной оси и радиус-вектором рассматриваемой точки. Длина радиус вектора точки, изображающей комплексное число z, называется модулем этого числа и обознается |z|. Ясно, что | z | 0 , причем | z | 0 только, если z 0 . Величина
полярного угла точки, изображающей комплексное число z, называется аргументом этого числа и обозначается arg z . Заметим, что arg z имеет смысл лишь при z 0 , аргумент
числа 0 смысла не имеет.
Положительным направлением отсчета аргумента комплексного числа считается направление от положительной полуоси вещественной оси к положительной полуоси мнимой оси, т.е. против часовой стрелки при обычном расположении осей.
Аргумент комплексного числа определен не однозначно, так как угол между двумя направлениями (даже если выбрано положительное направление отсчета) можно отсчитывать многими способами. Уточним характер многозначности аргумента. Пусть 0
- наименьшее значение аргумента, отсчитанное в положительном направлении. Сделав при отсчете несколько полных оборотов в положительном направлении, мы придем к
значению аргумента 0 |
k 2 , где |
k – число полных оборотов, т.е. целое |
неотрицательное число. |
Простейший |
отсчет в отрицательном направлении дает |
(2 0 ) 0 2 (рис.3). |
|
|

 z
z
 φ0
φ0
φ0 – 2π
Рис. 3.
Если же сделать ещѐ s полных оборотов в отрицательном направлении, мы придем к значению 0 (s 1)2 , s 0 . Тем самым все возможные значения аргумента даются
формулой: 0 2k , где k любое целое число, положительное, отрицательное или 0.
Таким образом, данному комплексному числу, не равному 0, можно соотнести в качестве аргумента бесконечное множество чисел, правда, очень просто связанных между собой, именно, любые два значения аргумента отличаются на целое кратное 2 .
Разумеется, многозначности аргумента можно было бы избежать, наложив на аргумент какие-либо требования, выделяющие одно значение из всех возможных, например, 0 2 или . Однако это оказывается неудобным, особенно при изучении функций от комплексной переменной. Пусть, например, комплексное число x yi изменяется так, что его изображение описывает в положительном направлении
окружность с центром в начале координат, начиная, например, с точки i и возвращаясь в эту же точку (рис.4).
i
z
1
Рис. 4.
Если бы мы наложили ограничения на аргумент: 0 2 , нам пришлось бы считать, что при подходе к точке 1 аргумент скачком переходит от значений сколь угодно близких к 2 , к значению 0, и это неестественно. Естественно считать, что аргумент изменяется непрерывно, но когда x yi возвращается в исходную точку, его аргумент получает
приращение, равное 2 . Впредь, говоря об аргументе комплексного числа, мы будем подразумевать какое либо его значение, безразлично какое. Если же возникает необходимость выбирать определенное значение, это приходится делать при помощи надлежащего описания (например, «возьмем наименьшее неотрицательное значение аргумента»).

z+w |
w |
z |
z–w |
