hitrov-1st-semester / Paragraf_4

§ 4. Системы двух и трех линейных уравнений с двумя и тремя неизвестными соответственно.

Цель настоящего параграфа не только научить решать системы двух и трех линейных уравнений с двумя и тремя неизвестными соответственно, что было бы достаточно просто, но и выявить те закономерности, изучение которых позволит в дальнейшем решать системы n уравнений с n неизвестными.

1. Система двух линейных уравнений с двумя неизвестными. Определитель матрицы второго порядка.

Рассмотрим систему двух линейных уравнений с двумя неизвестными с коэффициентами при неизвестных и свободными членами из некоторого поля P:

операции с равенствами. Именно, умножим первое равенство на a22 (коэффициент при x2 во втором уравнении), а второе – на (- a12 ) (минус коэффициент при x2 в первом

уравнении), и сложим левые и правые части полученных равенств. Выпишем полученный результат:

Поясним выражение (2). С помощью указанных выше операций над равенствами системы (1) (напомним, что x1 и x2 в (1) рассматриваются как решения) мы исключили в

(1) x2 . Чтобы подчеркнуть, что свободные члены b1 и b2 в выражении (2) связаны с x1 ,

мы ввели для них дополнительный нижний индекс – единица в скобках. Это понадобилось нам для того, чтобы увидеть достаточно полную аналогию выражения для коэффициента при x1 в левой части (2) с правой частью выражения (2).

Исключим теперь в (1) x1 . Для этого умножим первое равенство в (1) на (- a21 ), а второе на a11 и сложим полученные равенства. В итоге получим:

Из равенств (2) и (3) следует, что они имеют смысл при любых b1 и b2 , только если

Выражение в левой части (4) называется определителем матрицы коэффициентов системы (1). Его можно «оторвать» от системы, если связать его с произвольной матрицей второго порядка.

некоторого поля P называется выражение a11a22 a12a21 .

Определитель матрицы A, называемый также детерминантом матрицы A,

эквивалентны). С помощью этих обозначений определение 1 записывается, например, как:

Выражение (5) более «говорящее», чем определение 1. Оно, например, говорит, т.е. это хорошо видно, что определитель, есть некоторая функция на множестве матриц

второго порядка, сопоставляющая матрице число, равное сумме произведений элементов матрицы, называемых членами определителя, взятых по одному из каждой строчки и каждого столбца матрицы. Причем каждый из двух членов берется со своим знаком. Поскольку в матрице второго порядка можно построить только два произведения элементов взятых по одному из каждой строчки и каждого столбца, то определитель (правая часть выражения (5)) состоит из двух членов. Первый член есть произведение элементов расположенных на главной диагонали матрицы, идущей из левого верхнего угла в правый нижний, а второй член есть произведение элементов расположенных на побочной диагонали, идущей из верхнего правого угла в левый нижний. Первый член определителя берется со знаком плюс, а второй со знаком минус.

= -

Рис. 1.

То, что каждый член определителя представляет произведение элементов взятых по одному из каждой строчки и каждого столбца видно из индексов элементов, составляющих член определителя. Действительно, возьмем первый член определителя равный a11a22 . Мы видим, что первые индексы элементов составляющих этот член -

разные (элементы взяты по одному из каждой строчки) и вторые индексы – тоже разные (элементы взяты по одному из каждого столбца). То же самое мы увидим, если рассмотрим второй член определителя, т.е. если возьмем произведение a12a21 . Сравним

теперь наборы индексов двух членов. Наборы первых индексов в дух членах составляют одну и туже упорядоченную перестановку (1,2) из чисел 1 и 2. Наборы вторых индексов в этих членах составляют разные перестановки из тех же чисел – именно, перестановки (1,2) и (2,1). Следовательно, можно сделать вывод, что выбор знака при членах определителя, зависит каким-то образом от перестановки набора вторых индексов у сомножителей члена определителя при упорядоченном наборе первых индексов. При этом мы знаем, что первый член берется со знаком плюс, второй - со знаком минус. Полученных сведений об определителях второго порядка пока достаточно, чтобы, вопервых, иметь желание обобщить это понятие на определители третьего порядка и далее, во-вторых, ответить на вопрос о разрешимости системы (1), в-третьих, описать свойства

элементов множества M 2 .

Вернемся к системе уравнений (1). Из предположения, что решение (набор значений неизвестных, обращающих уравнения в равенства) системы существует, мы получили два равенства: (2) и (3). Из них следует, что

В (6), во-первых, мы избавились от индексов в скобках при свободных членах, поскольку они исполнили свою роль, во-вторых, ввели новые краткие обозначения. Мы обозначили через определитель матрицы A, через 1 - определитель, полученный из

определителя заменой первого столбца на столбец свободных членов, через 2 -

определитель, полученный из определителя заменой второго столбца на столбец свободных членов.

Глядя на формулы (6) мы видим следующее: для того чтобы решение системы (1) существовало при любом столбце свободных членов необходимо, чтобы определитель

Поскольку, для матриц из M 2 обратные к ним определяются единственным

A 1 (AX ) A 1B или X A 1B . То есть, столбец-решение X определяется единственным образом.

2. Системы трех линейных уравнений с тремя неизвестными. Определитель третьего порядка. Рассмотрим систему трех линейных уравнений с тремя неизвестными с коэффициентами и свободными членами из некоторого поля P:

Воспользуемся уже проделанным исследованием системы двух уравнений с двумя неизвестными, т.е. применим и здесь ту же схему исследования.

Предположим, что решение системы (14) существует, т.е. вместо неизвестных стоят уже конкретные числа, обращающие уравнения в равенства. Умножая левую и правую часть каждого равенства на некоторое одно и тоже для данного равенства число, и складывая полученные результаты-равенства, добьемся того, чтобы в левой части оставалась только одна переменная с некоторым коэффициентом. Другими словами будем в равенствах (14) последовательно исключать по две переменных.

Исключим в (14) переменные x2 и x3 . Чтобы увидеть сомножители, на которые нам нужно последовательно умножать первое, второе и третье равенства, поступим

оставшейся матрицы и будет тем числом, на которое мы умножим обе части первого равенства в (14).

Заметим, что при таком подборе множителей, на которые умножались равенства (14), коэффициенты при x2 и x3 обнулились (провести проверку!). Кроме того, видна явная аналогия между правой частью равенства (15) и выражением в фигурных скобках, являющимся коэффициентом при x1 . Правую часть равенства (15) можно получить из коэффициента при x1 , заменив в выражении для коэффициента элементы первого столбца

матрицы A соответствующими элементами столбца свободных членов. (15) служит равенством для определения x1 .

Проделав аналогичные исключения переменных x1 и x3 и, затем, переменных x1 и x2 мы получим выражения аналогичные (15) для определения x2 и x3 . Выпишем все три соотношения (включая и (15)) единообразным способом.

Обозначим выписанную систему соотношений как (16) и заметим, что в ней все выражения стоящие в фигурных скобках равны (проверить!). Назовем это общее значение определителем матрицы коэффициентов системы (14) или определителем матрицы третьего порядка, или, там где это не ведет к недоразумениям, просто определителем третьего порядка. Пользуясь матричным обозначением определителя третьего порядка (как это сделано для определителей второго порядка), запишем его определение в виде формулы:

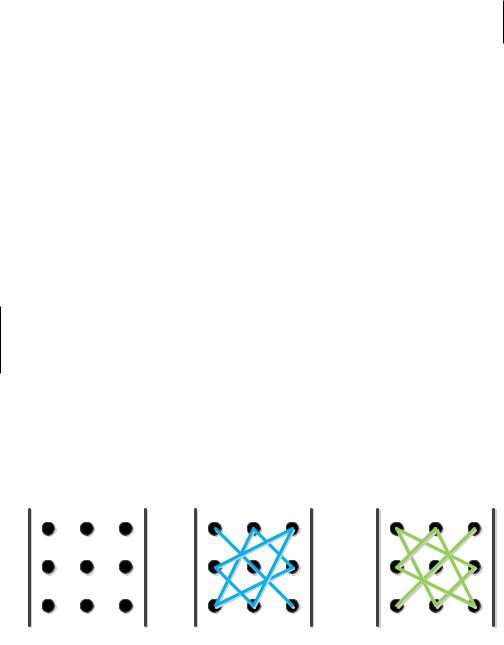
Как и для определителей второго порядка, каждое слагаемое, являющееся произведением элементов взятых по одному из каждой строчки и каждого столбца, будем называть членом определителя. Пользуясь «адресами» (индексами) каждому члену определителя мы можем сопоставить диаграмму (рисунок) на схеме матрицы. Диаграммы членов со знаком плюс лучше собрать на одной «картинке», а со знаком минус – на другой. Полученные две «картинки» и задают правило вычисления определителя третьего порядка.

При составлении правой части соотношения (17) мы свободно пользовались всеми известными со школы правилами сложения и умножения чисел, т.е. использовали структуру поля. Однако мы сознательно подчеркнули, что коэффициенты и свободные члены мы берем из некоторого поля P, т.е. будем для примеров вычисления определителей пользоваться не только вещественными или рациональными числами.

Отметим еще одну особенность упорядочения членов определителя. Элементы матрицы в члене определителя расположены так, что первые индексы элементов составляющих член определителя представляют собой упорядоченную перестановку из чисел 1, 2 и 3. При этом наборы вторых индексов пробегают все перестановки из чисел 1, 2 и 3, число которых, как известно равно 3!, т.е. равно 6. Занимательная задача для тех,

кто не знаком с теорией перестановок и подстановок, - найти правило, по которому каждой из 6 перестановок приписывается знак. Для этого желательно произвольной перестановке (i1,i2 ,i3 ) из первых 3 натуральных чисел, приписать по определенному

правилу неотрицательное целое число (i1,i2 ,i3 ) , так чтобы перестановкам,

соответствующим членам определителя, входящим в определитель со знаком (+), соответствовало четное число, а со знаком (-) - нечетное. Тогда знак члена определителя, связанный с перестановкой вторых индексов (i1,i2 ,i3 ) у составляющих его элементов,

равнялся бы ( 1) (i1 ,i2 ,i3 )

Полученное правило давало бы возможность новой записи определителя третьего порядка:

Обращаем внимание, что суммирование в правой части (18) ведется по всем перестановкам (i1,i2 ,i3 ) из чисел 1, 2, 3.

Вернемся вновь к соотношения (16), полученных нами при условии, что решение системы уравнений (14) существует. Перепишем систему равенств (16) в виде:

уравнений (14), т.е. выражение в фигурных скобках всех соотношений системы (16). Через

Резюмируем сказанное выше в виде теоремы.

Теорема (Крамера). Для того, чтобы решение системы трех уравнений с тремя неизвестными существовало и было единственным необходимо и достаточно, чтобы определитель матрицы коэффициентов системы был отличен от нуля. В последнем

случае решение находится по формулам Крамера: x1 1 , x2 2 . x3 3 .

Доказательство необходимости проведено выше (там мы исходили из того, что решение существует). Доказательство достаточности, т.е. проверку того, что при 0

рекомендуется провести самостоятельно. Мы же докажем теорему Крамера позже в общем случае.

Пример. Над полем рациональных чисел и полем по модулю три найти по формулам Крамера решение системы:

x1 x2 1 x1 x3 1

x1 x2 x3 1