
ТУ - лекции Шмырова / Лекции по ТУ / 25
.pdf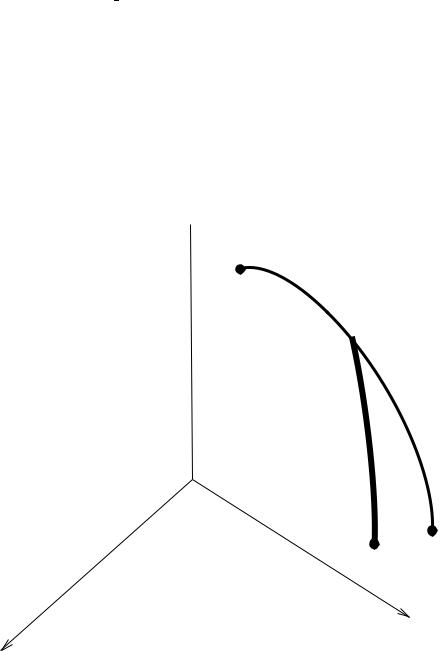
Лекция 25. Принцип динамического программирования. Функция Беллмана.
Одним из подходов к построению оптимального управления является теория Р. Беллама, носящая название "динамическое программирование". Базовой идеей метода динамического программирования является так называемый принцип оптимальности: кусок оптимальной траектории также является оптимальной траекторией. Приведем наглядную интерпретацию этого принципа.
Рассмотрим нелинейную управляемую систему вида
x = f(t; x; u); t 2 [to; T ]; x(t0) = x0;
с критерием качества
ZT
J(u) = f0(t; x; u)dt ! min
t0
На рисунке 1 приведем график оптимальной траектории x¤(t) на отрезке [t0; T ] è
обозначим его траектория (1-2). Также, на рисунке 1 присутствует траектория (1-2'), отличающаяся от оптимальной траектории (1-2) участком 2' (на временном отрезке
[t1; T ]).


Ðèñ. 1
107
По отношению к приведенному рисунку принцип оптимальности можно сформулировать следующим образом: Участок 2 оптимальной траектории (1-2), сам по себе является оптимальной траекторией системы x = f(t; x; u), состояние кото-
ðîé ïðè x(t1) = x1.
Действительно, если допустить противное, то существует траектория 2', достав- |
|
|
T |
ляющая функционалу J(u) = |
f0(t; x; u)dt значение меньшее, чем доставляет тра- |
|
t1 |
ектория 2. Но тогда на [t0; T ] |
оптимальной будет траектория (1-2'), а не (1-2), что |
R |
|
u( ), принимающих значение из множества U и определенных на промежутке времени
противоречит изначальной оптимальности траектории (1-2). |
|||
Обозначим через U (U содержится в Rr) множество значений, которые может |
|||
принимать управление |
|
, а через U |
обозначим множество измеримых функций |
[a;¢b]. |
u(t) |
e(a;b) |
|
Формализуем приведенный выше принцип оптимальности в рамках задачи с за- |
|||||||||
данным промежутком времени и со свободным правым концом. Управляемая система |
|||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
x = f(t; x; u(t)); |
t 2 [t0; T ]; |
x(t0) = x0; |
u(t) 2 U; |
(1) |
|||||
с критерием качества |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
J(u( )) = '(x(T )) + |
f |
|
t; x; u t |
dt |
! |
min |
(2) |
||
¢ |
Z |
|
0 |
( |
( )) |
|
u(¢)2U(t0;T) |
||
|
t0 |
|
|
|
|
|
|
e |
|
Пусть движение системы (1)-(2) происходит на временном отрезке t 2 [s; T ], òàê
÷òî t0 · s · t · T и начальное условие для x(t) в момент времени s имеет вид x(s) = x. Таким образом управляемая система имеет вид
x = f(t; x; u(t)); t 2 [s; T ]; x(s) = x; |
(3) |
с критерием качества
T
J |
|
|
u |
(¢)) = |
' |
x |
T |
|
Z |
f |
|
|
t; x; u t dt |
! |
min |
(4) |
|
1 |
( |
|
( |
( |
|
)) + |
|
0 |
( |
( )) |
u(¢)2U(s;T) |
||||
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
e |
|
Минимальное значение функционала (4) зависит от начального момента s и начального положения x(s) = x. Допустимым управлением в такой постановке является
e
измеримая функция u(¢) 2 U[s;T ], такая, что любого s 2 [t0; T ] существует реше-
ние задачи (3)-(4). e
U[s;T ] функциональное пространство функций u(¢) на временном промежутке [s; T ]. То, что в качестве допустимого управления следует рассматривать
именно измеримые функции, будет рассмотрено ниже.
Определение 1. Функция Беллмана. Функцией Беллмана B(s; x) называ-
ется функция, равная минимуму функционала (4) на траекториях системы (3) по всевозможным допустимым управлениям
B(s; x) = min |
0'(x(T )) + |
T |
f0(t; x; u(t))dt1 |
: |
|
|
|
|
|
¢ |
@ |
|
A |
|
e |
s |
|
||
u(¢)2U[s;T] |
|
Z |
|
|
108
Мы предположим что минимум в определении функции Беллмана достигается и соответствующее оптимальное управление обозначим через u(s; x; t), t 2 [s; T ].
Рассмотрим теперь произвольные моменты времени s è l, такие, что t0 · s · l · T . Формализует приведенный выше принцип оптимальности
|
|
B(s; x; ) = min |
0'(x(T )) + |
T f0(t; x; u(t))dt1 |
= |
|
|
||||||||||
|
|
|
|
|
u(¢)2U[s;T] |
@ |
|
|
|
|
Z |
|
|
A |
|
|
|
|
|
|
|
|
e |
|
|
|
|
s |
|
|
|
|
|
||
= |
min |
|
|
min |
0'(x(T )) + |
Z |
l f0(t; x; u(t))dt + |
T |
f0(t; x; u(t))dt1 |
= |
|
||||||
|
u(¢)2U[s;l] u(¢)2U[l;T] |
@ |
|
|
|
|
|
|
Z |
|
A |
|
|
||||
|
e |
|
|
e |
|
s |
|
|
|
|
|
l |
|
|
|
||
= |
min |
0 |
Z |
l f0(t; x; u(t))dt + |
min |
0 |
|
T |
f0(t; x; u(t))dt + '(x(T ))11 |
; |
|||||||
u(¢)2U[s;l] |
|
|
|
u(¢)2U[l;T] |
|
Z |
|
|
|
AA |
|
||||||
|
e |
@s |
|
|
|
|
e |
@l |
|
|
|
|
|
||||
откуда
B(s; x) = |
min |
0 l |
f0(t; x; u(t))dt + B(l; x(l))1 |
: |
(5) |
||||
|
|
e |
@s |
|
|
|
A |
|
|
|
|
u(¢)2U[s;l] |
Z |
|
|
|
|
|
|
Перепишем (5) в виде |
|
|
|
|
|
|
|
|
|
min |
0 l |
f0(t; x; u(t))dt + B(l; x(l)) |
|
B(s; x)1 |
= 0: |
(6) |
|||
e |
@s |
|
|
|
¡ |
A |
|
|
|
u(¢)2U[s;l] |
Z |
|
|
|
|
|
|
|
|
Предположим теперь, что момент времени l весьма близок к моменту s, функция Беллмана B дифференцируема в точке (s; x), а управление u(s; x; t) непрерывно по t в точке t = s. Тогда
B(l; x(l)) = B(s; x) + µ |
@B |
(s; x) + |
@B |
(s; x)f(s; x; u(s; x; s))¶(l ¡ s) + o(l ¡ s): |
|
|
|||
@t |
@x |
Устремляя в (6) l ! s+0, äåëÿ íà (l¡s) и переходя к пределу, получаем равенство
min |
µ |
@B |
(s; x) + |
@B |
(s; x)f(s; x; u) + f |
(s; x; u) |
= 0: |
(7) |
|
@t |
@x |
||||||||
u2U |
|
0 |
|
¶ |
|
Таким образом локализовав исследование функции Беллмана с помощью принципа оптимальности мы перешли от операции взятия минимума по функциональному пространству e
U[s;l], содержащейся в (6) к операции взятия минимума по подмножеству
Uевклидова пространства, содержащейся в (7). Краевое условие для функции B(t; x) имеет вид
B(T; x(T )) = '(x(T )): |
(8) |
Уравнение (7) называется уравнением Беллмана и следует из условий оптимального управления и гладкости функции B. Иными словами, если решение задачи по-
строения оптимального управления в задаче (1)-(2) существует и обладает свойством гладкости, то тогда справедливы уравнения (7)-(8)
109
