Эконометрика / Доп. материалы / TOBITмодели

TOBIT-модель. (модель с цензурированными и "урезанными" данными)

Модель была предложена Джеймосом Тобином (1958 г.) по результатам изучения расходов домохозяйств на товары длительного пользования.

Зависимая переменная часто бывает количественная и непрерывная, но ограничена на интервале своих значений (только положительные значения, заработная плата, продолжительность рабочего дня, расходы на определенные виды товаров, инвестиции и т.п.), т.е. есть ненаблюдаемые значения

Цензурированные наблюдения - известны значения независимых переменных

Урезанные наблюдения - известен лишь уровень "урезания", а

значения независимых переменных для исключенных из рассмотрения объектов неизвестны, т.е. выборка производится не из всех возможной совокупности наблюдений, а лишь из тех, что удовлетворяют каким-то ограничениям, как правило "урезание" происходит по "пороговому" значению зависимой переменной

Формальное представление tobit-модели

ПРИМЕР 1

y - зависимая переменная (расходы на транспорт), имеющая ограничения

z - другие потребительские расходы x - общие расходы

Индивид максимизирует уровень потребления, при соблюдении ограничения

maxU y, z

y,z

y z x

y 0, z 0

1

Задав функцию полезности можно найти решение задачи.

Транспортные расходы при оделенном стечении обстоятельств могут быть нулевыми (ограниченными).

При отсутствии ограничений на зависимую переменную расходы на транспорт составят (или желаемый уровень расходов на транспорт)

- y 0 1x

Наблюдаемы уровень равен 0, если желаемый отрицателен (в линейной модели)., т.е. потребители не будут пользоваться транспортом при отсутствии средств

TOBIT-модель с ЦЕНЗУРИРОВАННЫМИ данными

ОТЛИЧИЯ TOBIT-моделей от бинарных моделей:

разные способы установления связи между латентными и наблюдаемыми переменными

в тобит модели учитывается масштаб значение зависимых

переменных

в тобит модели в отличие от бинарных моделей отсутствует

необходимость в ограничениях по нормализации

в тобит модели рассматривается распределение зависимой

переменной только в положительной области

2

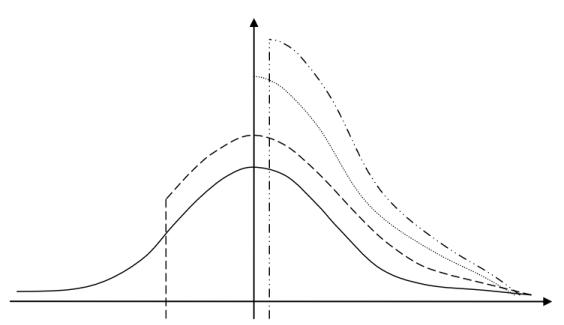
Модели с цензурированными данными представляют собой вариант регрессионных моделей. в которых все отрицательные значения

зависимых переменных установлены равными 0.

Пример графика плотности усеченного нормального распределения

3

МНК дает смещенные и несостоятельные оценки.

НЕОБХОДИМЫЕ СВЕДЕНИЯ

Z - случайная величина

F z - функция распределения Z

p z - плотность распределения случайной величины

a - любое число

Условное математическое ожидание Z при условии

Z a

с с с с

с - плотность стандартного нормального распределения

F с - функция стандартного нормального распределения

4

Выбираем только те наблюдения, для которых yi a

меньше соответствующего коэффициента

Среднее ошибок - с

дисперсия ошибок - 2 1 c

5

Для оценки используется ММП.

ФУНКЦИЯ ПРАВДОПОДОБИЯ

т.е. предельный эффект переменный (как в любой нелинейной модели)

6

РАСЧЕТЫ ПО TOBIT МОДЕЛИ

Все цензурированные наблюдения сохраняются в выборке, но вероятность того, что y 0 при заданных значениях объясняющих переменных в модели устанавливается :

Прогнозирование:

Влияние факторов. Расчет предельного эффекта

1) предельный эффект от изменения фактора на вероятность

2) предельный эффект изменения фактора на среднее

значение зависимой переменной

7

8

Модели с усеченными / урезанными выборками

(truncated regression model)

наблюдения полностью отсутствуют

значения зависимой переменной без ограничений попадают в отрицательную область или равны нулю:

yi 0 , то невозможно зафиксировать значения всех объясняющих переменных (зависимость заработной платы от стажа, если человек не работает, у него отсутствует заработная плата)

ФОРМАЛЬНАЯ ЗАПИСЬ МОДЕЛИ

N 0, 2

9

Варианты интерпретации коэффициентов тобит моделей в зависимости от формулировки задачи:

1. Если описание нулевых исходов представлено как вероятность того, что зависимая переменная равна 0:

тогда предельное изменение вероятности при изменении xik на небольшую величину (частная производная по xik )

k

- м.интерпретировать как предельный эффект изменений

xik в зависимости от вероятности наблюдения нулевых исходов

2. Усеченные данные

E yi yi 0 условное мат.ожидание зависимой переменной, при условии, что мат.ожидание положительно.

Цензурированный предельный эффект объясняющей переменной в зависимости от изменения объясняющей переменной xik зависит от ik

10