
- •Алгебра
- •Часть I
- •Свойства обратной матрицы:
- •Алгебра многочленов. Наибольший общий делитель двух многочленов (алгоритм Евклида).
- •Теорема Гаусса (основная теорема алгебры).
- •Наибольший общий делитель многочленов
- •Евклидовы и унитарные пространства. Теорема об ортогонализации. Ортонормированный базис.
-
Евклидовы и унитарные пространства. Теорема об ортогонализации. Ортонормированный базис.
Если длина вектора равна единице, он называется нормированным вектором:(x,x) = 1, |x| = 1.
Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.
Если векторы системы векторов e1, e2, ..., enпопарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (ei, ej) = 0, если i ≠ j ,(ei, ei) = 1.
Если e1, e2, ..., en — ортонормированная система и x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этой системе, то xi =(x, ei).
Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.
Если e1, e2, ..., en — ортонормированный базис n-мерного евклидова пространства и
x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этому базису, то координаты xi вектора x в ортонормированном базисе вычисляются по формулам xi =(x, ei), i = 1, 2, ..., n.
Теорема 1.1 (об ортогонализации) В евклидовом пространстве любой базис может быть преобразован к ортонормированному базису.
Доказательство.
Пусть дан произвольный базис в
![]() мерном
евклидовом пространстве:
мерном
евклидовом пространстве:
![]()
Построим следующие
системы,
![]() и
и
![]() векторов:
векторов:
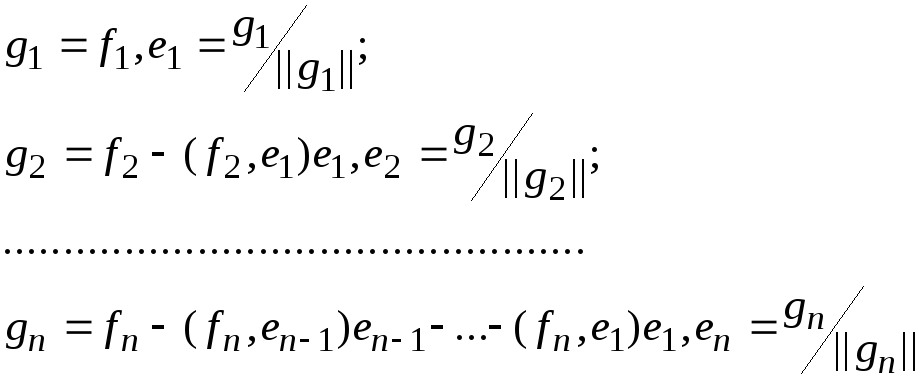
Докажем, что система
![]() ортогональна (тогда ясно, что система
ортогональна (тогда ясно, что система
![]() ортонормированная). Доказательство
проведем индукцией по
ортонормированная). Доказательство
проведем индукцией по
![]() .
Базис индукции очевиден, так как система,
состоящая из одного ненулевого вектора,
ортогональна по определению. Пусть для
некоторого
.
Базис индукции очевиден, так как система,
состоящая из одного ненулевого вектора,
ортогональна по определению. Пусть для
некоторого
![]() подсистема
подсистема
![]() ортогональна. Вычислим скалярное
произведение
ортогональна. Вычислим скалярное
произведение
![]() для
произвольного
для
произвольного
![]() .
.
Имеем:
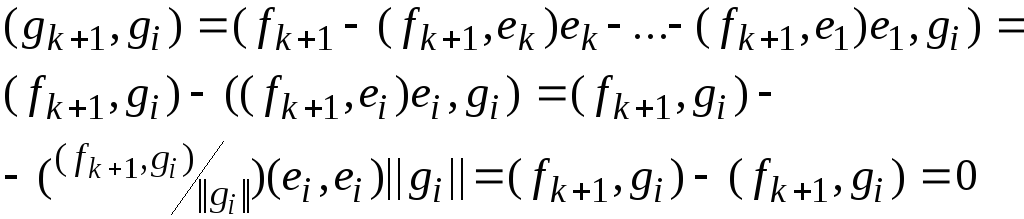
(мы учли, что для
любого
![]() скалярное произведение
скалярное произведение
![]() ).
).
Итак, система
![]() ортогональна, и теорема доказана.
ортогональна, и теорема доказана.
Базис конечномерного
евклидова пространства называется
ортонормированным базисом,
если образующие его векторы попарно
ортогональны и имеют единичную длину.
Поскольку доказано, что в любом
конечномерном евклидовом пространстве
существует ортонормированный базис,
будем рассматривать в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() только
ортонормированные базисы.
только
ортонормированные базисы.
Простейший пример
евклидова пространства дает нам
пространство
![]() --
пространство столбцов, в котором
скалярное произведение введено формулой
--
пространство столбцов, в котором
скалярное произведение введено формулой
 .
.
Тогда для любых
![]() ,
,
![]() из
из
![]() справедливы
формулы:
справедливы
формулы:

Все евклидовы
пространства размерности
![]() устроены
так же, как пространство
устроены
так же, как пространство
![]() .
.
Величины
![]() ,
,
![]() и
и
![]() характеризуют
взаимное расположение векторов и не
зависят от выбранного ортонормированного
базиса.
Если
характеризуют
взаимное расположение векторов и не
зависят от выбранного ортонормированного
базиса.
Если
![]() и
и
![]() --
два ортонормированных базиса в
--
два ортонормированных базиса в
![]() -мерном
евклидовом пространстве, то матрица
перехода от одного из этих базисов к
другому -- ортогональная матрица.
-мерном
евклидовом пространстве, то матрица
перехода от одного из этих базисов к
другому -- ортогональная матрица.
