4. Математическое описание плоских геометрических проекций

Каждую из проекций можно описать матрицей 44. Этот способ оказывается удобным, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования.

Центральная (перспективная)проекция получается путем перспективного преобразования и проецирования на некоторую двухмерную плоскость «наблюдения». Перспективная проекция на плоскостьZ = 0 обеспечивается преобразованием

[X Y Z H] = [x y z 1]* = [x y 0 (rz+1)].

Рис. 3.40. Вычисление одноточечной перспективы

или x*==;

y*==;

z*==,

где r=.

Центр проекции находится в точке с координатами (0,0,-k) (рис. 3 .40.), плоскость проецированияZ = 0. Соотношения междуx, yиx*, y*остаются теми же самыми. Рассматривая подобные треугольники, получим, что

=, или x* =;

аналогично y* = .

Координаты x*, y*являются преобразованными координатами. В перспективном проектировании преобразованное пространство не является евклидовым, так как ортогональность осей не сохраняется. Приk =получим аксонометрическое преобразование.

Аффинное преобразование есть комбинация линейных преобразований, сопровождаемых переносом.

Последний столбец в обобщенной матрице 44 должен быть равен, в этом случаеH = 1.

Перспективному преобразованию может предшествовать произвольная последовательность аффинных преобразований. Таким образом, чтобы получить перспективные изображения из произвольной точки наблюдения вначале используют аффинные преобразования, позволяющие сформировать систему координат с осью Zвдоль желаемой линии визирования. Затем применяется перспективное преобразование.

Аналогично перспективное преобразование, когда картинная плоскость перпендикулярна оси Zи совпадает с плоскостьюZ= 1/r. Центр проекции находится в центре координат:

[X Y Z H] = [x y z 1] *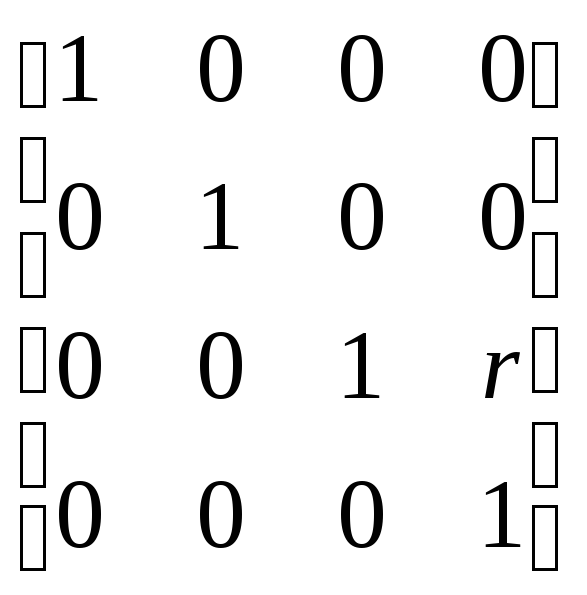= [x y z (rz+1)]— одноточечная перспектива (точка сходаZ);

— точка сходаX.

Двухточечная (угловая) перспектива. Для получения двухточечной перспективы в общей матрице преобразования устанавливают коэффициентыpиq:

(x', y', z', 1) = (x, y, z, 1)=[x, y, 0, (px+qu+1)];

(x', y', z', 1) = .

Такое преобразование приводит к двум точкам схода. Одна расположена на оси X в точке (, 0, 0, 1), другая на осиYв точке (0,, 0, 1).

Рассмотрим это преобразование на получение проекции единичного куба (рис. 3 .41.).

Рис. 3.41. Единичный куб для получения двухточечной проекции

.

В результате получаем проекцию вида, представленного на рис. 3 .42.

Рис. 3.42. Двухточечная проекция единичного куба

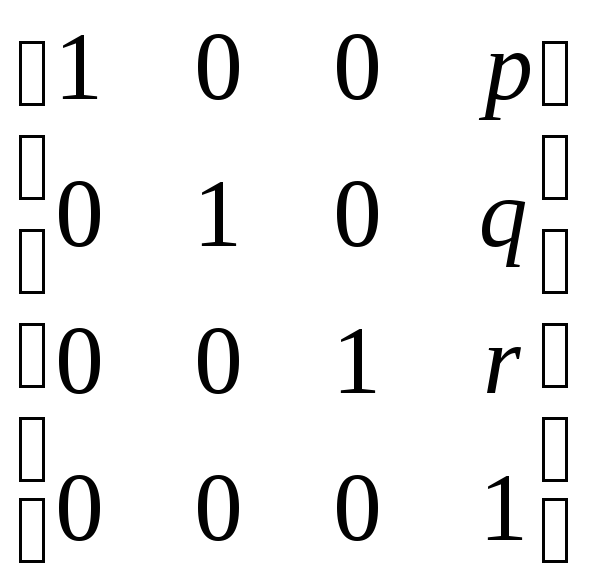=[x y z (px+qy+rz+1)] — трехточечная (косая) перспектива.

Для того чтобы создать диметрическую проекцию, необходимо выполнить следующее условие:

sin²φ=sin²θ/(1-sin²θ).

Одним способом выбора sinθ является сокращение оси Zв фиксированное число раз. При этом единичный вектор на осиZ, равный [0 0 1 1], преобразовывается к виду

[X Y Z H] = [sinφ -cosφsinθ cosφcosθ 1]

или x* = sinφ;

y*= - cosφ sinθ.

Таким образом, для диметрической проекции получаем

φ = 20,705:

θ = 22,208.

Для образования изометрической проекциинужно в одинаковое число раз сократить все три оси. Для этого необходимо, чтобы выполнялось условие

sin²φ=sin²θ/(1- sin²θ) и sin²φ=(1-2sin²θ)/(1- sin²θ).

Таким образом,

φ = 35,26439;

θ = 45.

Рассмотрим теперь косоугольную проекцию (рис. 3 .43.), матрица может быть записана исходя из значенийиl.

Проекцией точки P(0,0,1) является точкаP(l cos,lsin, 0), принадлежащая плоскостиxy. Направление проецирования совпадает с отрезкомРР, проходящим через две эти точки. Это направление естьР-Р= (lcos,lsin, -1). Направление проецирования составляет уголс плоскостьюxy.

Теперь рассмотрим проекцию точки x, y, zи определим ее косоугольную проекцию (x_p y_p) на плоскостиxy:

x_p = x + z(lcos);

y_p = y + z(lsin).

Таким образом, матрица 44, которая выполняет эти действия и, следовательно, описывает косоугольную проекцию, имеет вид

М_кос=.

Рис. 3.43. Вычисление косоугольных проекций

Применение матрицы М_кос приводит к сдвигу и последующему проецированию объекта: плоскости с постоянной координатойz = z₁переносятся в направленииx наz₁ l cosи в направленииy наz₁ l sinи затем проецируется на плоскостьz = 0. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных осиz.

Для проекции Кавальеl = 1, поэтому угол = 45. Для проекции Кабинеl=½, а= arctg(2) = 63,4. В случае ортографической проекцииl = 0 и= 90, поэтому матрица ортографического проецирования является частным случаем косоугольной проекции.