Лабораторная работа № 1 Исследование особенностей формирования собственного теплового излучения подстилающей поверхности

Излучение абсолютно черного тела

Из опыта известно, что все вещества непрерывно излучают электромагнитные волны. Это электромагнитное излучение охватывает практически весь диапазон длин волн. Вследствие природы своего формирования такое излучение получило название собственного теплового излучения, так как по современным представлениям порождается переходом молекул вещества в возбужденной состояние за счет кинетических взаимодействий (столкновений) с последующим возвращением в невозбужденное состояние с излучением кванта света. Поэтому понятно, что интенсивность собственного теплового излучения должна быть связана с внутренней энергией вещества, которая в состоянии термодинамического равновесия прямо пропорциональна температуре, и должна зависеть от его физического строения.

Законы формирования поля собственного теплового излучения, позволяющие получить важную для решения задач дистанционного зондирования аналитическую форму зависимости количества излучаемой объектом на различных длинах волн и в различных направлениях лучистой энергии от параметров, характеризующих его физическое состояние, весьма просты лишь для случая идеального поглотителя и идеального излучателя электромагнитных волн – абсолютно черного тела (АЧТ).

Абсолютно черным телом называется идеальное тело, которое испускает максимальное излучение для данной температуры, при этом не отражает и не пропускает энергии, поглощая внутри себя всё падающее излучение. Причем это свойство справедливо для излучения, соответствующего всем длинам волн и всем углам падения. Понятие абсолютно черного тела является основным при изучении переноса энергии теплового излучения. Являясь идеальным излучателем, абсолютно черное тело используется в качестве эталона, с которым сравнивается излучение реальных тел и для калибровки спектральных приборов в ИК-области спектра.

В 1901 г. Планк сделал два допущения о свойствах атомных осцилляторов с целью теоретического объяснения распределения по спектру излучения нагретой полости. Во-первых, Планк постулировал, что энергия гармонического осциллятора описывается выражением

где f - частота осцилятора;

h - постоянная Планка;

n - квантовое число, которое может принимать только целые значения.

В дальнейшем было показано, что в действительности вместо значения n необходимо использовать значение n + 1/2, однако это не отразилось на правильности полученного конечного выражения для излучения нагретой полости.

Во-вторых, Планк постулировал, что осцилляторы излучают энергию не постоянно, а скачками - квантами. Эти кванты энергии испускаются, когда осциллятор переходит из одного квантового энергетического состояния в другое.

На основе этих двух допущений Планк смог теоретически вывести так называемую функцию Планка, определяющую спектральную яркость излучения абсолютно черного тела (АЧТ), которая играет важную роль при расчете интенсивности собственного теплового излучения системы "подстилающая поверхность - атмосфера". Спектральная яркость АЧТ в диапазоне волновых чисел  и  + d определяется посредством количества лучистой энергии dE, излучаемой элементом поверхности АЧТ dS за интервал времени dt в телесном угле (здесь опущено указание об угле, поскольку излучение АЧТ подчиняется закону Ламберта, т.е. поверхность АЧТ является идеальной диффузной поверхностью). В соответствии с законом Планка спектральная яркость АЧТ в вакууме является функцией только двух переменных: абсолютной температуры АЧТТ и волнового числа (либо эквивалентных характеристик: ):

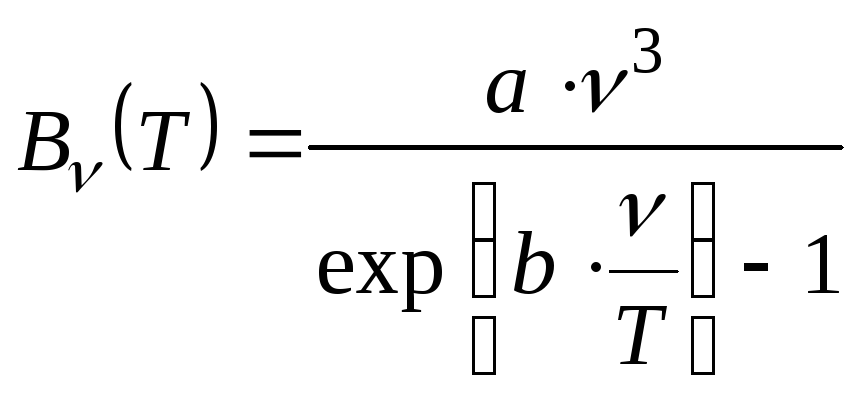, (2.1)

где , [см ^{- 1}] - волновое число (  - длина волны [мкм] );

Т - абсолютная температура АЧТ, [К];

=1.19105  10^-4 , [ Вт/ (м²  ср  см^-1) / (см^-1)³ ];

=1.43874 [ К/см^-1 ].

В терминах длины волны  функция Планка может быть записана следующим образом:

(2.2)

где =1.90 10⁸ , [т/ (м²  мкм  ср )  (мкм)⁵ ];

=1.43874 10⁴ , [К  мкм ].

В терминах частоты функция Планка имеет следующий вид:

, (2.3)

где =/ - частота, Гц (= 2.9996 10¹⁴ [мкм/с] - скорость света).

Для коротких длин волн (начиная с ближней инфракрасной области  < 2 мкм) для спектральной яркости АЧТ справедливо с высокой точностью приближение Вина:

(2.4)

Начиная с микроволновой области спектра ( >100 мкм) для спектральной яркости АЧТ выполняется приближение Релея-Джинса:

(2.5)

Интегрируя функцию Планка по всем частотам (волновым числам или длинам волн), получаем полный радиационный выход энергии АЧТ: F(T). Полученное таким образом соотношение известно как закон излучения Стефана-Больцмана:

, (2.6)

Где  =5.6693  10^-8 [т/ (м²  К⁴) ] - постоянная излучения Стефана-Больцмана.

Длина волны, на которой при заданном значении температуры АЧТ () функция Планка достигает своего максимума, определяетсязаконом смещения Вина:

, [мкм] (2.7)

Где = 2897.8, [мкм К].

И, наконец, из (2.1) выражение T:

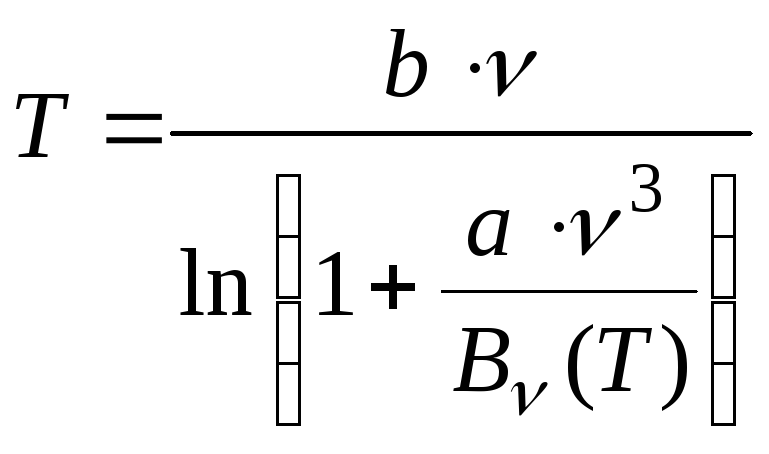, (2.8)