2. Вывод основного уравнения радиолокации.

Одноволновой метод основан на измерении комплекса радиолокационных характеристик метеообъектов. Однако этот метод не позволяет определить ослабление электромагнитной волны на трассе распространения и внутри метеорологического объекта.

В основу одноволнового метода положено уравнение дальности радиолокационного наблюдения метеорологических объектов. Оно связывает между собой технические характеристики метеорологических объектов, определяющие их отражающие свойства и возможную дальность обнаружения объектов.

Рассмотрим РЛС, которая осуществляет приём потока излучения (мощность радиоэха) от отдельной частицы (гидрометеора).

,

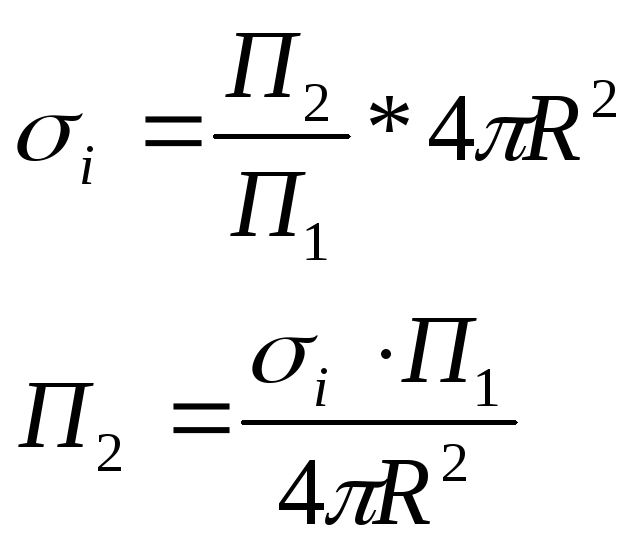
где Р₁- мощность, принимаемая от отдельного гидрометеора или импульсная мощность информационного сигнала от отдельной частицы; П₂- плотность потока мощности, рассеянной от частицы вблизи РЛС; П₁- плотность потока мощности, падающей на гидрометеор; R- расстояние от радиолокатора до гидрометеора; S_A- реальная площадь раскрыва антенны, (D- диаметр антенны),.

Здесь приняты два упрощения. В виду малости телесного угла метеоцели можно пренебречь зависимостью эффективной площади рассеяния от направления, и заменить интегрирование умножением плотности потока мощности на величину площади раскрыва антенны. Второе упрощение связано с заменой эффективного диаметра антенны геометрическим.

Введем в режим излучения антенной РЛС коэффициент направленного действия К_н:

,

где Р₀- импульсная мощность передатчика РЛС без учета потерь.

Подставим данное выражение в предыдущее:

Для получения мощности радиоэха от ансамбля гидрометеоров необходимо просуммировать информационные сигналы от всех частиц, расположенных в разрешаемом объеме, который может быть определён с помощью соотношения:

,

где θ- ширина диаграммы направленности; с- скорость распространения радиоволны; τ- длительность зондирующего импульса.

Поток рассеянного излучения от импульсного объёма будет складываться от частиц с различными ЭПР, находящихся в разрешаемом объеме:

,

где N(σ_i)- спектр распределения частиц по ЭПР.

,

где .

Подставив вместо Р₁ и V_р соответствующие выражения, получаем уравнение радиолокации метеорологического объекта(4):

В метеорологических РЛС (МРЛ), как правило, применяются антенны с асимметричными диаграммами направленности. Для таких антенн коэффициент направленного действия может быть определен:

;

.

Если приближенно считать, что , то уравнение радиолокации можно переписать в следующем виде:

Введем постоянную радиолокатора С_р/л :, тогда в уравнение радиолокации, показывающее отношение информационного сигнала, мощность излучаемого сигнала:

Если отнести отношение информационного сигнала к уровню собственных шумов приемника, то данное уравнение будет иметь вид:

,

где .

Получившееся выражение является уравнением радиолокации метеообъектов, где мощность принимаемых сигналов определяется относительно уровня мощности собственных шумов приемника. Тогда удельная ЭПР:

в [1/м]

или в [мм⁶/м³].

Тогда уравнение удельной ЭПР имеет вид:

и,

где z_r и z_d- отражаемость, выраженная через радиус и диаметр соответственно.

Если использовать выражение отражающих свойств объекта через z, то уравнение радиолокации метеообъектов можно записать в виде:

Потенциал радиолокатора выражается(5):

Потенциал РЛС определяется только её техническими характеристиками и может быть заранее рассчитана. Если расстояние до объекта выразить в [км], а отражаемость в [мм⁶/м³], то размерность потенциала РЛС будет выражена в (6).

Для практических расчётов основное уравнение радиолокации метеообъектов можно переписать в виде:

Максимальная дальность обнаружения метеообъектов определяется выражением:

,

где - чувствительность приемной станции.

Как видно из последнего уравнения отмечается зависимость максимального расстояния от отражающих свойств объекта z_d и от чувствительности приемника радиолокационной станции.

При выводе одноволнового уравнения радиолокации сделаны упрощения:

1. рассматривалось распространение плоской электромагнитной волны в свободном пространстве без учёта рефракции. При учёте реальных условий распространения необходимо ввести множитель < 1;

2. не учитывалось ослабление электромагнитной волны на пути распространения. Для учёта ослабления необходимо в правую часть ввести коэффициент < 1;

3. предполагалось, что весь разрешаемый объем пространства заполнен рассеивающими частицами. В реальных условиях необходимо ввести коэффициент заполнения ≤ 1;

4. считалось, что рассеяние электромагнитной волны некогерентное и однократное.

В действительности наблюдается интерференция полей от отдельных элементарных рассеивателей, что приводит к существенному изменению величины принимаемых сигналов. Этот эффект можно учесть введением соответствующего поправочного коэффициента в правую часть уравнения радиолокации метеообъектов. С учётов возможных предположений одноволновое уравнение можно переписать в виде:

или ,

где - комплексный коэффициент, который учитывает все упрощения которые мы вводим. Он зависит от длины волны и свойств окружающей волны.

Таким образом, два последних уравнения позволяют по величине измеренного отраженного сигнала определить отражаемость метеорологических объектов, находящихся на определенном расстоянии от РЛС:

В виду сложного распространения отражаемостей в вертикальном и горизонтальном направлениях, возможно получить дополнительные характеристики вертикального и горизонтального профиля отражаемости, т. е. пространственные и временные градиенты отражаемости.