ЛК3_Аппроксимация
.docx
Аппроксимация и интерполяция данных. Основные определения
Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Например: зависимость числа оборотов двигателя от нагрузки, т.е. n=f(Мкр.); зависимость силы резания при обработке детали на металлорежущем станке от глубины резания, т.е. P=f(t), и т.д.
Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости в виде функции n=f(Мкр.), P=f(t), y=f(t).
Однако на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, измеряются значения параметров на выходе системы. Результаты измерений заносятся в таблицу.
Таким образом, в результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию.
Далее с этой табличной функцией необходимо вести научно-исследовательские расчеты. Например, необходимо проинтегрировать или продифференцировать табличную функцию и т.д.
При такой постановке задачи моделирования нужно заменить табличную функцию аналитической. Для этой цели используются методы аппроксимации и интерполяции.
Аппроксимация – это замена исходной функции f(x) функцией φ(x) так, чтобы отклонение f(x) от φ(x) в заданной области было наименьшим. Функция φ(x) называется аппроксимирующей.
Если исходная функция f(x) задана таблично (дискретным набором точек), то аппроксимация называется дискретной. Если исходная функция f(x) задана аналитически (на отрезке), то аппроксимация называется непрерывной или интегральной.
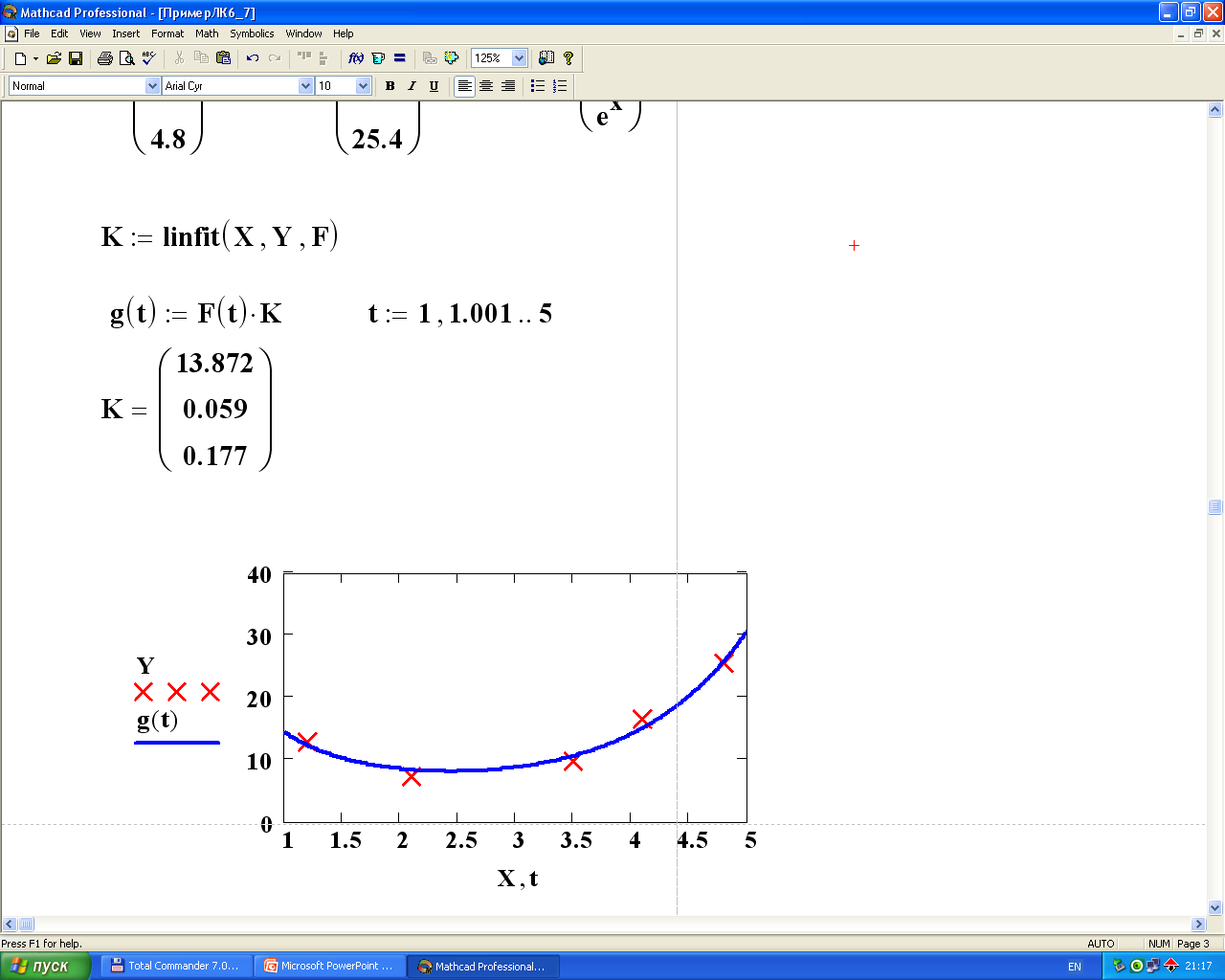
Интерполяция – это замена исходной функции f(x) функцией φ(x) так, чтобы φ(x) точно проходила через точки исходной функции f(x).
Интерполяция еще называется точечной аппроксимацией.
Точки исходной функции f(x) называются узлами интерполяции.
Для интерполирующей функции справедливо

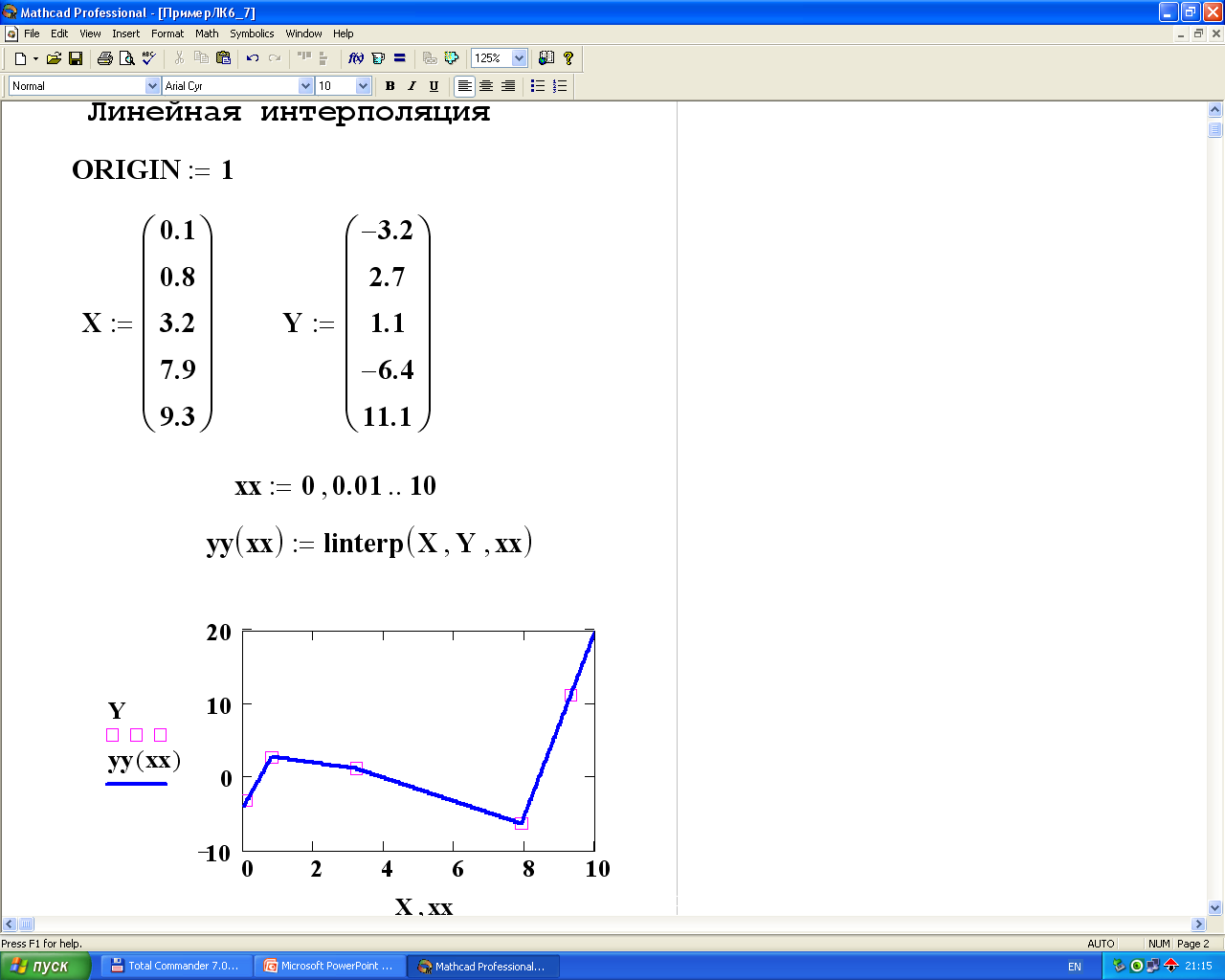
Экстраполяцией называется аппроксимация вне заданной области определения исходной функции, т.е.
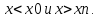
Найдя интерполяционную функцию, мы можем вычислить ее значения между узлами интерполяции, а также определить значение функции за пределами заданного интервала (провести экстраполяцию).
Основной мерой отклонения функции y(x) от функции f(x) при аппроксимации является величина, равная сумме квадратов разностей между значениями аппроксимирующей и исходной функций

Простейшими видами интерполяции является линейная и квадратичная.
При линейной интерполяции точки заданной функции соединяются линейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках. В качестве уравнения интерполяционного многочлена используются уравнения прямой, проходящей через две точки.
При квадратичной интерполяции в качестве приближающей функции, соединяющей соседние точки, принимается квадратный трехчлен. Такая интерполяция называется параболической.
Распространенным видом интерполяции является интерполяция с использованием кубических сплайн-функций.
Сплайн представляет собой модель гибкого тонкого стержня из упругого материала, закрепленного в двух соседних узлах интерполяции с заданными углами наклона α и β так, чтобы потенциальная энергия стержня была минимальна.

Интерполяция может выполняться с помощью многочленов Ньютона, Эрмита, Лагранжа и т.д.
Наиболее известными методами аппроксимации являются метод наименьших квадратов, метод многочленов Чебышева, рядов Тейлор и т.д.
При решении задач аппроксимации часто используются функции регрессии.
Регрессия – представление совокупности данных некоторой функцией f(x).
Задачей регрессии является вычисление параметров функции f(x) таким образом, чтобы функция приближала последовательность исходных точек с наименьшей погрешностью. При этом функция f(x) называется уравнением регрессии.
При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки.
Аппроксимация и интерполяция данных в MathCad
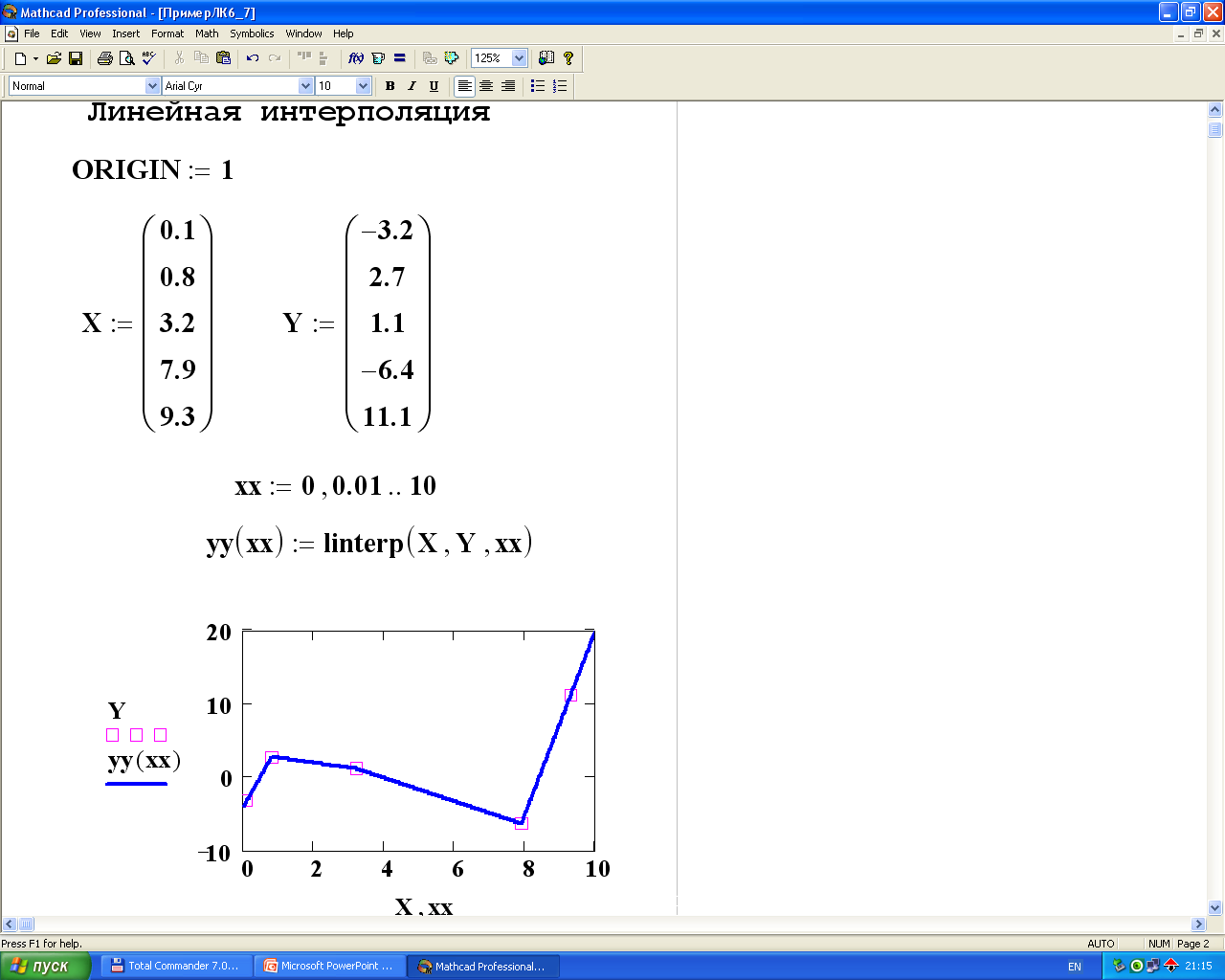
Линейная интерполяция осуществляется с помощью встроенной функции linterp, имеющей следующий общий вид:
linterp(VX,VY,x),
где VX, VY – векторы координат узловых точек;
x – значение аргумента, для которого будет получено интерполяционное значение функции y.
В MathCAD для проведения кубической сплайн-интерполяции предлагается три встроенные функции (VX, VY – вектора узловых точек):
cspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к кубическому полиному;
pspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к параболической кривой;
lspline(VX, VY) – возвращает вектор вторых производных (VK) при приближении в опорных точках к прямой.
Интерполирующая функция строится с помощью стандартной функции interp, имеющей следующий общий вид:
interp(VK,VX, VY,x),
где
VK – вектор вторых производных сплайна в опорных точках;
x – произвольная точка, в которой вычисляется значение интерполирующей функции.
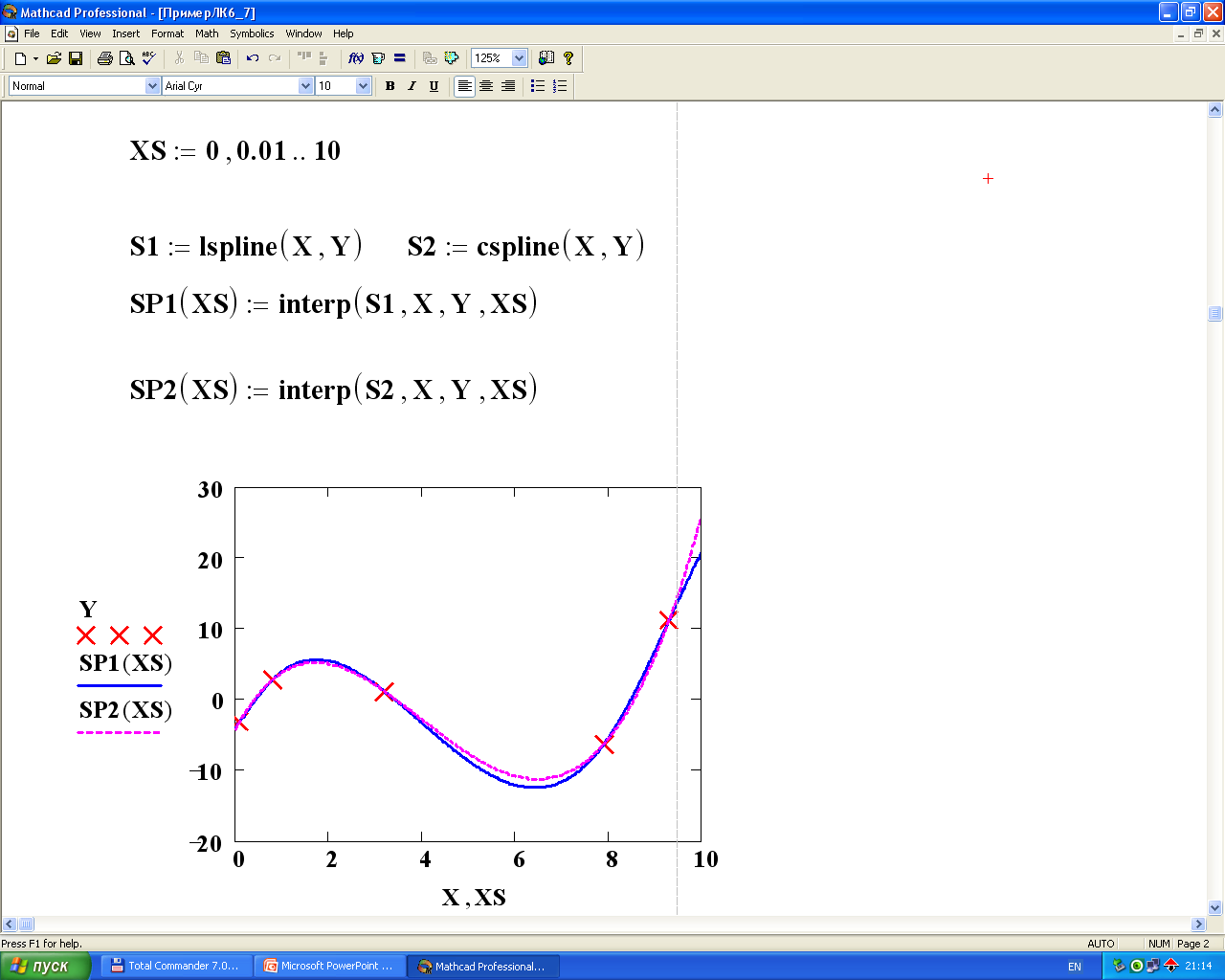
Последовательность кубической сплайн-интерполяции такова:
- создаются вектора VX и VY, содержащие координаты точек, через которые нужно провести кубический сплайн;
- вычисляется вектор VK с использованием одной из перечисленных функций;
- вычисляется множество произвольных значений интерполирующей функции в нужном количестве точек с помощью стандартной функции interp.
MathCAD позволяет проводить линейную регрессию общего вида, в которой аппроксимирующая функция задается линейной комбинацией функций, причем сами функции fi(x) могут быть нелинейными:

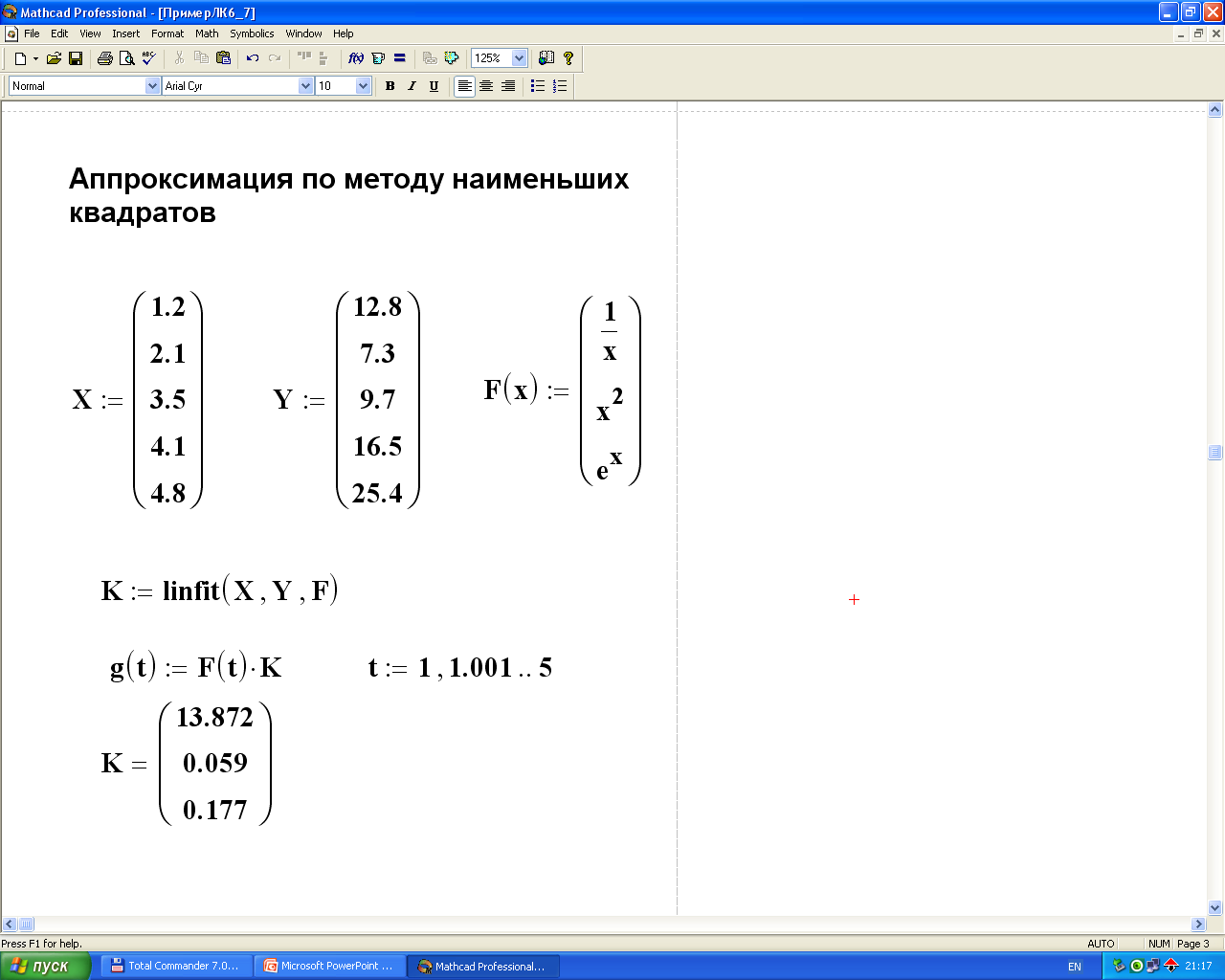
Линейная регрессия общего вида реализуется с помощью функции linfit:
linfit(VX, VY,F),
где
VX, VY – координаты исходных точек;
F - вектор, содержащий функции fi(x) , записанные в символьном виде.
Функция linfit еще называется функцией аппроксимации по методу наименьших квадратов.
Результатом работы функции linfit является вектор коэффициентов К, при котором среднеквадратичная погрешность приближения исходных точек с координатами VX, VY, минимальна.
Вектор VX должен быть возрастающим.

Полиномиальная регрессия позволяет аппроксимировать зависимость полиномом произвольной степени.
Вычисление коэффициентов полинома осуществляется с помощью встроенной функции regress, которая имеет следующий общий вид:
regress(VX, VY, n),
где
VX, VY – вектора с координатами исходных данных,
n – порядок полинома (первые три возвращаемые коэффициенты служебные, а далее искомые значения, расположенные по возрастанию степени полинома).
Для построения аппроксимирующей зависимости можно воспользоваться встроенной функцией
interp(VK,VX, VY,x),
где VK – вектор коэффициентов, рассчитанных функцией regress;
x – рассчитываемая точка.
Для проведения регрессии необходимо что бы вектор VX был возрастающим и количество его элементов было больше степени полинома на 1. Функция regress определяет единственный приближающий полином, элементы которого вычисляются по всей совокупности точек.
Для выполнения нелинейной регрессии общего вида необходимо определить параметры произвольной аппроксимирующей функции, при которой обеспечивается минимальная среднеквадратичная ошибка.
Для этого используется встроенная функция genfit, имеющая следующий общий вид:
genfit(VX,VY,VS,F),
где
VS - вектор, который задает начальные приближения элементов вектора K, рассчитываемых итерационным способом;
F - вектор, который содержит искомую функцию и ее частные производные по параметрам Ki в аналитическом виде:
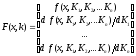
На рисунке приведены примеры применения различных видов аппроксимирующих функций в MathCad.
|
|
|
|