1 введение

6

Литература.

1. Математика для экономистов: учебное пособие / С.И. Макаров. – М.: КНОРУС, 2008.

2. Высшая математика для экономистов: учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. – М.: ЮНИТИ, 2001.

3.Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: учебник: в 2-х ч.. – М.: Финансы и статистика, 2003.

4. Математика для экономистов. Задачник:учебно-практическое пособие / кол. авторов; под ред. С.И. Макарова, М.В. Мищенко. – М.: КНОРУС, 2008.

Лекция 1.

Математическая символика

Логические символы

- для любого, любой

- существует

: - такой, что

- и

- или

- следует

- тогда и только тогда (необходимо и достаточно)

┐- символ отрицания

Теоретико-множественные символы

- объединение

- пересечение

- разность

С – дополнение

- включается, входит

- принадлежит

- пустое множество

Элементы теории множеств

Множество – совокупность элементов, объединенных по какому-либо признаку.

А={}

Пусть А, В, С – некоторые множества. Тогда над ними можно совершать следующие операции:

1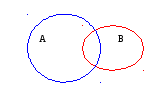. Объединение множеств:

.

2. Пересечение множеств:

.

3. Разность множеств:

.

4. Дополнение множества в другом множестве:

.

Самостоятельно: свойства операций над множествами.

Стандартные множества

N = {1, 2, 3, …} – натуральные числа

Z = { N , N , 0} – целые числа

P = {, где Z , N,- взаимно простые} – рациональные числа

(конечные или периодические десятичные дроби)

Q – иррациональные числа (бесконечные непериодические десятичные

дроби)

R = { P Q } – действительные числа.

Элементы множества R называются собственными точками;

- несобственные точки.

Виды промежутков:

- отрезок

- интервал

, - полуинтервал.

Абсолютная величина числа

Опр. Абсолютной величиной (модулем) действительного числа х называется само число х, если оно неотрицательно и противоположное ему число –х, если оно отрицательно:

R ,

Свойства модуля:

1.

2.

3.

4.

5.

6. , ().

7. Первое неравенство треугольника: R:

.

Второе неравенство треугольника: R:

.

Окрестность точки

Понятие окрестности точки вводится по следующему определению.

Опр. 1. Если - собственная точка, то окрестностью точки х₀ называется множество точек х, удовлетворяющих условию: .

Поясним геометрический смысл этого понятия. Раскроем знак модуля:

,

,

.

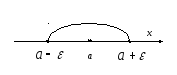
Таким образом, окрестность точки х₀ представляет собой совокупность точек , удаленных от х₀ на расстояние, не превосходящее .

Опр.2. Если , то то окрестностью точки х₀ называется множество точек х, удовлетворяющих условию: .

Опр.3. Если , то то окрестностью точки х₀ называется множество точек х, удовлетворяющих условию: .

Опр.4. Если , то то окрестностью точки х₀ называется множество точек х, удовлетворяющих условию: .

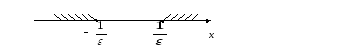
Понятие функции

Пусть Х и У – некоторые множества.

Опр. Если каждому элементу ставится в соответствие по некоторому правилу единственный элемент , то говорят, что на множестве Х задана функция (функциональная зависимость) со значениями в множестве У:

, .

Множество Х называется областью определения функции и обозначается D(f), множество У называется областью значений функции и обозначается I(f).

В мат. анализе рассматривают в основном числовые функции, т.е. такие, где Х и У – множества действительных чисел.

Если функция f переводит элемент в элемент , то х называют независимой переменной или аргументом или прообразом элемента у, у называют зависимой переменной или значением функции или образом элемента х. Для функциональной зависимости образ всегда единственен.

Способы задания функций (задать множества и описать правило):

- аналитический, с помощью одной или нескольких формул:

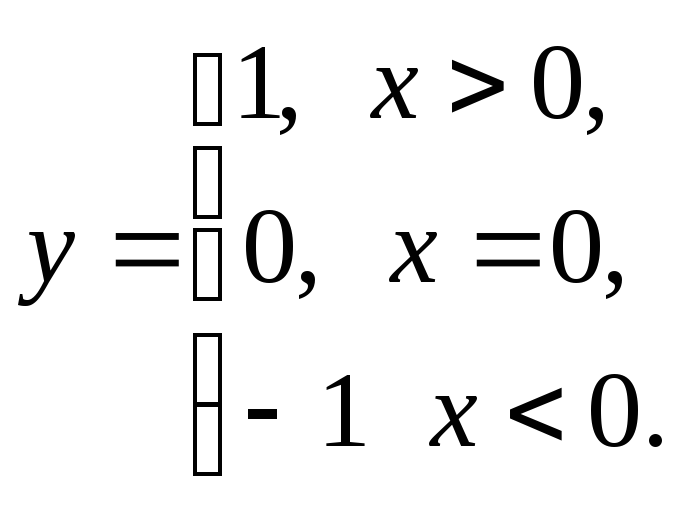
- табличный:

Год	1800	1930	1960	1975	1987	2000
Численность населения (млрд)	1	2	3	4	5	6

- графический (ЭКГ);

- словесный (функция Дирихле 1-рац., 0-иррац.);

- (читается «у равно антье х») целая часть – наибольшее число, не превосходящее х.

Например, .

Функция называется явной, если она задана формулой, разрешенной относительно зависимой переменной. Если функция задана уравнением, не разрешенным относительно зависимой переменной, то говорят, что функция задана неявно.

()

Опр. Композицией отображений и называется отображение .

Например, ;

;

.

Композицию числовых функций называют сложной функцией или функцией от функции.

Опр. Если обратное соответствие, переводящее Y в X является функцией, т.е. у каждого элемента имеется единственный прообраз , то это соответствие называют обратным отображением или обратной функцией к функции :

, .

Пример. Рассмотрим функцию при x0.

Выразим х: , . Обратной функцией будет являться .

Т.к. традиционно независимую переменную обозначают х, то, переобозначив переменные, получим обратную функцию .

Обратная функция к обратной функции совпадает с исходной функцией: .

Обратная функция существует для любой строго монотонной функции.

Опр. Графиком числовой функции y=f(x) называется совокупность точек плоскости вида (x,f(x)), где .

Графики обратных функций симметричны относительно биссектрисы I и III координатных углов.

Некоторые свойства функций.

Опр. Числовая функция y=f(x) называется монотонно возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции:

.

Опр. Числовая функция y=f(x) называется ограниченной сверху на множестве А, если найдется число М такое, что:

.

Опр. Числовая функция y=f(x) называется ограниченной снизу на множестве А, если найдется число М такое, что:

.

Опр. Числовая функция y=f(x) называется ограниченной на множестве А, если найдется число К такое, что:

.

В противном случае функция называется неограниченной.

Числовая функция y=f(x) называется четной, если ; числовая функция называется нечетной, если .

Числовая функция y=f(x) называется периодической, если найдется такое число Т>0, что .

Элементарные функции и их классификация.

К основным элементарным функциям относят: линейную, степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции.

Опр. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и/или конечного числа операций образования сложной функции, называются элементарными.

Пример. Неэлементарные: .

Элементарные функции делят на алгебраические и трансцендентные.

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий (например, полином, дробно-рациональная функция, иррациональная функция). Остальные – трансцендентные (показательная, логарифмическая, тригонометрические и обратные тригонометрические функции).

Знать свойства и графики основных элементарных функций.

Преобразования графиков функций

1. - симметричное отображение относительно оси Ох.

2. - симметричное отображение относительно оси Оу.

3. - параллельный перенос на а влево/ вправо.

4. - параллельный перенос на а вверх/ вниз.

5. - растяжение (для к>1) /сжатие (для 0<к<1) в к раз вдоль оси Оу.

6. - растяжение (для 0<к<1) /сжатие (для к>1) в к раз вдоль оси Ох.

7. - часть графика, расположенная ниже оси Ох, отображается симметрично относительно оси Ох, остальная часть графика не изменяется.

8. - часть графика, расположенная в правой полуплоскости копируется в левую полуплоскость.