Задания по статистике / Гипотеза о нормальном законе распределения

Проверка гипотезы о нормальном

распределении генеральной совокупности

Во многих практических задачах точный закон распределения исследуемой случайной величины неизвестен. Требуется найти теоретический закон распределения случайной величины, опираясь на эмпирическое распределение этой величины, полученное в результате выборочного наблюдения. Для решения этой задачи выдвигается некоторая гипотеза о виде закона распределения. Эта статистическая гипотеза может быть выдвинута на основе:

а) выполнения условий центральной предельной теоремы;

б) опыта предшествующих исследований;

в) графического изображения эмпирического распределения (например, вид гистограммы частостей может свидетельствовать в пользу нормального закона распределения случайной величины).

Проверка гипотезы о виде закона распределения производится с помощью специально подобранной случайной величины, называемой критерием согласия.

Имеется несколько критериев согласия: c² («хи-квадрат») Пирсона, Колмогорова, Смирнова, Романовского и др.

Критерий Пирсона c² - наиболее часто употребляемый критерий согласия. Его достоинство в том, что он может быть использован для проверки гипотезы о любом законе распределения. Рассмотрим применение c²-критерия для проверки гипотезы о нормальном распределении генеральной совокупности.

Пусть дана генеральная совокупность, элементы которой обладают признаком Х (случайная величина Х), закон распределения которой неизвестен. Но есть основания предположить, что Х имеет нормальный закон распределения, то есть выдвинуть нулевую гипотезу Н₀: генеральная совокупность имеет нормальное распределение. В качестве конкурирующей гипотезы Н₁ выберем гипотезу: признак Х имеет распределение, отличное от нормального.

Проверим гипотезу Н₀ при заданном уровне значимости .

Для этого произведем выборку объемом n, в результате получим эмпирическое (выборочное) распределение (интервальный ряд для непрерывного признака X):

х0-х1	х1-х2	х2-х3	...	хi-1-хi	...	хs-1-хs
			...		...		,

где (х_i-1 - х_i ) - частичный интервал;

- эмпирические частоты, то есть число значений (наблюдений) признака Х, попавших в соответствующий частичный интервал:

Для вычисления теоретических частот применим статистическое определение вероятности: . Откуда , где n - объем выборки.

Теоретическая вероятность (частость) вычисляется здесь в предположении, что генеральная совокупность Х имеет нормальное распределение. Для непрерывного признака X теоретическая вероятность представляет собой вероятность попадания случайной величины Х в частичный интервал . Таким образом,

,

где Ф(t) - функция Лапласа, выборочная средняя и выборочное среднее квадратическое отклонение - оценки параметров предполагаемого нормального распределения, найденные по выборке объема n.

Можно показать, что для дискретного признака теоретическую вероятность находят следующим образом:

,

где ; - дифференциальная функция нормированного нормального распределения, шаг - выборочная средняя; - выборочное среднее квадратическое отклонение.

Итак, найдены теоретические частоты данного распределения в предположении, что оно подчиняется нормальному закону.

Как правило, между эмпирическими и теоретическими частотами распределения имеются расхождения. В некоторых случаях эти расхождения не являются существенными и обусловлены либо малым числом наблюдений, либо способом их группировки, либо иными причинами. В других случаях расхождение частот неслучайно (существенно) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Для того чтобы дать обоснованный ответ о случайном или неслучайном расхождении эмпирических и теоретических частот, применим критерий Пирсона (критерий c ²). В качестве меры расхождения между эмпирическими и теоретическими частотами будем рассматривать специально подобранную случайную величину:

,

где - эмпирические частоты, найденные по данным выборочного наблюдения;

- теоретические частоты, найденные в предположении справедливости гипотезы Н₀.

Примем без доказательства, что закон распределения случайной величины c ² при увеличении объема выборки () независимо от того, какому закону распределения подчинена генеральная совокупность Х, стремится к закону распределения c ² ("хи-квадрат") с k степенями свободы. Число степеней свободы находят из равенства k=s-r-1, где s - число частичных интервалов, r - число параметров предполагаемого распределения, которые оцениваются по данным выборки. В нашем случае предполагают нормальное распределение, значит, оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), отсюда r=2, поэтому k=s-3.

При проверке нулевой гипотезы о законе распределения генеральной совокупности строится правосторонняя критическая область . Границу раздела областей и - точку находят из условия , где - заданный уровень значимости и k - число степеней свободы.

Критическая точка отделяет область малых расхождений эмпирических и теоретических частот (то есть область принятия гипотезы ) от области значительных суммарных расхождений и (или критической области W). Критические точки , удовлетворяющие указанному условию, при разных уровнях значимости и различных степенях свободы k приведены в прил. 4. Далее по данным наблюдения вычисляют фактическое значение критерия . Если эмпирические частоты в целом слабо отличаются от теоретических частот , то , вычисленное по данным выборки, будет близко к нулю. Если же в целом значительно отклоняются от , то величина становится достаточно большой. Таким образом, величина характеризует суммарное расхождение между эмпирическими и теоретическими частотами, найденное по данным выборки.

Если наблюдаемое значение критерия попало в область принятия гипотезы (<(a, k), как показано на рис. 1(а), то нет оснований отвергать нулевую гипотезу, по данным наблюдения признак Х имеет нормальный закон распределения, расхождение между эмпирическими и теоретическими частотами случайное.

Если наблюдаемое значение критерия попало в критическую область (>(a, k), как показано на рис. 1(б), то нулевая гипотеза отвергается, принимается как наиболее правдоподобная конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между эмпирическими и теоретическими частотами значимо.

а) б)

Рис. 1

Итак, чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:

1) по данным выборки объема n найти теоретические частоты ;

2) найти наблюдаемое значение критерия ;

3) из таблицы критических точек распределения c ² (прил. 4 файла «Приложения») по заданному уровню значимости a и числу степеней свободы k=s-3 найти (a, k) - границу правосторонней критической области (рис. 1);

4) сравнить с (a, k) и сделать вывод.

Замечание 1. Необходимые условия применения критерия Пирсона:

1) объем выборки должен быть достаточно велик, по крайней мере не менее 50 наблюдений;

2) каждый частичный интервал должен содержать не менее пяти наблюдений. Если это количество в отдельных интервалах мало, то имеет смысл объединить некоторые интервалы, суммируя частоты.

Замечание 2. Очевидно, что при проверке гипотезы о законе распределения контролируется лишь ошибка первого рода.

Пример 1. Используя критерий Пирсона при уровне значимости 0,05, установить, случайно или значимо расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения о нормальном распределении признака Х генеральной совокупности:

	14	18	32	70	20	36	10
	10	24	34	80	18	22	12	.

Решение. Выдвигаем нулевую Н₀ и конкурирующую Н₁ гипотезы.

Н₀: признак Х имеет нормальный закон распределения.

Н₁: признак Х имеет закон распределения, отличный от нормального.

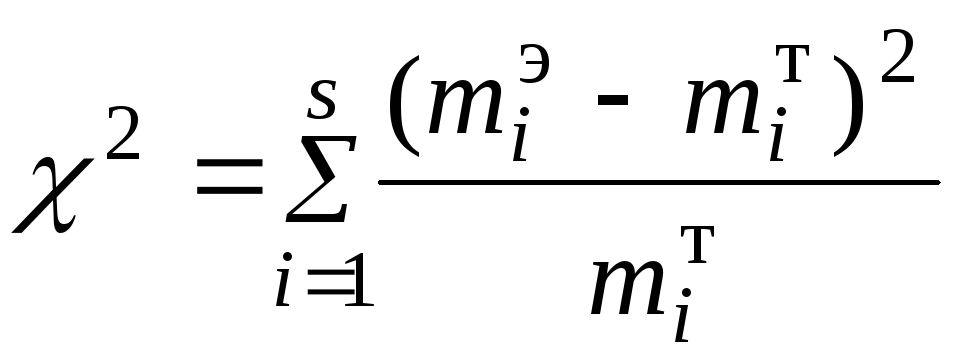В данном случае рассматривается правосторонняя критическая область . Проверим гипотезу Н₀ с помощью случайной величины , которая имеет распределение c ² с k = s- -3 = 7-3 = 4 степенями свободы. Вычислим наблюдаемое значение критерия c ² по выборочным данным. Расчеты представим в таблице:

	14 18 32 70 20 36 10	10 24 34 80 18 22 12	1,6 1,5 0,118 1,25 0,222 8,909 0,333
Итого	200	200	13,932

 » 13,93; (0,05; 4) = 9,5. Сравниваем и (0,05; 4).

Так как >(0,05; 4), то есть наблюдаемое значение критерия попало в критическую область (рис. 1(б)), нулевая гипотеза отвергается, принимается конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, а расхождение между эмпирическими и теоретическими частотами значимо.

Пример 2. Установить закон распределения признака Х - затраты времени на обработку одной детали.

Затраты времени на обработку 1 детали, Х, мин: xi-1-xi	Число рабочих, mi
22-24 24-26 26-28 28-30 30-32 32-34	2 12 34 40 10 2
Итого	100

Решение. Признак Х - затраты времени (мин) на обработку одной детали. Выдвигаем нулевую и конкурирующую гипотезы.

Н₀: признак Х имеет нормальный закон распределения.

Н₁: признак Х имеет закон распределения, отличный от нормального.

Для проверки гипотезы Н₀ сделана выборка объемом n = 100, и по данным выборки найдены выборочные характеристики: _в = 28 мин, s_в = 1,93 мин. Гипотеза проверяется с помощью случайной величины , которая имеет распределение c ² с k = s - 3 = 6 - 3= степенями свободы. Предварительно определим теоретические частоты по формуле

.

Расчеты представим в таблице:

xi			xi-1
24 26 28 30 32 34	-2,07 -1,04 0 1,04 2,07 3,11	-0,4807 -0,3508 0 0,3508 0,4807 0,49901	22 24 26 28 30 32	-3,11 -2,07 -1,04 0 1,04 2,07	-0,49901 -0,4807 -0,3508 0 0,3508 0,4807	1,83»2 12,99»13 35,08»35 35,08»35 12,99»13 1,83» 2
Итого	-	-	-	-	-	99,8»100

Вычислим наблюдаемое значение критерия, расчеты запишем в таблице:

	2 12 34 40 10 2	2 13 35 35 13 2	0 0,08 0,03 0,71 0,69 0
Итого	100	100	1,51

Итак,  = 1,51; (0,01; 3) = 11,3. Сравниваем и (0,01; 3).

Так как <(0,01; 3), то есть наблюдаемое значение критерия попало в область принятия гипотезы (рис. 1(а)), то нет оснований отвергать нулевую гипотезу, данные наблюдений согласуются с выдвинутой гипотезой о нормальном законе распределения генеральной совокупности Х. Расхождение между эмпирическими и теоретическими частотами случайное.

Итак, по данным выборки признак Х - затраты времени на обработку одной детали - имеет нормальный закон распределения.