9. Функция одного случайного аргумента

Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X и записывают .

Рассмотрим правила для нахождения закона распределения СВ Y по известному закону распределения СВ X .

Пусть аргумент X - дискретная случайная величина, с законом распределения:

X	X1	X2	…	Xn
P	p	p	…	p

Если различным значениям СВ X соответствуют различные значения СВ Y, то вероятности соответствующих значений равны; если же различным значениям СВ X соответствуют значения СВ Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.

Математическое ожидание функции

.

Пусть аргумент X - непрерывная случайная величина, заданная плотностью распределения f(х).

Если функция - дифференцируемая строго монотонная, обратная функция которой, то плотность распределенияg(у) случайной величины Y находится по формуле

.

Если функция в интервале возможных значенийX не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция (х) монотонна, и найти плотности распределений(у) для каждого из интервалов монотонности, а затем представитьg(у) в виде суммы

Например, если функция (х) монотонна в двух интервалах, в которых соответствующие обратные функции равныито.

Математическое ожидание и дисперсия функции непрерывного случайного аргумента

или

ПРИМЕР 9.1. Дискретная случайная величина X задана законом распределения

X	-1	0	1	2
P	0,1	0,2	0,4	0,3

Найти закон распределения случайной величины и ее математическое ожидание.

Решение. Найдем возможные значения Y:

Возможному значению Y = 4 соответствуют возможные значения X = -1 и Х=1, поэтому Р(Y = 4) = Р(Х = -1)+ Р(Х = 1) = 0,1 + 0,4 = 0,5. Вероятности возможных значений Р(Y=3)=Р(Х=0)=0,2; Р(Y=7)=Р(Х=2)=0,3.

Итак, искомый закон

Y	3	4	7
P	0,2	0,5	0,5

ПРИМЕР 9.2. Дана нормально распределенная случайная величина X с m = 0 и = 1. Найти закон распределения СВY=X+2 .

Решение. По условию задачи

Так как Y = Х + 2, то (х) = х + 2. Найдем для(х) обратную функциюТогда плотность распределения случайной величиныY будет иметь вид

.

ПРИМЕР 9.3. Нормально распределенная случайная величина X имеет плотность

Найти плотность распределения g(у) случайной величины у = х².

Решение. Функция у=х² на не монотонна. Интервалы монотонности (;0) и (0;+). На интервале (;0) обратная функция

.

Тогда

Так как у = х², причем , то. Таким образом,

ПРИМЕР 9.4. Случайная величина X задана плотностью

Найти математическое ожидание случайной величины Y = 3Х + 5.

Решение. I способ: Найдем М(Х) =

По свойствам математического ожидания

II способ: Воспользуемся формулой . Тогда

10. Предельные теоремы теории вероятностей

Неравенство Чебышева. Для любой случайной величины X, имеющей математическое ожидание m и дисперсию , справедливы неравенства:

.

Теорема Чебышева. Если - попарно независимые случайные величины с конечными математическими ожиданиями, дисперсии которых ограничены одним и тем же числомС, то есть

то

.

Если математические ожидания всех случайных величин равны, то есть , то

.

Замечание. Для случайных величин с равными математическими ожиданиями теорему Чебышева можно записать в виде

с равными дисперсиями

.

Теорема Бернулли. Пусть X – число «успехов» в схеме Бернулли с n испытаниями, р – вероятность «успеха» в одном испытании. Тогда для любого > 0,

.

Замечание 1. Учитывая замечание к теореме Чебышева, теорему Бернулли можно записать:

.

Замечание 2. Так как величина достигает максимума 0,25 при0,5, то

.

Центральная предельная теорема в грубой формулировке выглядит так: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

Сформулируем более точно.

Теорема. Пусть - независимые случайные величины с математическими ожиданиямии дисперсиями, причем то при закон распределения случайной величины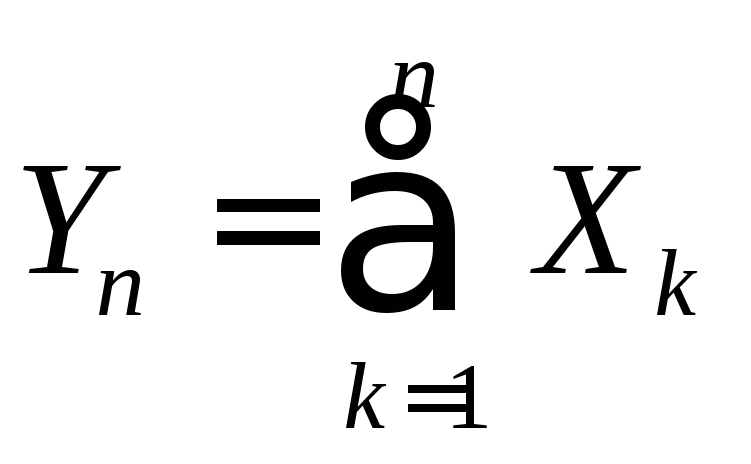неограниченно приближается к нормальному.

ПРИМЕР 10.1. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется: а) меньшее двух; б) не меньше двух.

Решение. а) Пусть X - дискретная случайная величина, характеризующая число отказавших элементов за время Т. Тогда

М(Х) = np = 10∙0,05 = 0,5; D(Х) = npq = 10∙0,05∙0,95 = 0,475.

Воспользуемся неравенством Чебышева

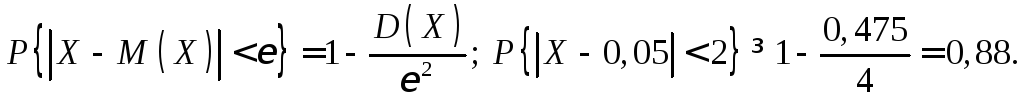
б) События ипротивоположны, поэтому

ПРИМЕР 10.2. Гнутая монета подбрасывается 100 раз. Герб выпал 70 раз. Оценим вероятность выпадения герба для этой монеты.

Решение. Возьмем = 0,1. Тогда получим

, то есть с вероятностью 0,75 оцениваемое значение р принадлежит интервалу < 0, ;

0,1 < 0,7 - р < 0,1; 0,6 < р < 0,8.

Для = 0,2 получим 0,5 <р < 0,9 с вероятностью не менее 0,9375.

В качестве оценки р берем относительную частоту .

При увеличении числа испытаний n мы будем получать с вероятностью, близкой к единице, все более маленькие интервалы для оценки теоретической вероятности р.

ПРИМЕР 10.3. По полосе укреплений противника сбрасывается 100 серий бомб. При сбрасывании одной такой серии математическое ожидание числа попаданий равно 2, а среднее квадратическое отклонение числа попаданий равно 1,5. Найти приближенно вероятность того, что при сбрасывании 100 серий в полосу попадает от 180 до 220 бомб.

Решение. Представим общее число попаданий как сумму чисел попаданий бомб в отдельных сериях:

, где - число попаданийi-й серии.

Будем считать число n = 100 достаточным для того, чтобы можно

было применить предельную теорему. Имеем: CB X подчинена нормальному закону распределения.

ПРИМЕР 10.4. Последовательность независимых случайных величин ,... задана законом распределения

		0
P

Применима ли к заданной последовательности теорема Чебышева?

Решение. Проверим конечность математических ожиданий и равномерную ограниченность дисперсий.

.

Таким образом, каждая из случайных величин имеет конечное математическое ожидание.

.

		0
P

;

.

Так как все дисперсии равны, то они равномерно ограничены числом . Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.

ПРИМЕР 10.5. В кассе учреждения имеется сумма d = 3500 (руб.). В очереди стоит n = 20 лиц. Сумма X, которую надо выплатить отдельному лицу - случайная величина с математическим ожиданием m = 150 (руб.) и средним квадратическим отклонением = 60 (руб.).

Найти вероятность того, что суммы d не хватит для выплаты денег всем людям, стоящим в очереди.

Решение. На основании центральной предельной теоремы для одинаково распределенных слагаемых при большом n (а n = 20 практически можно считать «большим») случайная величина , где- сумма, которую надо выплатитьi-му лицу, имеет приближенно нормальное распределение с параметрами

Суммы Y не хватит, следовательно, Y > 3500.

Итак, с вероятностью около 3% имеющейся в кассе суммы не хватит для выплаты всем, стоящим в очереди.

26