Лекция 12. Реляционная алгебра (часть 1).

План лекции

1. Реляционная алгебра и реляционное исчисление.

2. Операции реляционной алгебры.

3. Объединение отношений.

4. Разность отношений .

5. Декартово произведение отношений .

6. Пересечение отношений.

7. Выборка.

8. Создание проекций.

9. Примеры использования операций.

В 1970-71 г.г. Кодд опубликовал статьи, в которых ввел в рассмотрение понятие реляционную алгебру и реляционное исчисление.

Реляционная алгебра – это процедурный язык обработки реляционных таблиц. Это означает, что в реляционной алгебре используется пошаговый метод в создании реляционных таблиц, со Реляционная алгебра

держащих ответы на запросы.

Реляционное исчисление – это не процедурный язык, т.е. язык позволяющий сформулировать, что нужно сделать, а не как этого добиться.

Операции реляционной алгебры. Операции реляционной алгебры манипулирует реляционными таблицами, для создания новых таблиц, затем полученные новые таблицы, могут использоваться в качестве исходных таблиц для новой операции.

Рассмотрим типовые операции.

1. Объединение отношений (u).

R:=R1 U R2

R - это имя , присвоенное полученной в результате таблице, сострящей из тех строк, которые находятся либо в таблице R1, либо в таблице R2, либо в них обеих.

Операция применяется к отношениям одной и той же арности. Таблицы должны иметь одни и те же столбцы, т. е. у них совпадают как количество столбцов, так и области значений столбцов. Такие таблицы называют объединительно – совместительными (Рис.).

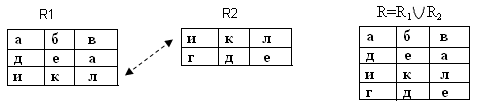
Рис.1. Объединение отношений

Например, это:

R1 – информация о сотрудниках одного отдела,

R2 – информация о сотрудниках другого отдела,

R – информация о всех сотрудниках.

Повторяющаяся запись отображается один раз.

2. Разность отношений (-).

R:=R₁ - R₂

Разностью отношений называется множество кортежей, принадлежащих R₁ , но не принадлежащих R₂ .

Т.е. идентифицируются строки, которые есть в одной таблице, но отсутствуют в другой.

Например, находим разность отношений R1 и R2, взятых из предыдущего примера (рис.2.).

Рис.2. Разность отношений

3. Декартово произведение отношений (*).

R:=R₁*R₂

Если отношение R₁ имеет арность К₁, а отношение R₂ арность К₂, то декартовым произведением отношений R₁ и R₂ является множество кортежей, арности (К₁+К₂). Причем первые К₁ элементов, образующие кортеж, берутся из отношения R₁, а последние К₂ элементов – из отношения R₂ (Рис.3, Рис. 4 ).

Рис.3. Декартово произведение отношений

Рис.4. Декартово произведение отношений

Еще один пример операции декартова произведения

Первая таблица «Сотрудники отдела»

Фамилия

Иванов

Петров

Вторая таблица «График обследования»

Обследование	Дата
Сердечно-сосудистой системы	1.12.09
Желудочно-кишечного тракта	8.12.09

Результирующая таблица

«Прохождение обследования »

Фамилия	Обследование	Дата
Иванов	Сердечно-сосудистой системы	1.12.09
Иванов	Желудочно-кишечного тракта	12/08/09
Петров	Сердечно-сосудистой системы	1.12.09
Петров	Желудочно-кишечного тракта	08.12.09