Если бы все точки границы были бы правильными, то

: |-z₀|=R- граница круга сходимости

()>0: z |-z|<()

заметим, что часть этого круга лежит вне круга сходимости исходного степенного ряда.

Т.о. аналитическая функция f(z) может быть аналитически продолжена с помощью степенного ряда хоть немного (), но за пределы круга |-z₀|=R. Т.о. она является аналитичной в “большем” круге, а следовательно граница круга сходимости может быть “отодвинута дальше чем R”.

Следствие. Радиус сходимости степенного ряды аналитической функции равен расстоянию от центра разложения до ближайшей особой точки. Это можно использовать для определения радиуса сходимости, например, ряды

Центр разложения z=0, ближайшая особая точка z=-1 – точка ветвления функции .

§23. Ряд Лорана.

1. Кольцо сходимости ряда Лорана.

Определение. Рядом Лорана называется степенной ряд вида (суммирование ведется и по положительным, и по отрицательным степеням), здесьz₀ – фиксированная точка комплексной плоскости.

Второе слагаемоеназываетсяправильной (регулярной) частью ряда Лорана, первое -главной частью ряда Лорана.

Очевидно, областью сходимости ряда Лорана будет пересечение областей сходимости его регулярной и главной части.

Из теоремы Абеля следует, что регулярная часть сходится в круге и является в нем аналитической функцией. C^(|z-z₀|<R₁).

Сделаем замену 1/(z-z₀)=; главная часть ряда Лорана принимает вид . По теореме Абеля такой ряд сходится при, что соответствует внешности круга.

При R₂<R₁ существует общая область сходимости - круговое кольцо R₂<|z-z₀|<R₁. Свойства степенного ряда, следующие из теоремы Абеля :

1. C^(R₂<|z-z₀|<R₁).

2. Внутри кругового кольца сходимости ряд Лорана можно почленно дифференцировать и интегрировать любое число раз, при этом полученные ряды также аналитичны в том же кольце.

3. R₁ определяется через {c_n}, n=0,1,2...,: R₁=1/L₁, L₁= 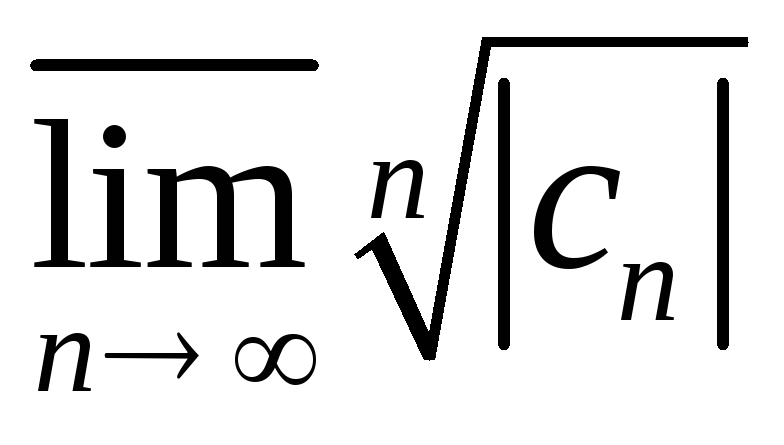или L₁=, а R₂ - через {c_-n}, n=1,2...,: R₂=, или R₂=.

4. Коэффициенты ряда Лорана c_n через значения суммы ряда в точке z₀ не определяются! В точке z₀ сумма ряда Лорана не определена!

Пимеры:

1. ,

2. ,

3. ,

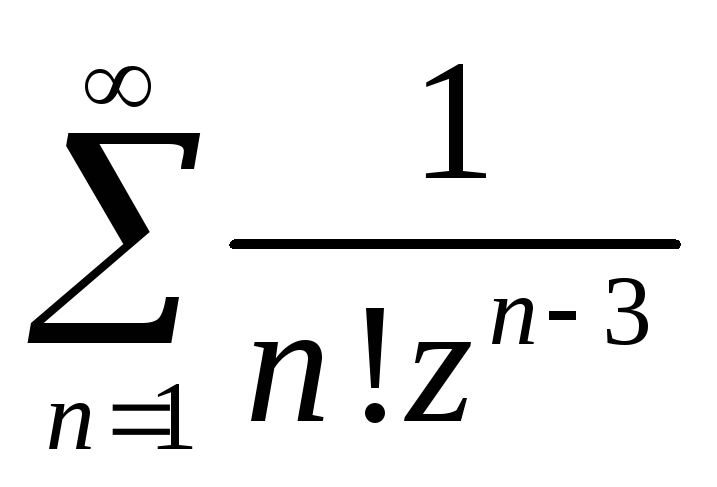2. Теорема о разложении функции комплексной переменной, аналитической в круговом кольце в ряд Лорана.

Теорема (теорема Лорана) Если f(z)C^(R₂<|z-z₀|<R₁), то она однозначно разложима в этом кольце в ряд Лорана f(z)= .

Доказательство. Фиксируем произвольную точку z внутри кольца: (R₂<|z-z₀|<R₁) и построим окружности C₁ :|-z₀|=R'₁ и C₂ : |-z₀|=R'₂ , с центром в точке z₀ и радиусами R'₁ и R'₂ : R₂<R'₂<|z-z₀|<R'₁<R₁.

По формуле Коши для многосвязной области в силу аналитичности f(z), справедливо

f(z)==f₁(z)+f₂(z)

На окружности C₁ :|-z₀|=R'₁ выполняется неравенство . Поэтому, дробь 1/(-z) можно представить в виде

Проведя почленное интегрирование, что возможно в силу равномерной сходимости ряда по переменной  на C₁

,

где введено обозначение

, n>0.

На окружности C₂:|-z₀|=R'₂ выполняется неравенство. Поэтому, дробь 1/(-z) можно представить в виде

В результате почленного интегрирования этого ряда получим:

,

где введено обозначение

Изменив направление интегрирования, получим:

, n>0

Подынтегральные функции в выражениях для c_n и c_-n являются аналитическими в круговом кольце R₂<|z-z₀|<R_1.. Поэтому в силу теоремы Коши значения соответствующих интегралов не изменится при произвольной деформации контуров интегрирования в области аналитичности подынтегральных функций. Это позволяет записать общее выражение

, n=0,1,2,…

где C - произвольный замкнутый контур, лежащий в кольце R₂<|z-z₀|<R₁ и содержащий точку z₀ внутри. Для f(z) окончательно можно записать:

f(z)=.

Т.к. z - произвольная точка внутри кольца R₂<|z-z₀|<R₁  ряд сходится к f(z) всюду внутри данного кольца, причем в замкнутом кольце R₂<R'₂|z-z₀|R'₁<R₁ ряд сходится к f(z) равномерно.

Докажем единственность разложения в ряд Лорана. Предположим, что имеет место другое разложение f(z)= , где хотя бы один коэффициент c'_nc_n. Тогда всюду внутри кольца R₂<|z-z₀|<R₁ имеет место равенство: =

Проведем окружность C_R , радиуса R: R ₂<R<R₁ , с центром в точке z₀ . Тогда ряды и сходятся на C_R равномерно.

Умножим оба ряда на (z-z₀)^-m-1 , где m- произвольное целое число и проинтегрируем почленно по окружности C_R.

Рассмотрим .

Т.о. для  m c'_m=c_m.

Примеры. Разложить в ряд Лорана с центром в

1. ,

2. ,

2. Ряд Лорана в окрестности бесконечно удаленной точки.

Определение. Степенной ряд вида , сходящийся во круговом кольценазываетсярядом Лорана в окрестности бесконечно удаленной точки.

Внимание. Главной частью ряда Лорана в окрестности называется, арегулярной (все наоборот).

Чтобы разложить функцию f(z) в ряд Лорана в окрестности нужно выполнить замену переменнойи провести разложение функциив ряд Лорана с центром в точке. Выполнив обратную замену переменной, получим искомый ряд Лорана в окрестности.

Пример.

Разложить в ряд Лорана с центром .

Ряд Лорана содержит только регулярную часть.