
Ильин / 17. Поверхности второго порядка
.pdf
17. Поверхности второго порядка
1 из 23
Рассматриваются простейшие поверхности второго порядка и их сечения.
2 из 23
17.1. Эллипсоиды
Рассмотрим на каноническое уравнение эллипсоида
2 |
|
2 |
|
2 |
|
(17.1) |
|
2 + 2 |
+ 2 |
= 1. |
|||||
|
|||||||
Координатные плоскости – плоскости симметрии, начало координат – центр симметрии. В силу неотрицательности слагаемых в левой части выполняются неравенства
| | ≤ ; | | ≤ ; | | ≤ .
Эллипсоид располагается внутри параллелепипеда с гранями параллельными координатным плоскостям
3 из 23

Рис. 17.1. Эллипсоид
4 из 23
Будем рассматривать сечения (эллипсоида) плоскостями
= ; = ; = . |
(17.2) |
Подставим z = h в уравнение эллипсоида
2 |
|
2 |
|
2 |
|
(17.3) |
|
2 + 2 |
+ 2 |
= 1. |
|||||
|
|||||||
Получим |
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
+ |
|
2 |
|
|
= 1. |
|
|
|
|
2 |
|
|
|
2 |
||
|
( √1 − |
2 |
( √1 − |
2 |
(17.4) |
|||||
|
) |
|
) |
|||||||
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||
Получили уравнение эллипса с полуосями
5 из 23

= √1 − |
2 |
; = √1 − |
2 |
. |
(17.5) |
|
2 |
2 |
|||||
|
|
|
|
Линии пересечения эллипсоида плоскостями - эллипсы. Частные случаи. Эллипсоид вращения - = . И сфера - =
= =
6 из 23
17.2. Гиперболоиды
Существуют два вида гиперболоидом. Однополостный гиперболоид задается уравнением
2 |
|
2 |
|
2 |
|
(17.6) |
|
2 + 2 |
− 2 |
= 1. |
|||||
|
|||||||
Вновь рассмотрим сечение плоскостью ортогональной оси Oz. Уравнение линии
|
2 |
|
|
+ |
|
2 |
|
|
= 1. |
|
|
|
|
2 |
|
|
|
2 |
|||
( √1 + |
2 |
( √1 + |
2 |
(17.7) |
||||||
) |
|
) |
||||||||
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|||
Это эллипс полуоси которого увеличиваются по мере удаления плоскости сечения от координатной плоскости xOy.
7 из 23
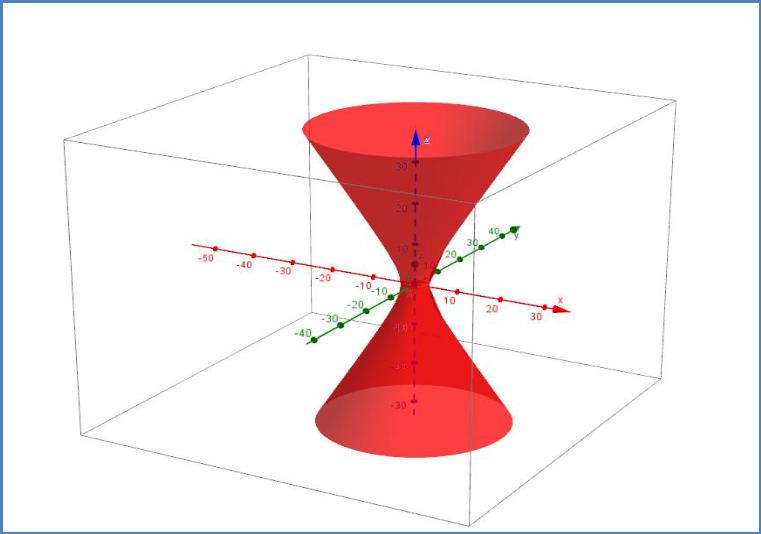
Рис. 17.2.Однополостный гиперболоид
8 из 23
В сечениях перпендикулярных осям Ox и Oy, соответственно получаем следующие уравнения линий
|
2 |
|
|
− |
|
2 |
|
|
= 1. |
|
|
|
|
2 |
|
|
|
2 |
|||
( √1 + |
2 |
( √1 + |
2 |
|||||||
) |
|
) |
|
|||||||
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
− |
|
2 |
|
|
= 1. |
|
|
|
|
2 |
|
|
|
2 |
|||
( √1 + |
2 |
( √1 + |
2 |
|||||||
) |
|
) |
|
|||||||
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|||
Координатные плоскости определяют сечения
2 |
2 |
2 |
2 |
||||
|
− |
|
= 1; |
|
− |
|
= 1. |
2 |
2 |
2 |
2 |
||||
(17.8)
(17.9)
(17.10)
9 из 23
Двуполостный гиперболоид задается каноническим уравне-
нием |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
(17.11) |
|
2 + 2 |
− 2 |
= −1. |
||||
|
|
||||||
Если в сечениях перпендикулярных оси Oz вновь получаем эллипс
|
2 |
|
2 |
|
||||||
|
|
|
|
+ |
|
|
|
|
= 1, |
|
|
|
|
2 |
|
|
|
2 |
|||
( √ |
2 |
|
( √ |
2 |
|
(17.12) |
||||
− 1) |
− 1) |
|||||||||
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|||
10 из 23
