
Ильин / 16. Линии второго порядка
.pdf16.8.Алгоритм упрощения уравнения
центральной линии второго порядка
Приведение центральной линии второго порядка ( 2 ≠ 0) к каноническому виду реализуется по следующему алгоритму.
Путем параллельного переноса начала координат приведем уравнение линии в виду (16.23)
Если 12 = 0, то оставим систему без изменений Если 12 ≠ 0, то перейдем к новой повернутой системе коор-
динат, вычисляя угол поворота (16.25) и используя формулы (16.18) для вычисления коэффициентов уравнения в новой (повернутой) системе координат.
В обоих случаях уравнение произвольной центральной линии в этой системе координат примет вид
21 из 32
" |
"2 + " |
|
"2 |
+ |
3 |
= 0. |
(16.27) |
22 |
|
||||||
11 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Далее всегда будем полагать, что 1 > 0.
Теорема 16.2. Пусть уравнение (16.11) линии эллиптического типа ( 2 > 0) нормировано так, что 1 > 0. Тогда при 3 < 0 это уравнение представляет собой эллипс, При 3 = 0 уравнению (16.11) удовлетворяют только координаты одной точки (вырожденный эллипс). При 3 > 0 уравнению (16.11) не удовлетворяют координаты ни какой точки (мнимый эллипс).
22 из 32
Теорема 16.3. Уравнение линии (16.11) гиперболического типа ( 2 < 0) при 3 ≠ 0 представляет собой гиперболу. При3 = 0 – пару пересекающихся прямых.
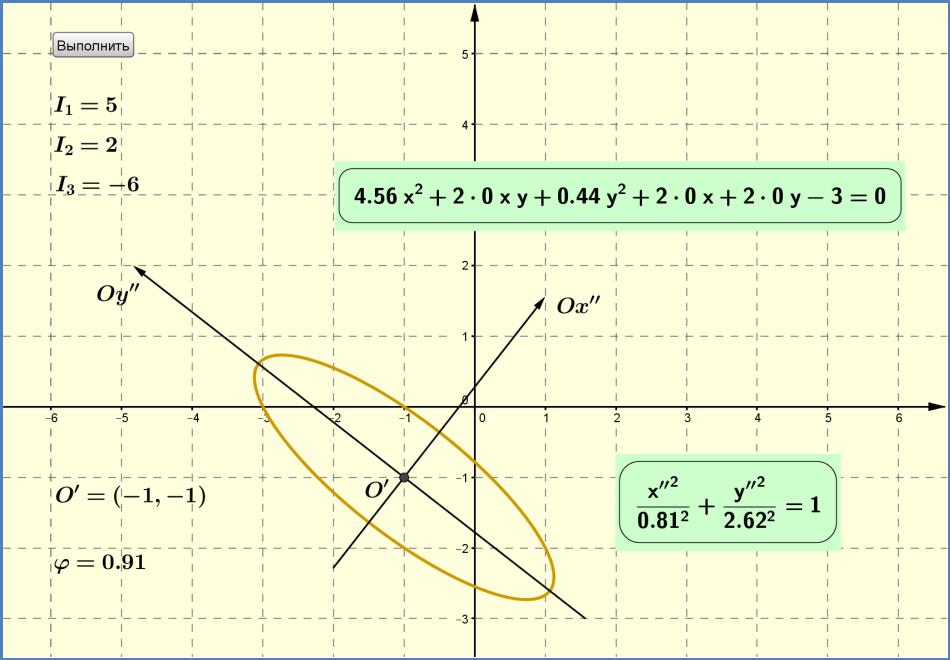
Пример 16.1. Привести к каноническому виду общее уравнение прямой второго порядка
2 2 + 4 + 3 2 + 8 + 10 + 6 = 0.
Решение. Будем следовать алгоритму (см. рис. далее).
23 из 32

24 из 32

25 из 32
26 из 32
16.9.Алгоритм упрощения уравнения линии
второго порядка параболического типа
Выполним стандартное упрощение.
Если 12 = 0, то оставим систему координат без изменений (без поворота). В противном случае перейдем к повёрнутой системе координат, определяя угол поворота по (16.25), а сами коэффициенты по (16.18). Уравнение линии примет вид
|
1′2 + 2 ′13 ′ + 2 ′23 ′ + 33 = 0. |
(16.28) |
||||||
Для определенности положили, что ′22 = 1 ≠ 0. |
|
|||||||
Далее выделим полный квадрат |
|
|
|
|
||||
|
|
′ |
2 |
′ |
2 |
|
|
|
1 |
(′ + |
23 |
) |
+ 2 ′13 ′ + 33 − |
23 |
|
= 0. |
(16.29) |
|
1 |
|
||||||
|
|
1 |
|
|
|
|
||
27 из 32
Перейдем к новой системе координат путем параллельного
переноса |
|
|
|
′′ = ′; ′′ = ′ + |
′23 |
|
|
|
. |
(16.30) |
|
|
|||
|
1 |
|
|
Определяя коэффициенты выражениями
′′13 = ′13; ′′23 |
= 33 |
− |
′23 |
2 |
, |
(16.31) |
1 |
|
|||||
|
|
|
|
|
|
|
получаем искомое уравнение |
|
|
|
|
|
|
1′′2 + 2 ′′13 ′′ + ′′33 = 0. |
|
|
(16.32) |
|||
28 из 32
Теорема 16.4. Уравнение линии (16.11) параболического типа ( 2 = 0) при 3 ≠ 0 представляет собой параболу. При 3 = 0 – либо пару параллельных действительных прямых (которые могут быть слившимися), либо пару мнимых прямых.
Пример 16.2. Привести к каноническому виду общее уравнение прямой второго порядка
2 2 + 4 + 8 2 + 8 + 10 + 6 = 0.
Решение. Будем следовать алгоритму (см. рис. далее).
29 из 32

30 из 32
