12.8. Нормированное уравнение прямой

Рассмотрим произвольную прямую (см. рис. 12.5). Опустим из начала координат на прямую перпендикуляр. Пусть P – точка пересечения перпендикуляра с прямой. На перпендикуляре выберем единичный вектор (нормаль к прямой) ̅ = (, ), направление которого совпадает с направлением

отрезка , длины .

22 из 33

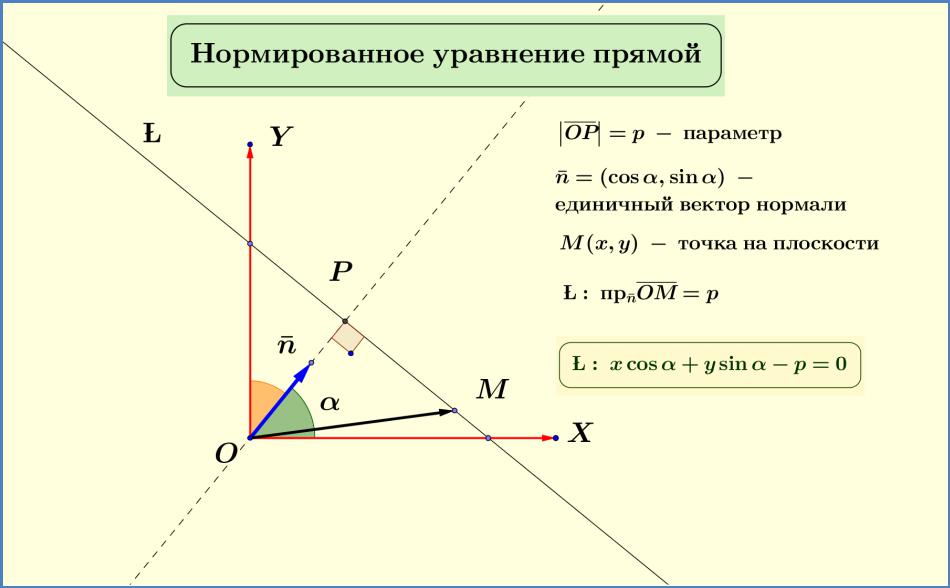
Рис. 12.5. Нормированное уравнение прямой

23 из 33

Пусть точка (, ) - произвольная точка прямой . Тогда эта точка принадлежит рассматриваемой прямой тогда и

только тогда, когда проекция вектора на ось, определяемую вектором ̅ равна или

пр̅ = .

Левую часть этого выражения можно записать в виде

пр̅ = ( ̅, ) = + .

Таким образом получаем уравнение

- нормированное уравнение плоскости.

Замечание. Поскольку углы и в сумме составляют прямой угол, то выполняется = . Поэтому нормированное уравнение прямой часто записывают в виде

24 из 33

Замечание. Для того, чтобы привести общее уравнение прямой к нормированному виду, достаточно учесть тот факт, что сумма квадратов направляющих косинусов равна единице. Поэтому умножим общее уравнение прямой (12.8) на нормирующий множитель

1

± √2 + 2,

знак перед которым выберем противоположным знаку С: по смыслу расстояние p неотрицательно.

Пример 12.2. Записать нормированное уравнение прямой, заданной каноническим уравнением

25 из 33

Решение. Преобразуем уравнение к общему виду

+ 3 − 10 = 0.

Для приведения уравнения к нормированному виду умножим

26 из 33