2.2.4 Гамма-распределение
f(t) t 1 e t
Г( )
Г(α) = (α - 1)!
При k k 2 ... n
k |
t k 1 |
exp( t) |
f (t) 0 |
|
|
(k 1)! |
0 |
|
|
||
λ0 – интенсивность отказов отдельных элементов;
k– число отказов, приводящих к отказу системы
Гамма-распределение
f(t) t 1 e t
Г( )
Г(α) = (α - 1)!
При k k 2 ... n
k |
t k 1 |
exp( t) |
f (t) 0 |
|
|
(k 1)! |
0 |
|
|
||
λ0 – интенсивность отказов отдельных элементов;
k– число отказов, приводящих к отказу системы
Г ( ) t 1e t dt
0
Для целых положительных чисел Г(α) = (α-1)!
Время до отказа подчин. Γ-распред., если отказ происходит при
накоплении отказов k элементов
2.2.5Распределение
Вейбулла
|
|
0 |
1 |
|
t ≥ |
|
t |
t |
|||
|
e |
|
0 |
||
f ( t ) = |
|
|
|
t 0 |
|
λ – параметр масштаба, α – параметр формы
Вероятность безотказной работы и интенсивность отказов при распределении Вейбулла
•P(t) = exp ( - λ ∙ t α )
•При α < 1 λ(t) убывает
α> 1 λ(t) возрастает
α= 1 λ = const , т. е. получ.
экспоненц. распределение
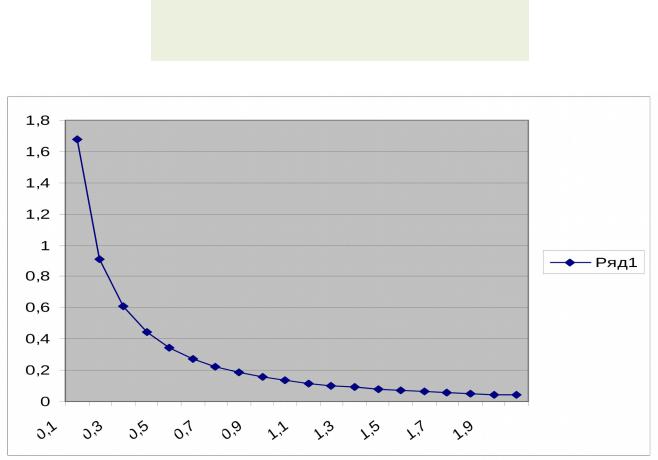
Графики функций плотности вероятности распределения Вейбулла
α = 0.5; λ = 2
Графики функций плотности вероятности распределения Вейбулла
α = 0.6 λ = 1
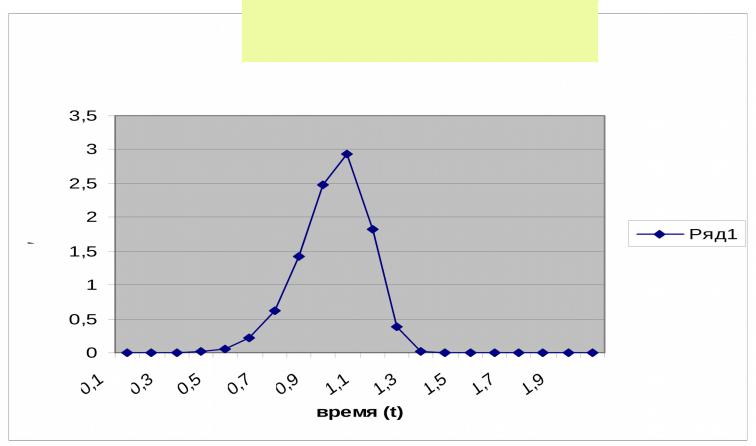
Графики функций плотности вероятности распределения Вейбулла
α =8; λ = 1
Графики функций плотности вероятности распределения Вейбулла
α |
=2; λ= |
1 |
|
2.2.6Распределение χ2
x = χ2
f 2 |
(1/ 2)k / 2 |
x( |
k |
1)e x / 2 |
|
2 |
при x > 0 |
||||
|
Г (k / 2) |
|
|
|
|
Распределение χ 2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых случайных величин, каждая из которых подчинена нормальному закону с математическим
ожиданием равным нулю.