11.5. Гамма-распределение.

В самом общем виде этот закон характеризуется плотностью вероятности вида

; (11.24)

здесь Г(α) – гамма-функция; Г(α) = .

Для целых положительных значений α= k; k = 0; 1, 2, …n

Г(α) = (α – 1)! (11.25)

Тогда из выражения (11.24) получается плотность распределения времени до отказа, который происходит в оборудовании при накоплении отказов k элементов, каждый из которых отказывает по экспоненциальному закону:

, (11.26)

где λ₀ – интенсивность отказов отдельных элементов;

k– число отказов, приводящих к отказу оборудования.

При k = 1 формула (11.26) дает экспоненциальное распределение:

. (11.27)

11.6. Закон распределения Вейбулла.

(11.28)

Плотность этого распределения имеет вид

(11.28)

где α называют параметром формы, а λ – параметром масштаба [2].

Наличие этих двух параметров делает закон Вейбулла очень удобным для подбора подходящего выражения функции f(t), наиболее приближающего модель к опытному распределению.

Рассматриваемое распределение Вейбулла хорошо описывает функцию надежности изделий со скрытыми дефектами. При α > 1 этот закон подходит для описания функции надежности быстро стареющих изделий.

Известно также, что многие интегральные микросхемы имеют распределение наработки до отказа по Вейбуллу с показателем α < 1.

Из приводимых ниже графиков функций f(t) вейбулловского распределения ясно видно, что при различных значениях параметра α этот закон приближается то к нормальному, то к экспоненциальному.

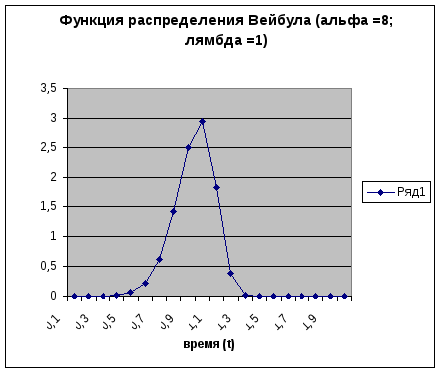
Рис.. 11.2. Графики функций распределения Вейбулла

11.7. Обобщение различных непрерывных распределений.

Выдающийся английский математик и философ Карл Пирсон предложил общую форму

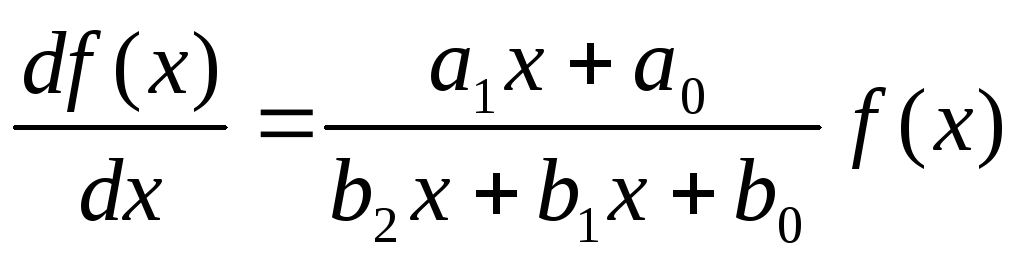, (11.29)

из которой, в зависимости от значений параметров a_i, b_i , получаются то Гамма-распределение, то распределение Стьюдента, то Гаусса и др.

Связь различных законов иллюстрируется, например, тем, что при подстановке в формулу Г-распределения α = n /2, λ = 0,5 получается χ² - распределение с n степенями свободы.

При α = 2 из распределения Вейбулла получается распределение Рэлея:

. (11.30)

Интересно, что закон Рэлея можно получит и из распределения случайной величины

, (11.31)

то есть χ-распределения при n =2.

Литература

1. Вентцель Е.С. Теория вероятностей. М.: Наука, 1964. – 576 с.

2. Острейковский В.А. Теория надежности: Учебник для вузов. М.: - Высш. шк., 2008. - 463 с.